2020年10月18日日志

课后回顾(重点）

1.第一篇
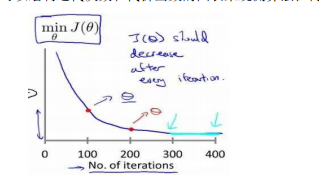
梯度下降算法的每次迭代受到学习率的影响：
如果学习率𝑎过小，则达到收敛所需的迭代次数会非常高；
如果学习率𝑎过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。
考虑的学习率：
𝛼 = 0.01，0.03，0.1，0.3，1，3，10

2.flipup/flipud 表示向上/向下翻转。
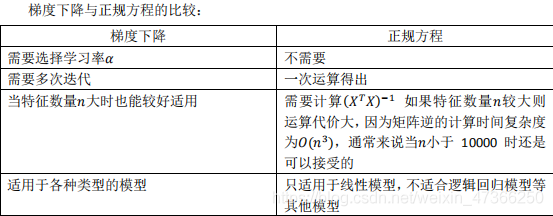
矩阵的逆矩阵，键入 pinv(A)，通常称为伪逆矩阵，矩阵 𝐴 求逆，因此这就是 𝐴矩阵的逆矩阵。
设 temp = pinv(A)，然后再用𝑡𝑒𝑚𝑝 乘以𝐴，这实际上得到的就是单位矩阵，对角线为 1，其他元素为 0

3.第二篇

1.实现一个神经网络时，通常不直接使用for循环遍历整个训练集

2.神经网络的计算：前向传播+反向传播

3.逻辑回归模型：适用于二分类的算法

二分类问题：习得一个分类器，以图片的特征向量作为输入，预测输出结果y为1还是0

𝑋是一个规模为𝑛𝑥乘以𝑚的矩阵；

X.shape 等于(𝑛𝑥, 𝑚)

𝑌等于𝑦(1)… 𝑦(𝑚)

Y.shape 等于(1, 𝑚)

让𝑦^ 表示 𝑦 等于 1 的一种可能性或者是机会，前提条件是给定了输入特征𝑋。

换句话来说，如果𝑋是我们在上个视频看到的图片，你想让𝑦^来告诉你这是一只猫的图片的机率有多大。在之前的视频中所说的

𝑋是一个𝑛𝑥维的向量（相当于有𝑛𝑥个特征的特征向量）

𝑤来表示逻辑回归的参数，这也是一个𝑛𝑥维向量（因为𝑤实际上是特征权重，维度与特征向量相同）

参数里面还有𝑏，这是一个实数（表示偏差）。

所以给出输入𝑥以及参数𝑤和𝑏之后，我们怎样产生输出预测值𝑦^{，一件你可以尝试却不可行的事是让𝑦}= 𝑤𝑇𝑥 + b

4.逻辑回归的代价函数

损失函数是在单个训练样本中定义的

算法的代价函数是对𝑚个样本的损失函数求和然后除以m

4.第三篇