机器学习-交叉熵、信息熵、相对熵、KL散度、交叉熵损失等函数讲解

熵

熵，是一个物理学概念，它表示一个系统的不确定性程度，或者说是一个系统的混乱系统

信息熵

• n:表示随机变量可能的取值(i=1,2,…n)
• x:表示随机变量
• P(x):表示随机变量x的概率函数

举一个生动的小例子：
班花A从5位同学里挑选男朋友，宿舍1中全是帅哥，班花B在宿舍2中只有一个是帅哥。
问题来了：班花A和班花B，那个班花在选择时，大脑更乱？

从对选择每个人的概率中，由信息熵公式可得两位班花的大脑混乱程度。

由此可知，班花A的大脑更混乱，因为全是帅哥，不知道选择哪一个。而班花B呢，只有一个帅哥可以选择，也别无选择。无论是log以10为底，还是log以2为底、还是e为底，对结果都一样，都是班花A高。

相对熵、KL散度

相对熵=KL散度
KL散度=相对熵

KL散度：是两个概率分布间差异的非对称性度量。
通俗说法：KL散度是用来衡量同一个随机变量的两个不同分布之间的距离。

KL散度公式：

特性：

• 非对称性
• 非负性

举个小例子：
两个班级对三位同学谁是校花进行概率估计

根据KL散度公式计算

再使用信息熵计算

KL散度公式变形：

交叉熵

交叉熵主要应用：主要用于度量同一个随机变量x的预测分布Q与真实分布P之间的差距

交叉熵=KL散度(相对熵)+信息熵

交叉熵公式：
其中q(x)为概率，q(x)为真实标签值(正确为1，错误为0)


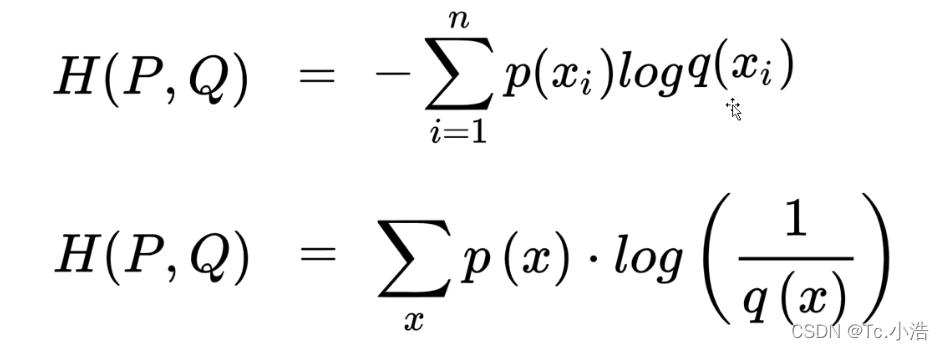
结论：预测越准确，交叉熵越小
交叉熵只跟真实标签的预测概率值有关q(x)

最简公式：

交叉熵的二分类公式：

普通公式，最简公式、二分类公式，计算只有两种分类的情况下，结果一样吗？我们通过下面的例子可以得出，结果是一致的

为什么在很多的网络模型中，使用交叉熵做损失函数而不使用KL散度做损失函数呢？

softmax

• 将数字转换成概率的神器
• 进行数据归一化的利器