论文导读 | 大语言模型与知识图谱复杂逻辑推理

前 言

大语言模型，尤其是基于思维链提示词（Chain-of Thought Prompting）[1]的方法，在多种自然语言推理任务上取得了出色的表现，但不擅长解决比示例问题更难的推理问题上。本文首先介绍复杂推理的两个分解提示词方法，再进一步介绍将提示词方法应用于知识图谱复杂逻辑推理的工作。

文章一：“Least-to-Most Prompting”[2]

让大模型学会处理更复杂的推理

本文首先提出了Least-to-Most Prompting方法的动机，是人类智慧与机器学习之间的三个差异：

（1）面对一个新问题时，人类可以通过很少的示例中解决它，但机器通常需要大规模的标注语料；

（2）人类可以很清楚的阐释所做预测的隐含原因，但机器学习是一个黑盒子；

（3）人类可以解决比之前见过的问题更难的问题，但机器学习只能解决与之前相同难度的问题。

Google Brain在2022年提出Chain-of-Thought方法，利用few-shot prompting尝试填补人类智慧和机器学习之间的差距，但他不能解决比实例问题更难的问题。为此，该团队提出了Least-to-Most Prompting方法，该方法分为两个阶段：第一阶段将一个复杂问题分解为一个简单子问题序列；第二阶段按顺序解决子问题，且回答后续子问题会依赖前序子问题的答案。

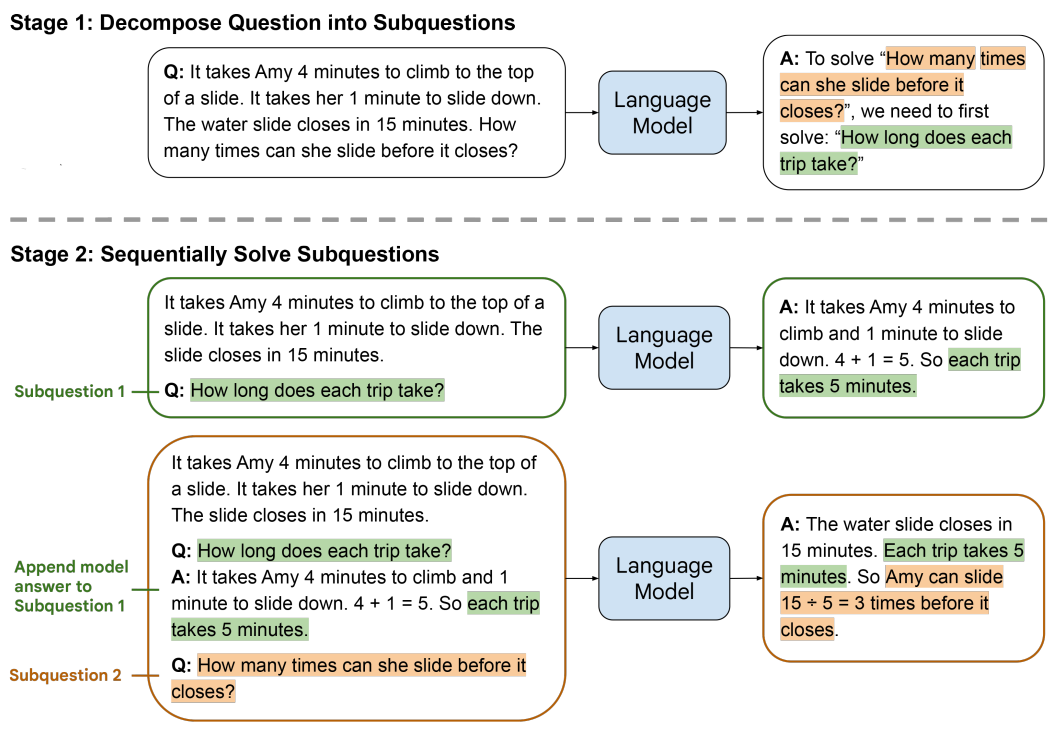
下图给出了Least-to-Most Prompting方法解决一个数学问题的示例：

（1）将复杂问题分解为简单子问题；

（2）按序解决子问题，其中，回答第二个子问题时使用了第一个子问题的答案。

实验部分，论文通过符号操作（symbolic manipulation）、组合泛化（compositional generalization）和数学推理（math reasoning）三类任务来验证Least-to-Most Prompting的效果，并与Chain-of-Thought Prompting方法进行比较。

符号操作任务的输入是一个单词列表，对应输出是将这个单词列表中所有单词最后一个字母连接起来。如，“thinking machine”的输出为“ge”。

如图，Least-to-Most Prompting方法首先将一个长的单词序列转化为子序列，