本文详细探讨了反函数的概念，强调了导数在验证反函数存在性和求解反函数导数中的作用。特别指出，虽然导数为0的函数可能不符合水平线检验，但某些函数如正切函数仍然有反函数。同时，介绍了反三角函数如反正弦、反余弦、反正切等的定义、图像、导数推导及其限制定义域的重要性。通过实例展示了反三角函数的导数计算，并讨论了它们在满足特定条件下的性质和应用。
Chapter10：反函数和反三角函数
10.反函数和反三角函数
10.1 导数和反函数
10.1.1 使用导数证明反函数存在
如果满足水平线检验，则一个函数是否存在反函数
（一个
y
y
y 对应一个
x
x
x）
此方法的大体思想是：在一定区间内，如果函数单增或单减，函数图像必然与每条水平线只相交一次（即符合水平线检验），由此得出：存在该函数的反函数
10.1.2 用导数检验函数是否反函数：可能会出现问题
下面的分段函数满足
f
′
(
x
)
≥
0
f'(x) \geq 0
f′(x)≥0 ，符合水平线检验，不存在其反函数
问题：
导数为0的原函数表现为平行于
x
x
x 轴，此部分与水平线相交点多于一次，显然不符合水平线检验（即此原函数不存在其反函数），但有些不符合水平线检验的函数，也存在其对应的反函数
下图为 y = t a n ( x ) y=tan(x) y=tan(x) 不符合水平线检验（意味着不存在其反函数）
但 y = t a n ( x ) y=tan(x) y=tan(x) 的反函数存在，其为 y = a r c t a n ( x ) y=arctan(x) y=arctan(x)
综上：当函数有不连续点或垂直渐近线时，用导数判断函数是否存在反函数的方法不再适用
问题的根源其实在于正切函数定义域不在一起，而上面提到的判断方法其定义域是在一起的。
问题的解决：
导数证明反函数存在的方法的使用条件：应该限制定义域
10.1.3 求反函数的导数
f − 1 ( x ) ≠ ( f ( x ) ) − 1 f^{-1}(x) \neq (f(x))^{-1} f−1(x)=(f(x))−1 ，前者代表反函数，而后者代表函数的倒数
f 2 ( x ) = ( f ( x ) ) 2 f^2(x)=(f(x))^2 f2(x)=(f(x))2 ，两者都代表函数的平方
如果原函数处处可导，其反函数不一定处处存在
求反函数的导数的例子
例1：
例2：
例3：
10.2 反三角函数
反三角函数中的 ar 代表 arc（弧）【详见本人另一博客中 2.2 描述的三角函数的定义】
反双曲函数中的 ar 代表 area（面积）【详见本人另一博客中 9.7.0 描述的对双曲函数的定义】
10.2.1 反正弦函数【 y=arcsin(x) 】
y
=
s
i
n
(
x
)
y=sin(x)
y=sin(x)
水平线与函数图像相交多次，不满足水平线检验，接下来通过限制定义域来使其满足水平线检验
将上图中的实线做关于
y
=
x
y=x
y=x 的图像，得到该定义域内的反函数，即
s
i
n
−
1
(
x
)
=
a
r
c
s
i
n
(
x
)
sin^{-1}(x)=arcsin(x)
sin−1(x)=arcsin(x)
满足水平线检验的
s
i
n
(
x
)
sin(x)
sin(x) 的定义域
[
−
π
2
，
π
2
]
[-\frac{\pi}{2}，\frac{\pi}{2}]
[−2π，2π]，值域
[
−
1
,
1
]
[-1,1]
[−1,1]
其反函数
a
r
c
s
i
n
(
x
)
arcsin(x)
arcsin(x) 的定义域
[
−
1
,
1
]
[-1,1]
[−1,1]，值域
[
−
π
2
，
π
2
]
[-\frac{\pi}{2}，\frac{\pi}{2}]
[−2π，2π]
反正弦函数的图像
y
=
s
i
n
−
1
(
x
)
=
a
r
c
s
i
n
(
x
)
y=sin^{-1}(x)=arcsin(x)
y=sin−1(x)=arcsin(x)
反正弦函数的导数推导
例1：
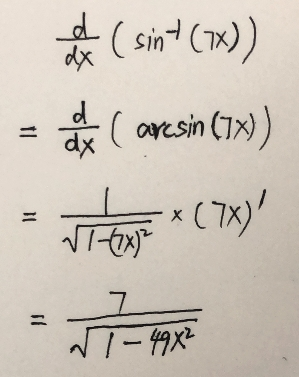
例2：
10.2.2 反余弦函数【 y=arccos(x) 】
y
=
c
o
s
(
x
)
y=cos(x)
y=cos(x)
水平线与函数图像相交多次，不满足水平线检验，接下来通过限制定义域来使其满足水平线检验
将上图中的实线做关于
y
=
x
y=x
y=x 的图像，得到该定义域内的反函数，即
c
o
s
−
1
(
x
)
=
a
r
c
c
o
s
(
x
)
cos^{-1}(x)=arccos(x)
cos−1(x)=arccos(x)
反余弦函数的图像
y = c o s − 1 ( x ) = a r c c o s ( x ) y=cos^{-1}(x)=arccos(x) y=cos−1(x)=arccos(x)
反余弦函数的导数推导
证明：
a
r
c
s
i
n
(
x
)
+
a
r
c
c
o
s
(
x
)
=
π
2
arcsin(x)+arccos(x)=\frac{\pi}{2}
arcsin(x)+arccos(x)=2π
10.2.3 反正切函数【 y=arctan(x) 】
y
=
t
a
n
(
x
)
y=tan(x)
y=tan(x)
水平线与函数图像相交多次，不满足水平线检验，接下来通过限制定义域来使其满足水平线检验
将上图中的实线做关于 y = x y=x y=x 的图像，得到该定义域内的反函数，即 t a n − 1 ( x ) = a r c t a n ( x ) tan^{-1}(x)=arctan(x) tan−1(x)=arctan(x)
反正切函数的图像
y
=
t
a
n
−
1
(
x
)
=
a
r
c
t
a
n
(
x
)
y=tan^{-1}(x)=arctan(x)
y=tan−1(x)=arctan(x)
反正切函数的导数推导
10.2.4 反余切函数【 y=arccot(x) 】
y
=
c
o
t
(
x
)
y=cot(x)
y=cot(x)
水平线与函数图像相交多次，不满足水平线检验，接下来通过限制定义域来使其满足水平线检验
.
将上图中的实线做关于
y
=
x
y=x
y=x 的图像，得到该定义域内的反函数，即
c
o
t
−
1
(
x
)
=
a
r
c
c
o
t
(
x
)
cot^{-1}(x)=arccot(x)
cot−1(x)=arccot(x)
反余切函数图像
y
=
c
o
t
−
1
(
x
)
=
a
r
c
c
o
t
(
x
)
y=cot^{-1}(x)=arccot(x)
y=cot−1(x)=arccot(x)
反余切函数的导数推导
10.2.5 反正割函数【 y=arcsec(x) 】
y
=
s
e
c
(
x
)
y=sec(x)
y=sec(x)
水平线与函数图像相交多次，不满足水平线检验，接下来通过限制定义域来使其满足水平线检验
将上图中的实线做关于 y = x y=x y=x 的图像，得到该定义域内的反函数，即 s e c − 1 ( x ) = a r c s e c ( x ) sec^{-1}(x)=arcsec(x) sec−1(x)=arcsec(x)
反正割函数图像
y = s e c − 1 ( x ) = a r c s e c ( x ) y=sec^{-1}(x)=arcsec(x) y=sec−1(x)=arcsec(x)
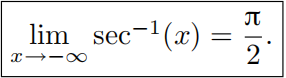
反正割函数的导数推导
10.2.6 反余割函数【 y=arccsc(x) 】
y
=
c
s
c
(
x
)
y=csc(x)
y=csc(x)
水平线与函数图像相交多次，不满足水平线检验，接下来通过限制定义域来使其满足水平线检验
将上图中的实线做关于 y = x y=x y=x 的图像，得到该定义域内的反函数，即 c s c − 1 ( x ) = a r c c s c ( x ) csc^{-1}(x)=arccsc(x) csc−1(x)=arccsc(x)
反余割函数图像
y
=
c
s
c
−
1
(
x
)
=
a
r
c
c
s
c
(
x
)
y=csc^{-1}(x)=arccsc(x)
y=csc−1(x)=arccsc(x)
反余割函数的导数推导
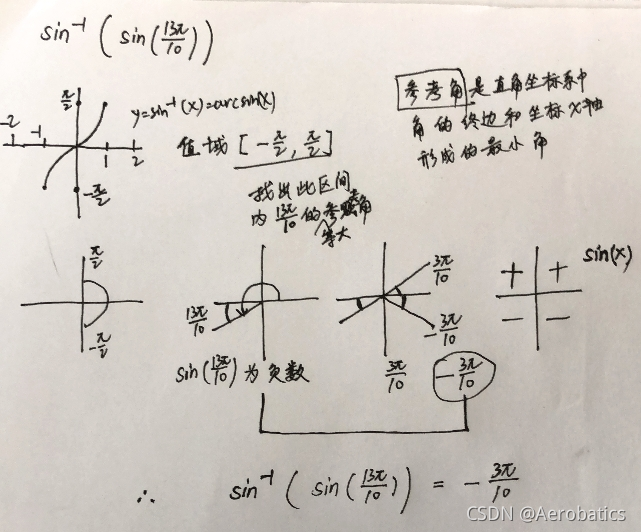
10.2.7 计算反三角函数
例子：
扫一扫
3089
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
