数列和级数（基本概念）

22.数列和级数（基本概念）

22.1 数列的收敛和发散

通项 $a_n$ 的极限存在

意味着 $a_n$ 在开始时可能有稍许徘徊，最后会越来越趋近于 $L$ 并保持这种趋势。
若存在这样的 $L$ ，则数列 { a n } \{a_n\} {an​} 收敛，否则发散

22.1.1 数列和函数的联系

数列继承了函数的极限性质

1.数列的和、差、积、商
两个收敛数列 { a n } \{a_n\} {an​} 和 { a n } \{a_n\} {an​}，当 $n\to 0$ 时，$a_n\to L，b_n\to M$，则其和 $a_n+b_n$ 构成一个收敛于 $L+M$ 的新数列。对于差、积、商和常数的积同样适用

2.夹逼定理对数列也适用

若 $c_n\le a_n\le b_n$，且当 $n\to \infty$时，$b_n\to L，c_n\to L$，则当 $n\to \infty$ 时，$a_n\to L$

例子：

3.连续函数保持极限

假设当 $n\to \infty$ 时 $a_n\to L$，则如果函数 $f$ 在 $x=L$ 连续，我们说当 $n\to \infty$ 时 $f(a_n)\to f(L)$

例子：

4.洛必达法则应用于数列

注意：数列中 $n$ 为整数，所以不能对关于 $n$ 的量 $a_n$ 求导

函数求导的目的：当对函数 $f$ 求关于变量 $x$ 的导数时，只是为了看一下当对 $x$ 做极小变动时函数 $f(x)$ 有什么变化

不能对数列中 $n$ 做极小变动，因为极小变动后它就不是整数了

解决办法：找出数列对应的函数，先对函数应用洛必达法则，求出极限值，再求得 $$\underset{n\to \infty }{\lim }{a}_n$$

例子：

22.1.2 两个重要数列

常见数列极限

22.1.2.1 第一个数列

等比数列通项，其中 $r$ 为公比
$$a_n=r^n$$

等比数列，首项从 $a{r}^0=a$ 开始
$$a_n=a{r}^n$$

22.1.2.2 第二个数列

22.2 级数的收敛与发散

无穷数列

无穷级数

为理解级数的极限，构造部分和数列

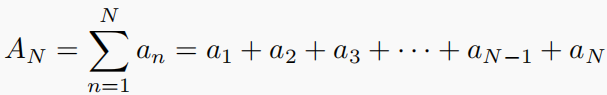
22.2.1 几何级数（理论）

22.3 第 n 项判别法（理论）

大白的目的：控制每一步的步长（$a_n$）最终使自己到达极限位置（要求要走很多步）

例子：

第 $n$ 项判别法的注意事项：

1.第 $n$ 项判别法不能用于级数收敛性的判别！
2.只有当数列通项 ($a_n$) 的极限不为0时，才可使用第 n 项判别法
3.第 $n$ 项判别法告诉我们，任何公比不在 $(-1,1)$ 里的几何级数均发散

22.4 无穷级数和反常积分的性质

反常积分的四个判别法对无穷级数仍适用

22.4.1 比较判别法（理论）

两个不同数列之间（区别于比式判别法的同一个数列的相邻项）

例子：

22.4.2 极限比较判别法（理论）

例子：

22.4.3 p判别法（理论）

与反常积分的p判别法一样（只是这里将积分符号换为了求和符号）

例子：
$$\sum _{n=1}^{\infty }\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}$$

例子：

调和级数（p=1）

22.4.4 绝对收敛判别法

例1：

例2：

22.5 级数的新判别法

22.5.1 比式判别法（相邻项的比）（达朗贝尔判别法）

同一个数列的相邻项（区别于比较判别法的两个不同数列间）

例子：

22.5.2 根式判别法（第n项绝对值的n次方根）（柯西判别法）

22.5.3 积分判别法（级数与积分比较）（柯西积分审敛法）

22.5.4 交错级数判别法（莱布尼茨判别法）

例子：

条件收敛

例子：

例子：

22.6 总结