动目标显示（MTI）,多脉冲对消仿真

最新推荐文章于 2023-12-14 17:05:58 发布

学习小混子

最新推荐文章于 2023-12-14 17:05:58 发布

阅读量4.1k

点赞数 17

分类专栏：雷达信号处理基础知识文章标签： matlab 信号处理

本文链接：https://blog.csdn.net/weixin_48627103/article/details/129802384

版权

雷达信号处理基础知识专栏收录该内容

3 篇文章 1 订阅

订阅专栏

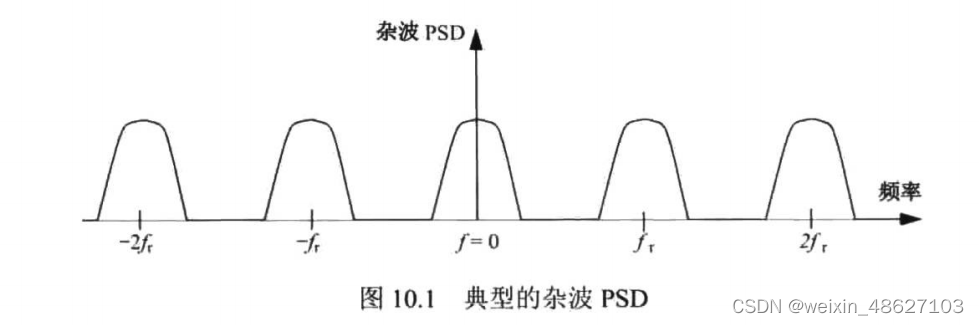
杂波频谱一般集中在 $DC(f=0)$ 和雷达 $PRFf_r$ 的整数倍周围，如图10.1(a)所示。在连续波雷达中，连续波雷达中，由于大多数杂波功率集中在零频带附近，通过忽略DC附近的接收机输出，
则可以避免杂波或将其抑制掉。脉冲雷达系统则可使用特殊的滤波器来将慢速运动（或固
定）目标与快速移动目标区分开来。这类滤波器称为动目标显示器(MTI)。简单地说，MTI
滤波器的目的就是抑制掉杂波所生成的像目标似的一些回波，并让动目标回波没有损失地
（或损失很小地）通过滤波器。为了有效地抑制掉杂波回波，MTI滤波器在DC和PF整数
倍处必须有一个很深的阻带。图10.2(b)给出了一个典型的MTI滤波器响应图，图10.2(c)
则给出了以图10.2(a)中的PSD为输入时的输出图。

MTI滤波器可以用延迟线对消器来实现。在本章的后面我们将证明，此类MTI滤波器
的频率响应是周期性的，零值在PRF的整数倍上。因此，多普勒频率等于听的目标会出现
很大衰减。由于多普勒频率与目标速度成正比( $f_d = 2v/\lambda$ ),所以产生多普勒频率为无整数
倍的目标速度称为盲速。更准确地说，

$\nu_{\mathrm{blind}}=(n\lambda f_{\mathrm{r}})/2;n\geqslant0$

单延迟线对消器可以用图10.3所示的方法来实现。对消器的脉冲响应表示为 $h(t)$ 。输
出y(t)等于脉冲响应 $h(t)$ 和输入 $x(t)$ 之间的卷积。由于单延迟线对消器在读出输出前需要有两
个不同的输入脉冲，因而经常称其为“双脉冲对消器”。

延迟T等于雷达的PRI。输出信号 y(t)为

$y(t)=x(t)-x(t-T)$

对消器的时域脉冲响应由下式给出：

$h(t)=\delta(t)-\delta(t-T)$

单延迟对消器响应为

$H(z)=1-z^{-1}$

单延迟线对消器的功率增益为：

$\left|H(\omega)\right|^2=4(\sin(\omega T/2))^2$

多延迟对消器可以由多个单延迟对消器级联而成，N脉冲对消的脉冲响应为、

$\operatorname{h}(\mathrm{t})=\sum_{\mathrm{n}=0}^\mathrm{N}\omega_\mathrm{n}\delta(\mathrm{t}-\mathrm{n}\mathrm{T}_\mathrm{r})$

式中，N为对消次数，注意一次对消需要两个脉冲，两次对消需要三个脉冲，以此类推，系数 $\omega_{\mathrm{n}}$ 为二项式系数，计算方式如下

$\omega_\mathrm{n}=(-1)^\mathrm{n}\mathrm{C}_\mathrm{N}^\mathrm{n}=(-1)^\mathrm{n}\frac{\mathrm{N}!}{(\mathrm{N-n})!\mathrm{n}!},\mathrm{n}=0,1,\ldots\ldots,\mathrm{N}$

关于MTI的仿真，从时域出发很简单写，就是用脉冲乘以加权系数然后求和，但是值得注意的是从时域对消后会少脉冲，二阶对消会少一个脉冲，三阶对消会少两个脉冲依次类推。利用matlab的filter函数，很容易实现MTI时域对消。

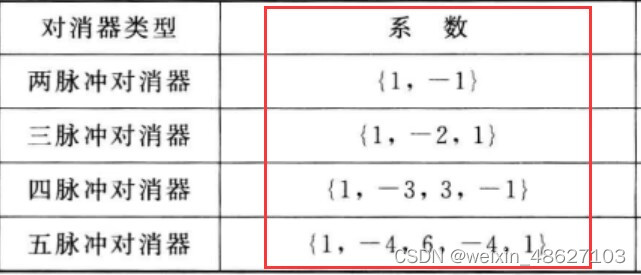
如上图，假设三阶对消，h为对消器系数，x为6个脉冲回波。通过函数filter函数可以看到，第一个脉冲是没有被滤波的，因此可以丢掉这个脉冲。下面是MTI时域实现代码

function [sum_PC_MTI] = MTI(sum_PC_Np,MTI_filter_n)
%功能：完成数据的MTI
%输入：
%sum_PC_Np:和通道信号
%MTI_filter_n:MTI脉冲对消个数
%输出：
%完成MTI之后的和通道信号
 switch MTI_filter_n %判断对消个数
     case 2
         h = [1,-1];    
     case 3
         h = [1,-2,1];
     case 4
         h = [1,-3,3,-1];
         
 end
  sum_PC_Np = filter(h,1,sum_PC_Np) ;%经过对消之后的矩阵
  sum_PC_MTI = sum_PC_Np(MTI_filter_n:end,:);%丢掉前MTI_filter_n个脉冲
end

下图是32个脉冲积累测速仿真MTI前后对比。

可以看到经过MTI后零频附近的静态杂波被对消掉了。但是当目标处于盲速或者速度很小接近于零时，也会被对消掉，这样就检测不出目标的速度了，如下图

目标速度处于盲速，多普勒频移在PRF的整数倍上，经过MTI滤波后被对消掉，无法测速。

后续可以通过设置多重频，解模糊来避免这个问题。

本人为初学者，很多地方可能理解有误！

参考《雷达系统matlab仿真第三版》

学习小混子

关注

17
点赞
踩
57

收藏

觉得还不错? 一键收藏
8
评论
动目标显示（MTI）,多脉冲对消仿真

关于MTI的仿真，从时域出发很简单写，就是用脉冲乘以加权系数然后求和，但是值得注意的是从时域对消后会少脉冲，二阶对消会少一个脉冲，三阶对消会少两个脉冲依次类推。如上图，假设三阶对消，h为对消器系数，x为6个脉冲回波。在连续波雷达中，连续波雷达中，由于大多数杂波功率集中在零频带附近，通过忽略DC附近的接收机输出，目标速度处于盲速，多普勒频移在PRF的整数倍上，经过MTI滤波后被对消掉，无法测速。式中，N为对消次数，注意一次对消需要两个脉冲，两次对消需要三个脉冲，以此类推，系数。对消器的脉冲响应表示为。
复制链接

扫一扫