求解线性方程组的数值方法matlab实现Gauss消去法、LU分解法、Jacobi迭代法、Gauss-Seidel迭代法，代码程序，理论分析，最基本的操作

方程根求解数值方法matlab实现二分法、牛顿法、斜截法

求解线性方程组的数值方法matlab实现Gauss消去法、LU分解法、Jacobi迭代法、Gauss-Seidel迭代法，代码程序，理论分析，最基本的操作

实验内容：

实验代码程序

1、Gauss消去法：
M文件：
function x = Gauss(A,b)
a=[A,b];
x=[];
n=length(a)-1;
for k=1:n
    for i=k+1:n
        c=a(i,k)/a(k,k);
        for j=k:n+1
            a(i,j)=a(i,j)-c*a(k,j)
        end
    end
end
x=take(a);

function x = take(a)
n=length(a)-1;
for i=n:-1:1
    s=0;
    if i==n
        x(i)=(a(n,n+1)-s)/a(n,n);
    else
        for j=n:-1:i
            s=s+a(i,j)*x(j);
        end
        x(i)=(a(i,n+1)-s)/a(i,i);
    end
end

主函数：
A=[2 1 -5 1;1 -3 0 1;2 0 -1 2;1 4 -7 3];
b=[-1;4;3;4];
Gauss(A,b)


2、LU分解法：
M文件：
（1）
function x=LU(A,b)
n=length(A)
A=[A b]
L=eye(n)
U=zeros(n)
for i=1:n-1
      for j=i:n-1
      L(j+1,i)=A(j+1,i)/A(i,i)
      A(j+1,:)=A(j+1,:)-L(j+1,i)*A(i,:)
      end
end
U=A(:,1:n)
a1=[L b]
y=zeros(n,1)
y=huidaini(a1)
a2=[U y]
x=huidai(a2)

（2）
function x = take(a)
n=length(a)-1;
for i=n:-1:1
    s=0;
    if i==n
        x(i)=(a(n,n+1)-s)/a(n,n);
    else
        for j=n:-1:i
            s=s+a(i,j)*x(j);
        end
        x(i)=(a(i,n+1)-s)/a(i,i);
    end
end

（3）
function x=take_ni(a)
n=length(a)-1;
x=zeros(n,1);
s=0;
for i=1:1:n
      if i==1
         x(1)=a(1,n+1)/a(1,1)
      else
            for j=1:1:i-1
                 s=s+a(i,j)*x(j)
            end
            x(i)=(a(i,n+1)-s)/a(i,i)
            s=0
      end
end

主函数：
A=[2 1 -5 1;1 -3 0 1;2 0 -1 2;1 4 -7 3];
b=[-1;4;3;4];
LU(A,b)


3、Jacobi迭代法：
M文件：
function Jacobi(A, b)
m=length(A);
L=tril(A, -1);
U=triu(A, 1);
D=diag( diag(A));
B=inv(D)*(-L-U);
g=inv(D)*b;
x0=zeros(m,1);
if (any(diag(A)==0))
    error('主对角线存在零元素，雅可比迭代法无法进行，程序终止')
end
eps=input( '输入误差限eps=');
N=input( '请输入最大允许的迭代次数N=');
k=0;
while k<=N
         x1=B* x0+g;
         k=k+1;
         fprintf( '第%2d次迭代的近似解为\n',k)
         disp(x1);
         if norm(x1-x0)<eps
            fprintf( '满足精度要求的方程组的近似解为\n')
            disp(x1);
            break
          end
          if k>N
             fprintf( '迭代次数超限\n' )
             break
          end
          x0=x1;
end
end

主函数：
A=[2 1 -5 1;1 -3 0 1;2 0 -1 2;1 4 -7 3];
b=[-1;4;3;4];
Jacobi(A,b)

4、Gauss-Seidel迭代法：
M文件：
function GS_iteration(A, b)
m=length(A);
L=tril(A,-1);
U=triu(A,1);
D=diag(diag(A));
B=inv(D+L)*(-U);
g=inv(D+L)*b;
x0=zeros(m,1);
if (any(diag(A)==0))
   error('主对角线存在零元素，高斯迭代法无法进行，程序终止' )
end
eps=input( '输入误差限eps=');
N=input( '请输入最大允许的迭代次数N=');
k=0;
while k<=N
         x1=B*x0+g;
         k=k+1;
         fprintf( '第%2d次迭代的近似解为\n',k)
         disp(x1);
         if norm(x1-x0)<eps
            fprintf('满足精度要求的方程组的近似解为\n')
            disp(x1);
            break
         end
         if k>N
            fprintf( '迭代次数超限\n' )
            break
         end
         x0=x1;
end
end

主函数：
A=[2 1 -5 1;1 -3 0 1;2 0 -1 2;1 4 -7 3];
b=[-1;4;3;4];
GS_iteration(A,b)

实验结果

（1）Gauss消去法：

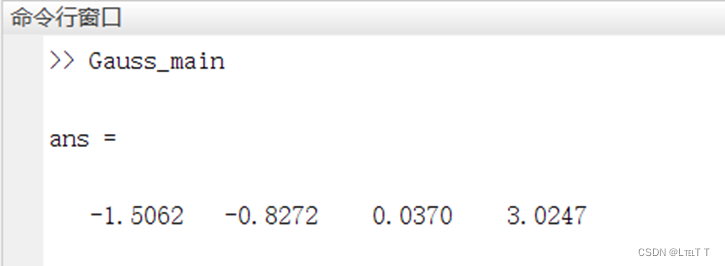
（2）LU分解法：

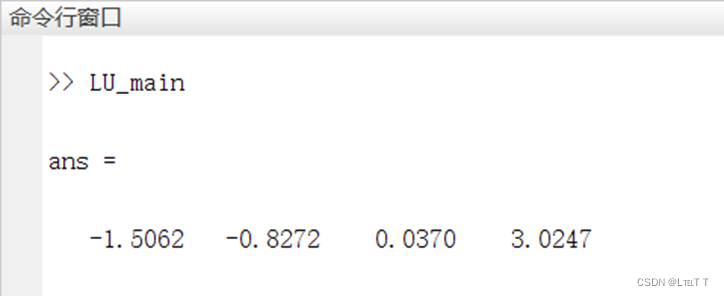
（3）Jacobi迭代法：


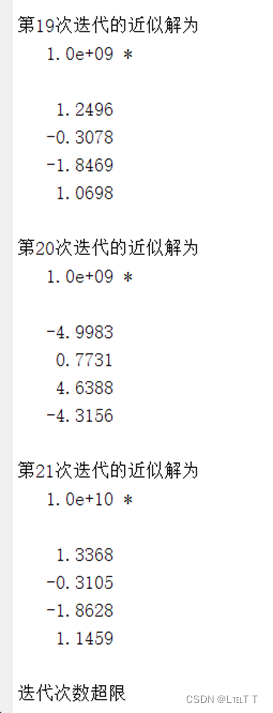
（4）Gauss-Seidel迭代法：

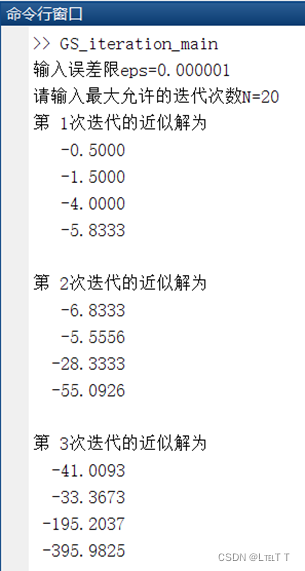
M文件以及程序文本

**已经全部打包压缩，包括一下所有的方法和代码实现
1、方程求根的数值方法 ：二分法、牛顿法、斜截法
2、求解线性方程组的数值方法：Gauss消去法、LU分解法、Jacobi迭代法、Gauss-Seidel迭代法
3、插值与数值积分：牛顿插值多项式、插值多项式p4(x)的图形并描点、复化梯形公式、复化Simpson公式
4、函数逼近和微分方程求解：最小二乘法、Euler法、改进的Euler法、四阶R-K法
**