第九届数维杯大学生数学建模挑战赛B题

杨先森只爱吃肉

已于 2025-03-10 14:40:27 修改

阅读量995

点赞数 24

文章标签：数学建模

于 2025-02-24 13:41:59 首次发布

本文链接：https://blog.csdn.net/weixin_48797293/article/details/145822449

版权

在这里给出24年的第九届数学建模竞赛以及相关题目部分解题思路

首先，附上B题的内容

2024年第九届数维杯数学建模B题完整分析参考论文（共42页）（含模型和代码）_数维杯2024b题第三问matlab代码-CSDN博客

通过分析题目可知，题目希望通过建立数学模型，使这个过程产生的能源和其他产物能够被更有效地利用。具体来说，研究关注了几个重要方面：首先，研究人员想要了解一种叫做"正己烷不溶物"(INS)的物质是如何影响热解过程的。这个物质与生物质和煤炭的混合比例之间可能存在某种相互作用，研究人员希望弄清楚这种关系。其次，研究团队致力于找出生物质和煤炭混合时的最佳配比。为了确保研究结果的可靠性，他们还比较了实验中实际得到的数据和理论计算预测的结果之间的差异。最终，他们希望建立一个可以准确预测热解产物产量的模型。因此，研究涉及: 1.分析INS对热解产率的影响; 2.探究 INS 与混合比例的交互效应; 3.优化共热解混合比例; 4.评估实验值与理论计算值之间的误差; 5.预测热解产物产率.

针对以上五个问题，我们分别给出以下解决方案：1. 采用皮尔逊和斯皮尔曼相关系数分析方法，确定了 INS 与热解产率的相关性；2. 通过双因素方差分析，我们探究了 INS 和混合比例的交互效应应；3. 构建了基于函数拟合的最优产出计算模型；4. 使用误差 t 检验模型评估实验值与理论计算值的误差；5. 建立了神经网络预测模型来预测热解产物产率。在这里我们主要展示问题1和5的模型建立和解决方法。

针对问题一，我们采用相关系数分析模型加以探讨，这一分析方法是用来研究两个及以上变量之间存在线性和非线性关系方法。这里使用皮尔逊系数(用于测量两个连续变量之间的线性相关程度)和斯皮尔曼系数(用于分析两个存在非线性或不满足正态分布的变量之间的相关性)，其中建模步骤为: 1.计算INS与焦油产率、水产率、焦渣产率的皮尔逊和斯皮尔曼系数；2.通过相关系数来判断是否显著相关(在这里我们设置相关系数为0.05)；3.通过热力图可视化这一结果

# %%
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 修改字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# %% 
data1 = pd.read_excel('./统计数据.xlsx')
data1.head()

# %%
# 数据预处理
# 去除第一行
data1 = data1.drop(0)
# 去除最后一列
data1 = data1.drop(data1.columns[-1], axis=1)
# 
for i in range(3):
    data1.iloc[:, i] = data1.iloc[:, i].fillna(method='ffill')
# 对于第6和10列，使用0补齐缺失值
data1.iloc[:, 6] = data1.iloc[:, 6].fillna(0)
data1.iloc[:, 10] = data1.iloc[:, 10].fillna(0)
data1.head()

# %%
# 分析皮尔逊相关系数
data_q1 = data1.iloc[:, [6, 7, 8, 9]]
from scipy.stats import pearsonr, spearmanr
corrs_pearson = []
ps_pearson = []
for i in range(1, 4):
    corr, p = pearsonr(data_q1.iloc[:, 0], data_q1.iloc[:, i])
    corrs_pearson.append(corr)
    ps_pearson.append(p)

# %%
# 分析斯皮尔曼相关系数
corrs_spearman = []
ps_spearman = []
for i in range(1, 4):
    corr, p = spearmanr(data_q1.iloc[:, 0], data_q1.iloc[:, i])
    corrs_spearman.append(corr)
    ps_spearman.append(p)


# %%
# 使用热力图进行绘制
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
# 皮尔逊相关系数热力图绘画
corrs_pearson = np.array(corrs_pearson)
ps_pearson = np.array(ps_pearson)
corrs_pearson[ps_pearson > 0.05] = 0
corrs_pearson = corrs_pearson.reshape(1, -1)
ax[0].imshow(corrs_pearson, cmap='coolwarm', vmin=-1, vmax=1)
ax[0].set_xticks(np.arange(3))
ax[0].set_yticks([0])
ax[0].set_xticklabels(data_q1.columns[1:])
ax[0].set_yticklabels(['INS'])
ax[0].set_title('皮尔逊相关系数')
# 在图像上标注相关系数和p值
for i in range(3):
    for j in range(1):
        ax[0].text(i, j, f'corr={corrs_pearson[j, i]:.2f}\np={ps_pearson[i]:.2f}', ha='center', va='center', color='black')
# 斯皮尔曼相关系数热力图绘画
corrs_spearman = np.array(corrs_spearman)
ps_spearman = np.array(ps_spearman)
corrs_spearman[ps_spearman > 0.05] = 0
corrs_spearman = corrs_spearman.reshape(1, -1)
ax[1].imshow(corrs_spearman, cmap='coolwarm', vmin=-1, vmax=1)
ax[1].set_xticks(np.arange(3))
ax[1].set_yticks([0])
ax[1].set_xticklabels(data_q1.columns[1:])
ax[1].set_yticklabels(['INS'])
ax[1].set_title('斯皮尔曼相关系数')
# 在图像上标注相关系数和p值
for i in range(3):
    for j in range(1):
        ax[1].text(i, j, f'corr={corrs_spearman[j, i]:.2f}\np={ps_spearman[i]:.2f}', ha='center', va='center', color='black')
# 显示色条
plt.colorbar(ax[0].imshow(corrs_pearson, cmap='coolwarm', vmin=-1, vmax=1), ax=ax[0], orientation='horizontal')
plt.colorbar(ax[1].imshow(corrs_spearman, cmap='coolwarm', vmin=-1, vmax=1), ax=ax[1], orientation='horizontal')
plt.show()

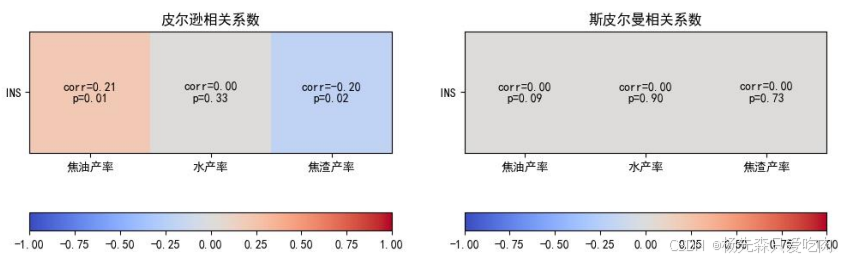
我们利用 scipy.stats.pearsonr 和 scipy.stats.spearmanr 函数分别进行皮尔逊和斯皮尔曼系数的分析。皮尔逊的相关系数分析，可知INS与焦油产率、水产率、焦渣产率的相关系数值分别为0.01、0.33、-0.2，分别小于、大于以及与设定值相反，说明INS只和焦油产率相关；斯皮尔曼的相关系数分析，可知INS与焦油产率、水产率、焦渣产率的相关系数值均大于设定值0.05，因此也并不相关。

针对问题五，我们利用神经网络模型来实现高精度的预测，预测热解过程中焦油、水和焦渣的产率。总共分为以下几个过程:数据输入-数据输出-神经模型搭建-训练神经模型-测试与评估。下面简单展示我通过sklearn进行神经网络预测产率的相关代码：

# %%
# 使用神经网络进行预测预测热解过程中焦油、水和焦渣的产率
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
# 数据预处理
data1 = data1.dropna()
X = data1.iloc[:, [3, 4, 5, 6, 11]]
y = data1.iloc[:, 7:10]
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 训练模型
model = MLPRegressor(hidden_layer_sizes=(100, 100), max_iter=1000, random_state=0)
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 计算均方误差
mean_squared_error(y_test, y_pred)

# %%
# 绘图查看训练集和测试集的预测效果
fig, ax = plt.subplots(3, 2, figsize=(12, 18))
for i in range(3):
    for j in range(2):
        if j == 0:
            ax[i, j].plot(range(y_train.shape[0]), y_train.iloc[:, i], label='实际值')
            ax[i, j].plot(range(y_train.shape[0]), model.predict(X_train)[:, i], label='预测值')
            ax[i, j].set_title('训练集 ' + y_train.columns[i])
            ax[i, j].legend()
        else:
            ax[i, j].plot(range(y_test.shape[0]), y_test.iloc[:, i], label='实际值')
            ax[i, j].plot(range(y_test.shape[0]), y_pred[:, i], label='预测值')
            ax[i, j].set_title('测试集 ' + y_test.columns[i])
            ax[i, j].legend()
plt.show()

如下所示，以焦油产率为例展示我们的训练结果和预测结果：