首先定量的衡量两个模型之间的差异有这些:1、最小二乘法,2、极大似然估计法,3、交叉熵
交叉熵主要使用了熵这个概念,将模型转换成熵这么一个数值,然后再使用这个数值去比较不同的模型之间的差异信息。为什么需要使用熵去绕这么一圈,首先要知道,比较两个模型之间的障碍有哪些,如果两个模型属于同一种类型的模型,那么只需要比较两个模型之间的参数就行了,例如都是高斯分布的话,只需要比较他们的方差和期望即可;如果两个模型属于不同的类型,例如一个属于高斯分布,另一个则属于正态分布,那么就无法直接比较了。
而熵则是将不同类型之间的模型得以用同一个标准来衡量。熵在通俗意义上来讲的话,它表示的是一个系统的混乱程度,神经网络里面也是一个概率模型,这也就说明他们也是有一定的混乱程度的,那么是否可以使用熵去衡量呢,这就需要深入的挖掘熵的根本的含义。
熵这个词即是热力学上的概念也是信息论的概念,在深度学习上来讲的话,我们就需要从信息论的基础之上去了解一下熵的真正含义。
要想弄明白熵这个概念,首先我们需要知道信息量这个前置概念。
信息量
信息量,对于这个词来说,在平时口语交流中就会用到,比如说你读了一本书,觉得里面讲的不好,就会说:这本书里面一点信息量都没有,内容真差。再比如说一个新闻说比尔.盖茨中午吃了个汉堡,并且没吃薯条。这个东西确实是你不知道的,但是却貌似也没有什么信息量。所以这样来说的话,看一个信息有没有信息量,不仅仅是看这个信息是否为我们所知,还要就看这个信息能够为我们带来多少的确定性。
下面再举一个例子来说明信息量:
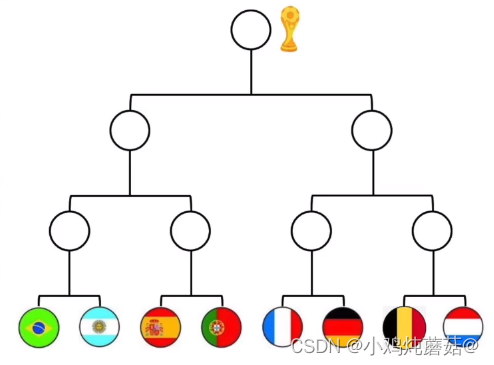
假设有这样的8支球队,每个球队夺冠的概率是相同的,那么球队A夺冠的概率就是1/8,这是不确定的,但是有一天有人说球队A夺冠了,那么这就从一个不确定的事件变成了一个确定的事件,那么这样的话这个信息量就是很高的了,但是如果这个事件变成球队A进入了决赛,这也是有信息量的,因为表示球队A夺冠的概率从1/8变为了1/2,相对与球队A夺冠这个事件来说,我们很容易就能知道肯定是球队A夺冠这个事件所含的信息量更高,因为一个夺冠的概率是1,表示确定性的事件,而另一个夺冠的概率只是1/2,它依然包含不确定性。
通过以上例子可以明白,不同的信息包含的信息量肯定是不一样的,那么如何将这里面的不一样进行量化,如何计算就成为了我们需要思考的问题。
看这个式子:

假设是计算信息量的一个方程,目前的任务就是要去尝试寻找他的这样一个表达式。特别注意一下 “ := ” 这样一个符号表示用后面的东来去定义前面的东西(与 “ = ” 还是有一些区别的)。我们希望给出信息量定量的定义,就希望我们给出的的定义可以在它自身的体系下自洽,而关于如何自洽的问题,我们看回到上面所举出的球队的例子,按照对信息量的理解可以得到以下的式子:
f(球队A夺冠) = f(球队A进入决赛) + f(球队A赢了决赛)
这个式子表示球队A夺冠的信息量和球队A进入决赛加上球队A赢了决赛信息量加在一起是一样的,原因如下图所示:
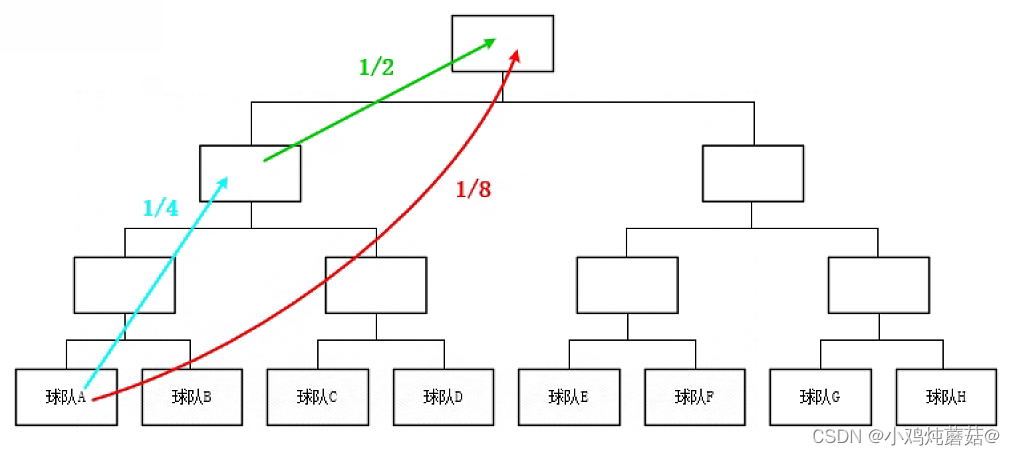
第一种方式是直接告诉一个信息球队A夺冠了,那么球队A夺冠的不确定性就从原来的1/8提升到了1。
那么换种方式,没有直接告诉球队A夺冠了,而是先告诉球队A进入决赛,然后再告诉球队A赢了决赛,这样也能说明球队A夺冠了,球队A夺冠的不确定性也从原来的1/8提升到了1。
所以说这两种方式,虽然两者说明的方式不同,但两种方式携带的信息量是一样的,从图中我们还可以看出上述公式中的自变量是什么,即路径的长短(夺冠的概率值),那么前面提到的式子可以写成如下形式:
到了这一步,f函数的可以有无数种可能性使其自身自洽,回到夺冠的事件上来,这里它本身是一个概率,那么还可以有以下式子:
P(球队A夺冠)=P(球队A进入决赛)+P(球队A赢了决赛)
这个式子表示球队A夺冠必须要球队A进入决赛和球队A赢了决赛这两件事情同时发生才行,而两件事情同时发生的概率即将两件事情分别发生概率的乘积。所以说f函数必须要同时满足以上两个式子才能使得整个系统自洽,具体来说可以表述成以下形式:
也就是说 f 函数最终需要满足这个式子才行,那么如何才能使得自变量相乘移出来之后变成两个函数值相加呢?所以为了保持自洽,那么最终的式子中必须带有 log 才行,现在还有系数和以什么数为底没有确定。
先说系数,最简单的是使用1即可,但是这并不符合我们的要求,我们希望一件事情发生了,它之前的概率(x)越小,代表的信息量越多,所以我们希望将原本单调递增的 log 函数转换方向,变为单调递减,在前面加上一个负号即可,到此为止已经可以不用再探索 log 函数以哪个数字为底就已经可以保持自洽了,这里我们先将底设为2,这样可以计算出上面的式子的值:
表示球队A夺冠的概率为1/8到最终夺冠,这件事情的信息量是3, 如果是以2为底的话,那这样其实就类似于使用抛硬币来衡量信息量,这是怎么回事呢?举例来说,如果一件事情发生的概率是1/2,那么就等价于抛1枚硬币正面朝上的概率,如果一件事情发生的概率是1/4,那么就等价于抛2枚硬币全部正面朝上的概率,但是如果是1/3呢,那么这就表示发生的概率介于抛1枚硬币和2枚硬币全部正面朝上的概率之间,但是现实生活中却又不可能出现半枚硬币的情况,数学上我们依然可以理解为抛了1.5个硬币全部正面朝上的概率。
并且以2为底计算出来的信息量的单位称为比特。依然使用球队的例子,例如球队B的水平比较低,夺冠的概率只有1/1024,假如说你告诉我球队B夺冠了,那么根据以上的内容可以知道这里面包含的信息量是很高的,计算出来它的信息量应该有10比特。
总结下来,信息量可以理解为一件事情从不确定变成确定后它的难过有多大。信息量大表示难度越大。
熵
熵也类似,只是熵并不是衡量某一个具体的事件,而是衡量整个系统里面的所有事件,也就是说一个系统从不确定变成确定后它的难过有多大。两者都是衡量难度大小,所以单位也可以一样,都是比特。举一个简单的例子,如下图所示
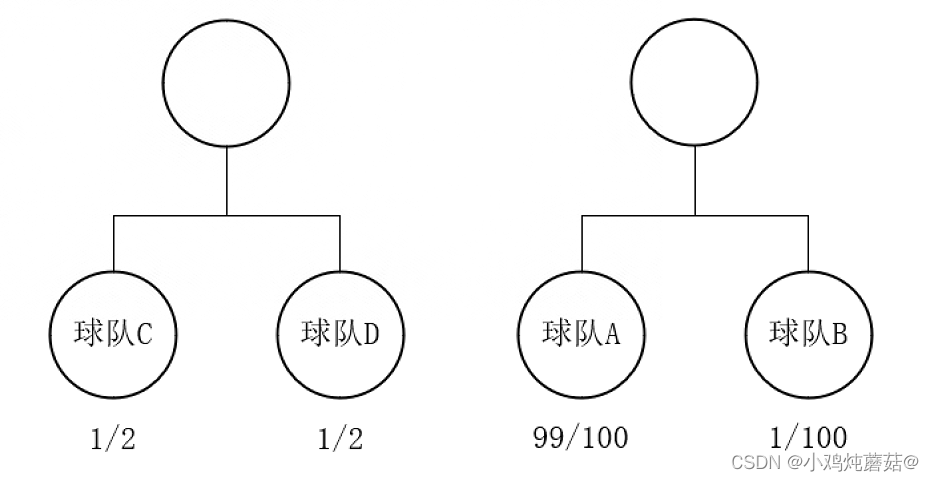
有两场比赛,第一场比赛球队C对阵球队D,两支球队实力相近,胜利的概率都是1/2;第二场比赛是球队A对阵球队B,这里球队A的实力远强于球队B,两支球队胜利的概率分别是99/100和1/100。可以利用上述公式计算出他们的信息量并计算出对整个系统的信息量,如下图所示:
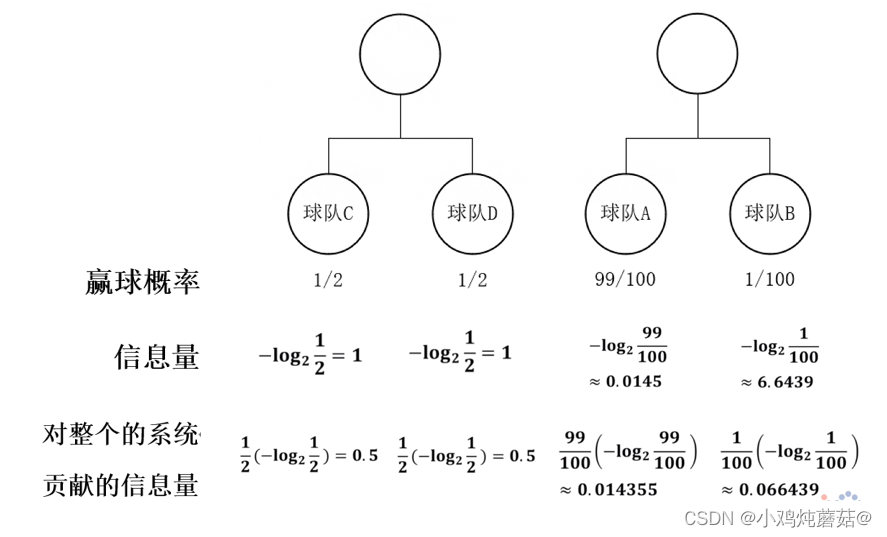
对上图的解释我们可以认为计算出单个事件的信息量后,还需要乘上发生的概率才能得到对整个系统贡献的信息量,最终将所有事件对系统贡献的信息量相加就可以得到最后我们所要求的熵。回顾整个过程,将每个事件的值乘上对应的概率,这不就是求期望的公式吗,所以说到这里我们就可以对熵进行定义了。
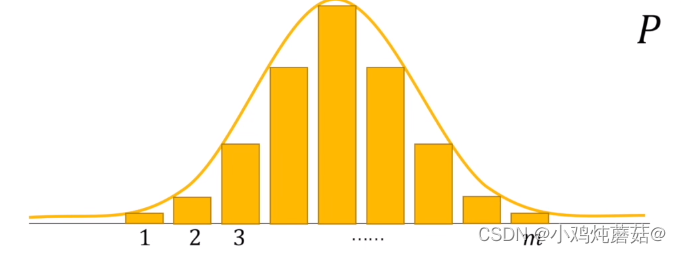
假如说有一个概率系统P,分布图如上图所示,我们对其熵进行定义,定义成对这个系统求期望,定义公式如下:
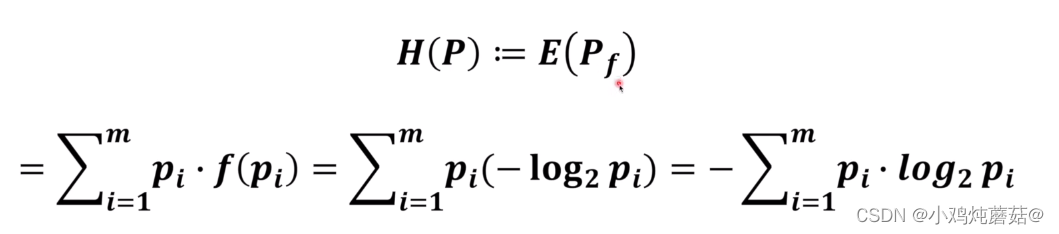
其中,也就是信息量的期望,接着将其展开再计算就可以得到最终的形式,所以说熵的求解就是将一个系统中所有事件的信息量求出来,再与对应的概率相乘后累加,最终得到的就是这个系统的熵。
通过对熵的定义我们可以知道熵其实是对系统的整体的概率模型进行的一个衡量,衡量的结果则反映出整个系统的不确定程度或者说是混乱程度。
相对熵
再次回到初始的问题:比较两个模型。到这里我们可以知道最简单的方法就是将两个模型的熵计算出来进行比较,当然这样会存在一个问题,若其中有一个模型不知道的话就无法计算其对应的熵,也就无法比较了,所以引入了一个新的概念:相对熵,也叫KL散度。
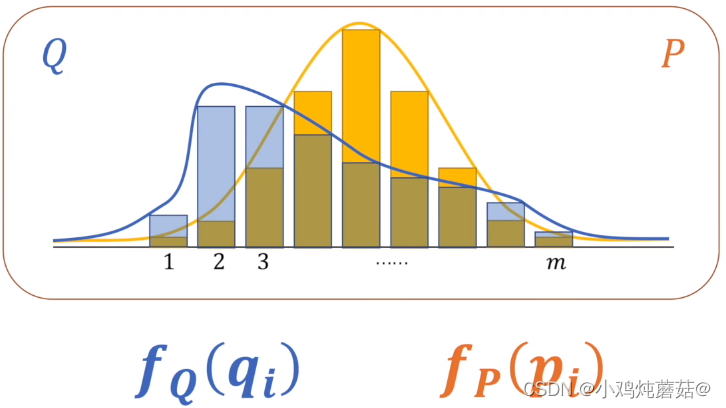
如上图所展示的,存在两个概率系统 Q和P, 上面是两个系统的概率分布图。两个系统的信息两分别使用和
表示,下面,我们来看KL散度的定义公式:
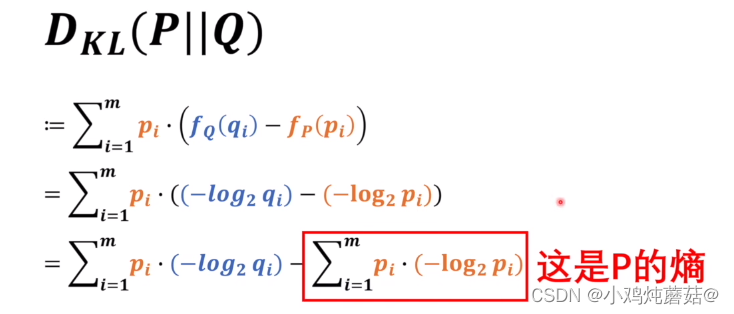
这里我们是将P作为基准,去考虑Q和P相差有多少,从式子中可以看到我们将系统中Q的信息量减去P的信息量得到差值,最后再求P的整体的期望。这里如果P和Q相等的话,可以看到最终的结果是等于0的,那么反过来如果不等于0的话是不是就说明P和Q是不相等的。上面的式子展开到最后,我们看到后面部分,是不是可以发现后面一部分其实就是P的熵,这里我们将P作为基准,所以他的熵是恒定的,所以说衡量P和Q之间的关系关键就在于看前面的这一部分,而这部分就是我们所要求的交叉熵了,使用 H(P, Q) 来表示的。

到这里,我们考虑到一个事件的熵一定是一个大于0的数,关键在于我们需要知道最终的式子是一个相减的过程,那么最终结果到底是正的还是负的呢?这里吉布斯不等式已经证明了,如下:

所以到这里我们可以确定最终KL散度的值一定是大于等于0的,我们希望Q的概率模型越接近于P的概率模型就是希望他们的交叉熵的值越小。换句话说就是交叉熵越小代表着两个概率模型越相近。
神经网络中交叉熵的应用
首先给出计算公式:

先写出交叉熵的定义公式,将里面的参数换成神经网络中实际的参数,比如说一个识别图像中是否为猫的神经网络,其中n表示需要识别的图片数量,用替换掉概率模型
,表示图片中是猫的情况,那么是否可以直接用模型预测出来的值
替换原本的
呢?首先需要明白
表示的是模型将图片中预测为是猫的概率,我们的
需要和
对应起来的话,那么这个式子还需要继续展开,也就是说
对应的是
,即预测为是猫的概率(当图片中是猫的时候,
需要判断的是有多像猫的概率),
对应的是
,即预测为不是猫的概率( 当图片中不是猫的时候,
需要判断的是有多不像猫的概率)。看到最终我们展开的式子,可以发现这个式子跟吴恩达所讲的是一样的,也就是说这跟使用极大似然估计法推出来的式子是相同的。
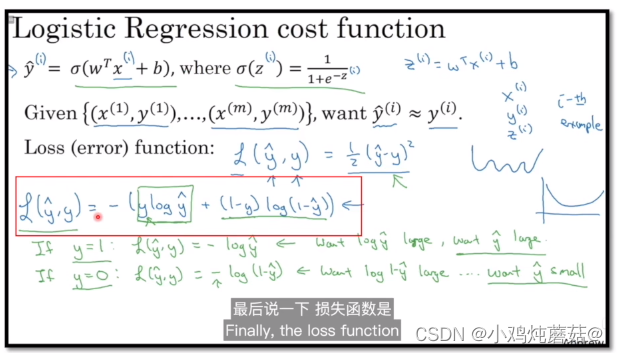
最后,这里可以看到使用交叉熵和使用极大似然估计法推出来的式子是一样的,当然这只是形式上的一样,比如说极大似然估计法中的log引入的原因是不同的。
参考文献





















 3688
3688











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








