无线系统（EEEN3006J-Wireless Systems）复习笔记 (2)

爱财如命的阳老板

已于 2022-05-05 18:34:17 修改

阅读量1k

点赞数 1

分类专栏： BDIC课程文章标签：学习

于 2022-05-05 16:30:02 首次发布

本文链接：https://blog.csdn.net/weixin_49109579/article/details/124510184

版权

BDIC课程专栏收录该内容

22 篇文章 38 订阅

订阅专栏

前言：

Chapter 2: Some preliminaries before we study Maxwell’s equations

1. 向量代数（Vector algebra）

1.1 点乘（Dot product）

1.2 叉积（Cross product）

1.3 三重积（Triple product）

1.4 坐标系（Co-ordinate systems）

2. 向量演算（Vector calculus）

2.1 梯度（Gradient）

2.2 散度（Divergence）

2.3 旋度（Crul）

2.4 乘法规则（Product rules）

3. 亥姆霍兹定理（Helmholtz theorem）

4. 电势（Potentials）

5. 积分学（Integral calculus）

5.1 直线积分（Integration over a line）

5.2 电荷和电流（Charge and current）

前言：

本笔记是基于北京都柏林学院2022年EEEN3006J-Wireless Systems课程课件总结出的笔记。任课教师为Dr. Declan Delaney.

•在这堂课中，我们将回顾一些用于电磁理论的数学。

•这将帮助你在接下来的几节课中理解麦克斯韦方程组。

•根据麦克斯韦方程，我们将最终描述天线的工作原理。

Chapter 2: Some preliminaries before we study Maxwell’s equations

1. 向量代数（Vector algebra）

1.1 点乘（Dot product）

两个向量A和B的点积（或标量积或内积）由下式给出：

$A\cdot B=\sum^n_{i=1}A_iB_i=A_1B_1+A_2B_2+A_3B_3+\cdots +A_nB_n$

或

$A\cdot B=\left \| A \right \|\left \| B \right \|cos\theta$

1.2 叉积（Cross product）

可以使用右手法则获得点积的方向。

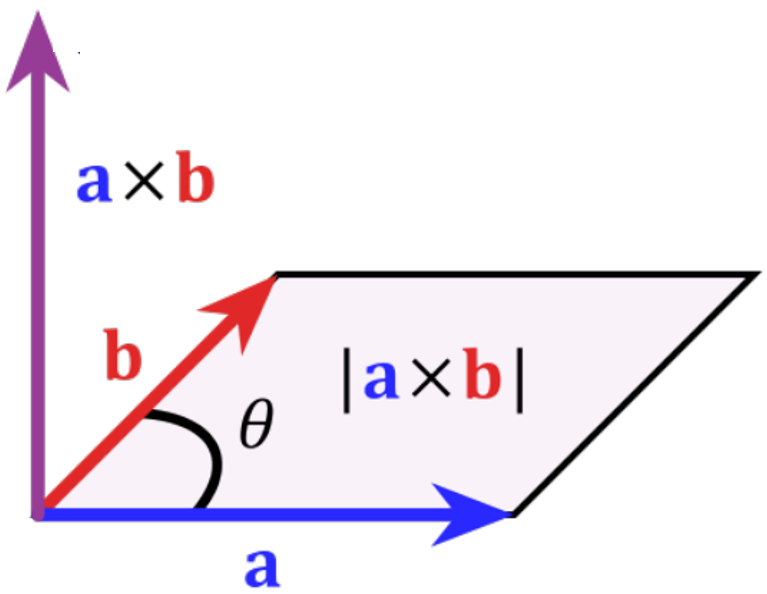
叉乘公式如下：

$a\times b = \left \| a \right \|\left \| b \right \|sin\theta \cdot n$

叉积计算平行四边形的面积，如图所示:

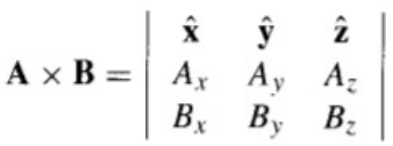
1.3 三重积（Triple product）

三重积公式如下：

$a\cdot (b\times c)=b\cdot (a\times c)= c\cdot (a\times b)$

三重积计算平行六面体的体积，如图所示：

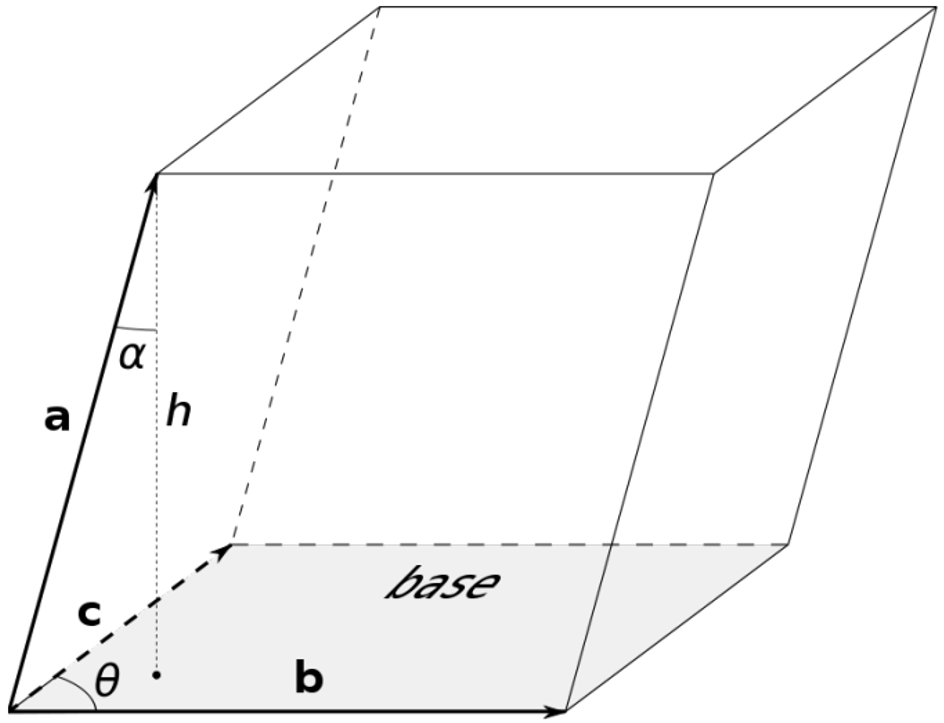
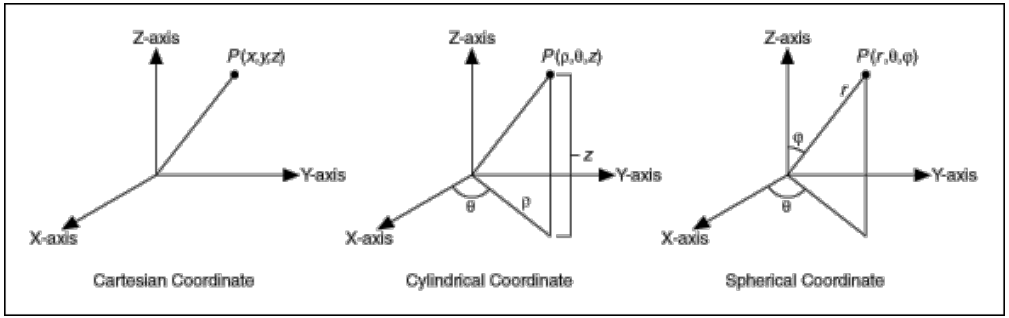
1.4 坐标系（Co-ordinate systems）

•大多数人比较熟悉笛卡尔坐标。

•在本课程中，有时需要切换到球面极坐标或圆柱坐标以解决问题。

2. 向量演算（Vector calculus）

在处理电磁学时，我们更喜欢使用向量演算。

有三项重要的操作：

•梯度 •散度 •旋度

2.1 梯度（Gradient）

•适用于标量字段：

•呈现出每个点的坡度方向和陡度。

练习：

村庄附近以m为单位的山的高度由函数描述：

$h(x,y)=10(2xy-3x^2-4y^2-18x+28y+12)$

x是村庄以东的距离，单位为km，y是村庄以北的距离。

问：

a）找到山顶。

b）这座山有多高？

c）我想在村子北边1公里和东边1公里处建一栋房子。这里的山有多陡？

d）此时，斜坡的走向是什么？

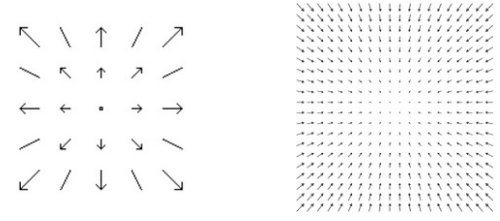
2.2 散度（Divergence）

•在物理学的许多领域都很重要。

•稍后我们将讨论电通量。通量和散度都处理场的流动，但通量是在一个区域上定义的，而散度处理点。

散度公式为：

标量：没有方向。

–正散度图像为发撒

–负散度图像为汇聚

球坐标公式（Spherical co-ordinates）：

$\overrightarrow{ \triangledown }\circ \overrightarrow{A} = ( \frac{1}{r^2}\frac{\partial }{\partial r}(r^2A_r)+ \frac{1}{rsin\theta }\frac{\partial }{\partial \theta}(A_\theta sin\theta)+ \frac{1}{rsin\theta }\frac{\partial A_\phi }{\partial \phi})$

柱坐标公式（Cylindrical co-ordinates:）：

$\overrightarrow{ \triangledown }\circ \overrightarrow{A} = ( \frac{1}{r}\frac{\partial }{\partial r}(rA_r)+ \frac{1}{r}\frac{\partial A_\phi }{\partial \phi}+\frac{\partial A_z }{\partial z})$

练习：

计算下列函数的散度：

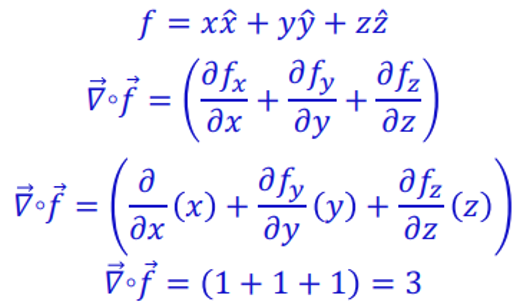
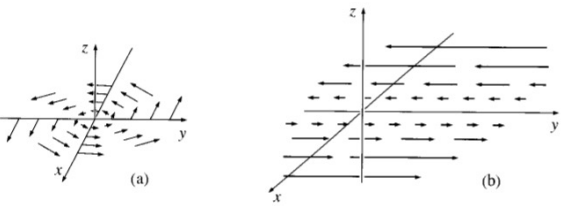
2.3 旋度（Crul）

可以被定义为：

$\overrightarrow{\triangledown }\times \overrightarrow{A}=\begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\ A_x&A_y & A_z \end{vmatrix} \\= (\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z})\overrightarrow{i} +(\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x})\overrightarrow{j}+(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y})\overrightarrow{k}$

旋度的每个分量表示磁场在一个坐标平面内旋转的趋势。

练习：

计算旋度：

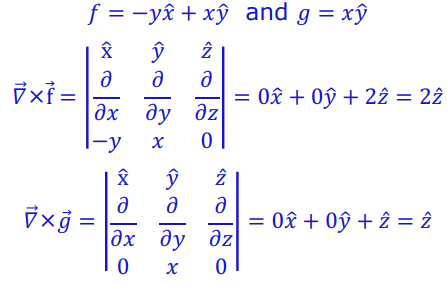
2.4 乘法规则（Product rules）

•梯度的旋度（Curl of Gradient）始终为零：

拉普拉斯算子（即梯度的散度,Divergence of Gradient）

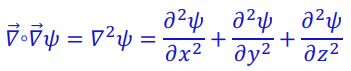
我们可以使用这些来获得泊松方程(Poisson's equition)。(后面的博客中我们会讲到。)ヾ(ｏ･ω･)ﾉ

散度的梯度(Gradient of Divergence)减去拉普拉斯算子(Laplacian)就是旋度的旋度(Crul of Crul)。

3. 亥姆霍兹定理（Helmholtz theorem）

如果我们知道一个域的散度(divergence)和旋度(crul)，你能唯一地定义这个域吗？

–不，我们还需要边界条件。

•亥姆霍兹定理告诉我们，如果我们要求场在无穷远处为零，我们可以唯一地定义给定旋度(divergence)和散度(crul)的场。

4. 电势（Potentials）

如果一个场的旋度为零（我们会遇到很多场），那么这个场可以写成标量势的梯度。

$\triangledown \times F = 0\Leftrightarrow F = -\triangledown V$

5. 积分学（Integral calculus）

•线积分、面积分和体积积分

•微积分基本定理

•梯度的基本定理

•发散的基本定理

•卷曲的基本定理

•部件集成

5.1 直线积分（Integration over a line）

移动电荷a到b所做的总功

$W = \int_{a}^{b} \overrightarrow{F} \cdot \overrightarrow{dl}$

a到b每单位长度（直线方向）力的积分

5.2 电荷和电流（Charge and current）

•电荷运动产生电流。

•电流单位为安培（A）

爱财如命的阳老板

关注

1
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
无线系统（EEEN3006J-Wireless Systems）复习笔记 (2)

前言：本笔记是基于北京都柏林学院2022年EEEN3006J-Wireless Systems课程课件总结出的笔记。任课教师为Dr. Declan Delaney.
复制链接

扫一扫