【矢量分析】工科矢量分析注意事项与结论

---

公式大全

工科矢量分析公式大全

区分坐标系的坐标式与分量式

对于一个矢量 $\vec{A}=(x,y,z)$ ，可以写成 $\vec{A}=x\overrightarrow{e_1}+y\overrightarrow{e_2}+z\overrightarrow{e_3}$
其中 $\overrightarrow{e_1},\overrightarrow{e_2},\overrightarrow{e_3}$ 是相互正交的单位矢量，是这个空间的矢量的一组基

对于空间直角坐标系，其坐标表达式 $(x,y,z)$ 就是其在单位矢量上的分量式 $(A_x,A_y,A_z)$，
其中 $A_x=x,A_y=y,A_z=z$

对于柱坐标系，其坐标表达式 $(\rho ,\varphi ,z)$ 并不是其在单位矢量上的分量式 $(A_{\rho },A_{\varphi },A_z)$ ，
不能用坐标表达式进行点乘叉乘

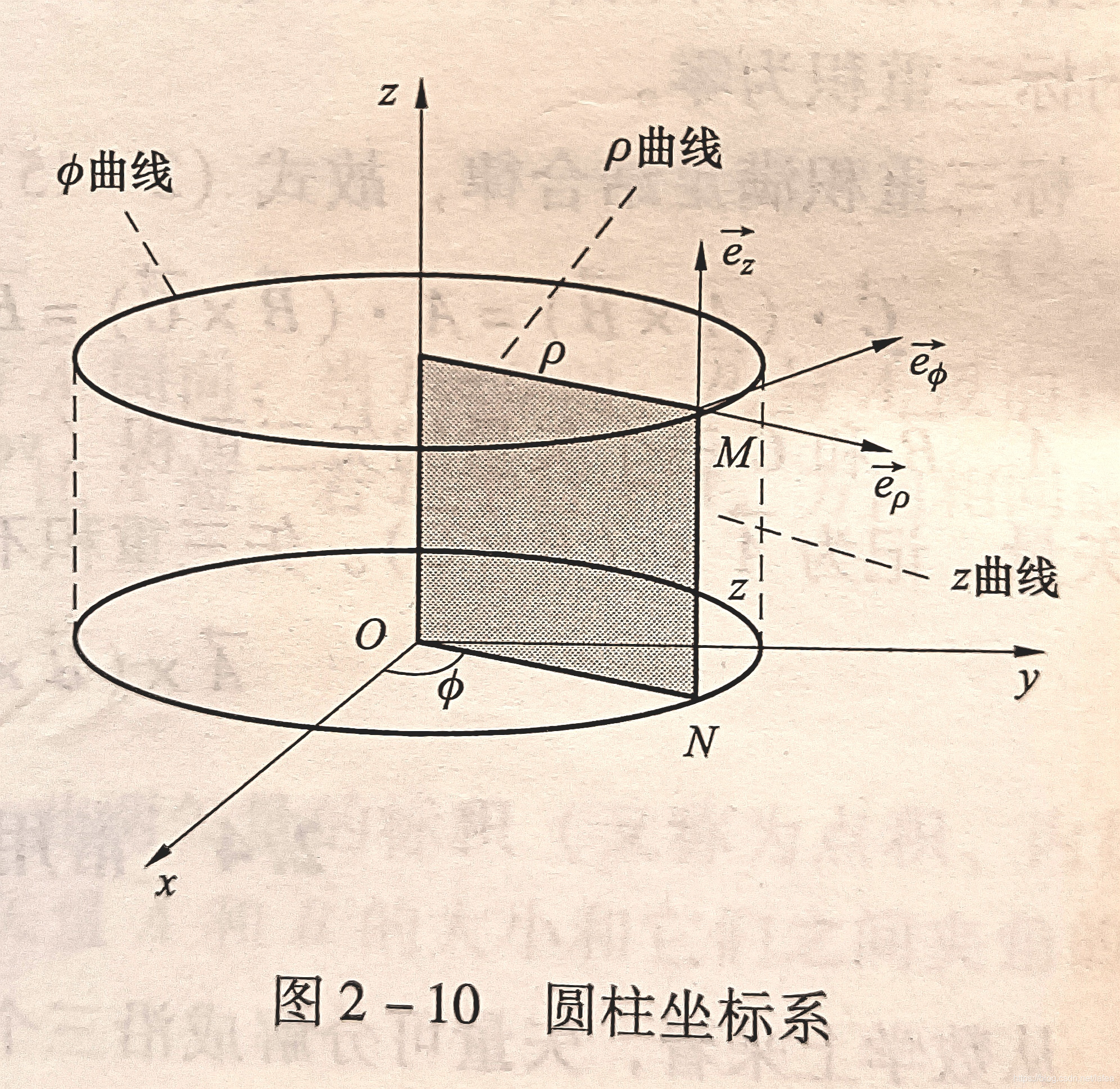
可以看到，柱坐标系的单位矢量仍然是正交的 $(\rho ,\varphi ,z)\ne (A_{\rho },A_{\varphi },A_z)$

对于求坐标系，其坐标表达式 $(r,\theta ,\varphi )$ 并不是其在单位矢量上的分量式 $(A_r,A_{\theta },A_{\varphi })$ ，
不能用坐标表达式进行点乘叉乘

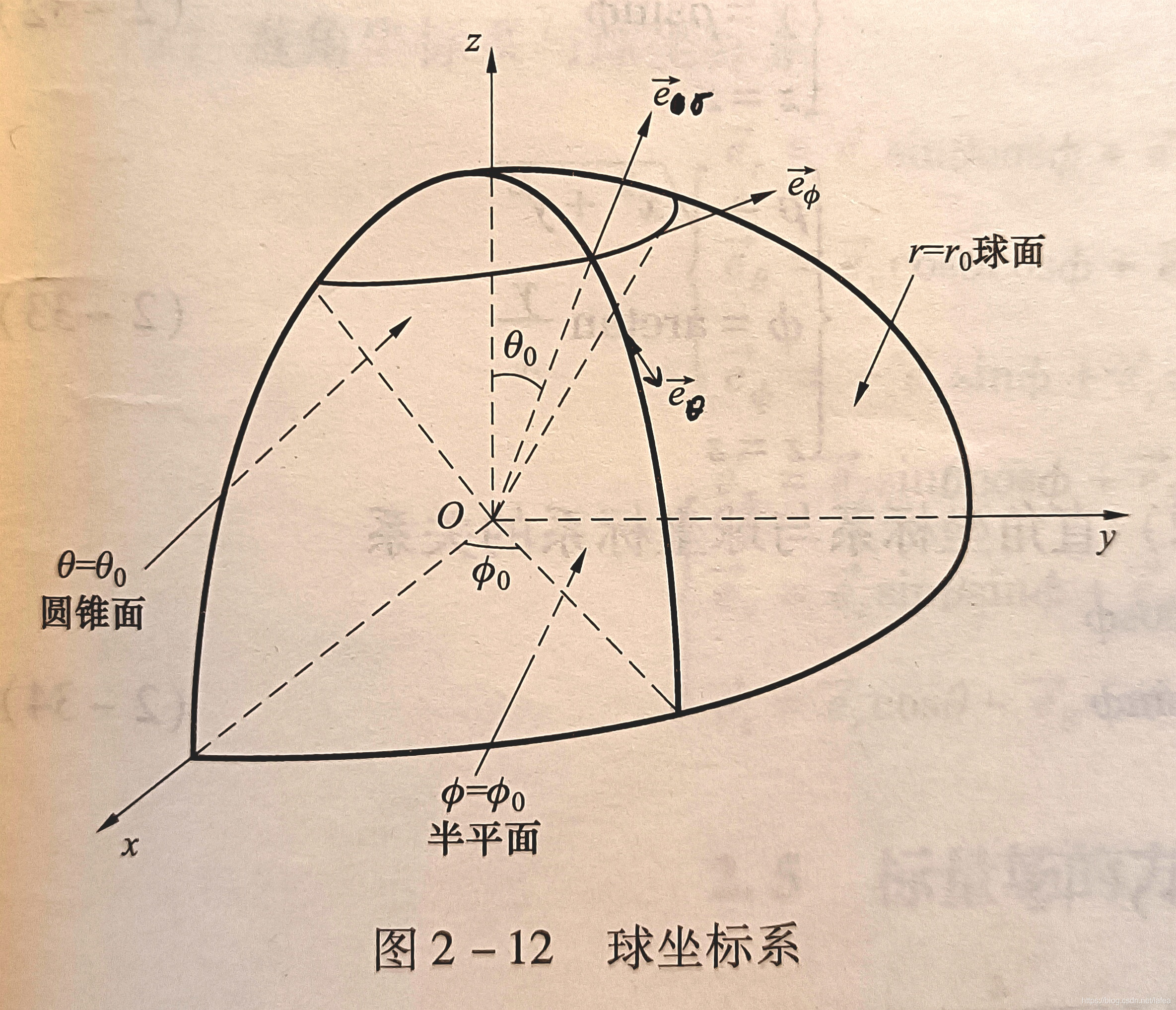
可以看到，球坐标系的单位矢量仍然是正交的 $(r,\theta ,\varphi )\ne (A_r,A_{\theta },A_{\varphi })$

单位径矢的公式

$$\begin{gathered} 直角坐标系：\overrightarrow{e_r}=(\frac{x}{r},\frac{y}{r},\frac{z}{r}) \\ 柱坐标系：\overrightarrow{e_r}=(\frac{\rho }{r},0,\frac{z}{r}) \\ 球坐标系：\overrightarrow{e_r}=(1,0,0) \\ 通过三系转换计算，注意以上都是分量式而不是坐标 \end{gathered}$$

区分场与势的概念

势和场是两个概念，通过矢量场可以定义出场的势
当0势能面确定后，可以定义出势能场（标量场）

对保守（无旋）的矢量场，可以定义出其势能场

径矢的公式

$$\begin{gathered} \nabla \cdot (\vec{a}\times \vec{r})=0 \\ \nabla \cdot (\vec{r}\times \vec{A}(r))=0 \\ \nabla (\frac{1}{r})=-\frac{\vec{r}}{r^3} \end{gathered}$$

一些屁话

无旋即保守，无散即无源