高等数学（第三章：一元积分学 ② ）

Kusunoki_D

已于 2025-04-26 20:09:50 修改

阅读量1.1k

点赞数 19

分类专栏：考研数学文章标签：高等数学积分考研

于 2024-10-18 23:35:52 首次发布

本文链接：https://blog.csdn.net/weixin_49272453/article/details/142904336

版权

考研数学专栏收录该内容

15 篇文章

订阅专栏

一、积分的概念总结

【思考】：

什么情况下原函数存在？
原函数存在定理。
什么情况下可积？
可积的充分条件。
原函数存在与可积有什么关系？
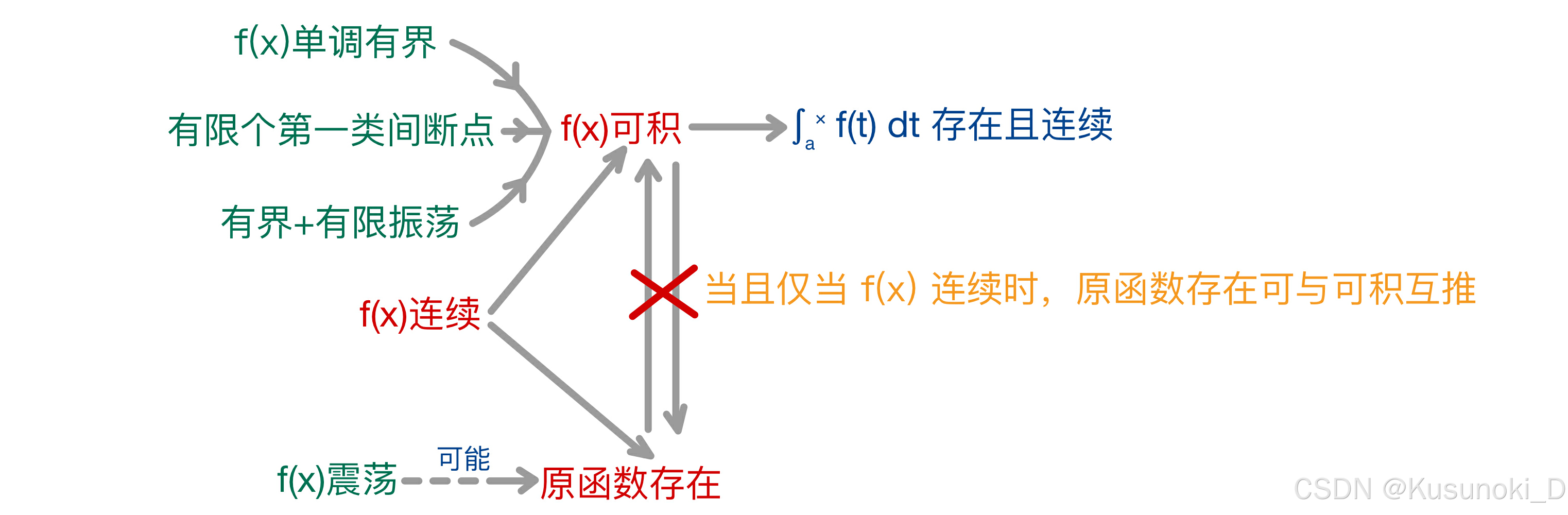
原函数存在不一定可积，可积不一定原函数存在（当且仅当 f(x) 连续时，原函数存在与可积可以互推）。
∫₀^x f(t) dt 一定是 f(x) 的一个原函数吗？
不是，原函数一定可导，但是 ∫₀^x f(t) dt 不一定可导（若 f(x) 有有限个跳跃间断点，则其变上限积分不可导）。
(∫₀^x f(t) dt)’ = f(x) 吗？
不是，若 f(x) 有有限个跳跃间断点，那么它可积（∫₀^x f(t) dt 存在），但是其变上限积分不可导（(∫₀^x f(t) dt)’ 不存在）。

【注】：若 f(x) 存在原函数，则称 F(x) = ∫₀^x f(t) dt 为 f(x) 的原函数；
若 f(x) 不存在原函数但可积，则称 F(x) = ∫₀^x f(t) dt 为 f(x) 的变上限积分。

1. 原函数存在与可积

1）原函数存在（不定积分）

① 定义：设 f(x) 在某区间 I 上，若存在可导函数 F(x) ，对于该区间上任意一点，都有 F’(x) = f(x) 成立，则称 F(x) 是 f(x) 在区间 I 上的一个原函数。（原函数一定要可导）

【注】：

若 f(x) 连续，那么 F(x) = ∫₀^x f(t) dt 为 f(x) 的一个原函数。
若 f(x) 连续，那么 ∫ f(x) dx = ∫₀^x f(t) dt + C 。

② 原函数存在定理：

f(x) 连续 ⇒ 原函数存在。
设 f(x) 在区间 I 上连续，则 f(x) 在区间 I 上存在原函数。
f(x) 可去、跳跃、无穷 ⇒ 原函数不存在。
若 f(x) 在区间 I 上有第一类间断点（可去、跳跃）和无穷间断点，则 f(x) 在区间 I 上没有原函数。
f(x) 振荡 ⇒ 原函数可能存在。
若 f(x) 在区间 I 上有振荡间断点，在区间 I 上可能有原函数。

③ 不定积分的基本性质：

∫ dF’(x) = F’(x) + C
d[∫ f(x) dx] = f(x) dx

2）可积（定积分）

① 可积的充分条件（条件推结论）

连续可积。
设 f(x) 在 [a, b] 上连续，则 f(x) 可积，∫_a^b f(x) dx 存在。
单调有界可积。
设 f(x) 在 [a, b] 上单调有界，则 f(x) 可积，∫_a^b f(x) dx 存在。
有限个第一类间断点（可去、跳跃）可积。
设 f(x) 在 [a, b] 上只有有限个第一类间断点，则 f(x) 可积，∫_a^b f(x) dx 存在。
有界（排除无穷）+ 有限个间断点（可去、跳跃、振荡）可积。
设 f(x) 在 [a, b] 上有界，且只有有限个间断点，则 f(x) 可积，∫_a^b f(x) dx 存在。

② 可积的必要条件（结论推条件）

若 f(x) 在 [a, b] 上可积，则 f(x) 在 [a, b] 上有界。
若 f(x) 在 [a, b] 上无界，则 f(x) 在 [a, b] 上不可积。（逆否命题）

3）总结

	连续	可去	跳跃	无穷	振荡
原函数存在	√	×	×	×	可能
定积分存在	√	有限	有限	×	有界+有限
变限积分可导性	可导	可导（极限）	不可导	/	/

判断函数是否存在原函数、是否可积的步骤：

第一步：判断函数是否连续，若连续则一定存在原函数、一定可积。
第二步：若不连续，则判断间断点（可去、跳跃、振荡、无穷）的类型和个数。
【可去、跳跃、无穷间断点必不存在原函数，振荡间断点可能存在原函数，需要进一步利用极限来判断。】
第三步：判断函数是否有界。
【无穷间断点（无界）必不可积，若可去、跳跃间断点的个数有限则可积，若振荡间断点的个数有限且函数有界则可积。】

【注】：

f(x) 在区间内连续，既可推原函数存在，又可推可积。
可积不一定原函数存在，原函数存在不一定可积。
f(x) 在区间内连续是原函数存在与可积之间的 “桥梁” 。

2. 变上限积分

1）定理

若 f(x) 在 [a, b] 上连续，则变上限积分 ∫₀^x f(t) dt 在 [a, b] 上可导，且 (∫₀^x f(t) dt)’ = f(x) 。

2）连续性

若 f(x) 在 [a, b] 上可积（变上限积分存在），则变上限积分 ∫₀^x f(t) dt 在 [a, b] 上连续。

3）可导性

若 f(x) 在 [a, b] 上除点 x = x₀ 外均连续，则在点 x = x₀ 处变上限积分 ∫₀^x f(t) dt 可导。

【注】：

可积有变上限积分，但该变上限积分未必是原函数。
f(x) 可积 → ∫₀^x f(t) dt 连续；f(x) 连续 → ∫₀^x f(t) dt 可导。（可导 → 连续 → 可积）
f(x) 可去 → ∫₀^x f(t) dt 可导；f(x) 跳跃 → ∫₀^x f(t) dt 不可导。

3. 奇偶性、周期性

关注 ∫₀^x f(t) dt — f(x) — f’(x) 的关系。

1）f(x) 可导（f(x) → f’(x) ，f’(x) 连续）

若 f(x) 是可导的奇函数，则 f’(x) 是偶函数。
若 f(x) 是可导的偶函数，则 f’(x) 是奇函数。
若 f(x) 是可导的周期为 T 的周期函数，则 f’(x) 是周期为 T 的周期函数。

2）f(x) 可积（f(x) → ∫₀^x f(t) dt ，∫₀^x f(t) dt 连续）

【注】：可积不一定有原函数。

若 f(x) 是可积的奇函数，则 ∫₀^x f(t) dt 是偶函数且 ∫_a^x f(t) dt 是偶函数。
若 f(x) 是可积的偶函数，则 ∫₀^x f(t) dt 是奇函数。
而 ∫_a^x f(t) dt 看情况：【∫_a^x f(t) dt = ∫_a⁰ f(t) dt + ∫₀^x f(t) dt 】
若 ∫_a⁰ f(t) dt = 0 ，则是奇函数；若 ∫_a⁰ f(t) dt ≠ 0 ，则是非奇非偶函数。
若 f(x) 是可积的周期为 T 的周期函数，若想 ∫₀^x f(t) dt 也是周期为 T 的周期函数，当且仅当 f(x) 在一个周期上积分为 0 ，即 ∫₀^T f(t) dt = 0 。

3）f(x) 连续

【注】：连续一定有原函数。

若 f(x) 是连续的奇函数，则全体原函数都是偶函数。
若 f(x) 是连续的偶函数，则只有一个原函数是奇函数。

【总结】：若 f(x) 连续

∫_a^x f(t) dt	f(x)	f’(x)
偶函数	奇函数	偶函数
仅 ∫₀^x f(t) dt 是奇函数	偶函数	奇函数
若 ∫₀^T f(t) dt = 0 ，则为周期函数	周期函数	周期函数

4）计算定积分的技巧

定积分的奇偶性：（偶倍奇零）
若 f(x) 为奇函数，则 ∫_-a^a f(x) dx = 0
若 f(x) 为偶函数，则 ∫_-a^a f(x) dx = 2·∫₀^a f(x) dx

【注】：对称区间下：∫_-a^a f(x) dx = ∫₀^a [f(x)+f(-x)] dx 。

定积分的周期性：
设 f(x) 是以 T 为周期的连续函数，a 为任意实数，则 ∫_a^a+T f(x) dx = ∫₀^T f(x) dx = ∫_-T/2^T/2 f(x) dx 。
∫₀^π/2 f(sinx) dx = ∫₀^π/2 f(cosx) dx【令 t = π/2 - x】
∫₀^π [x·f(sinx)] dx = (π/2)·∫₀^π f(sinx) dx【令 t = π - x】
要点在于：区间再现公式

4. 例题

二、积分的综合题

1. 变限积分求导

1）变限积分求导公式

(∫_φ(x)^ψ(x) f(t) dt)’ = f[ψ(x)] · ψ’(x) - f[φ(x)] · φ’(x)

【注】：若 ∫_a^x f(■) dt 的 ■ 中含有上限 x ，则需要先换元。

例如：∫₁² f(x+t) dt ，令 u = x + t ，原式 = ∫_x+1^x+2 f(u) du ，进一步有：(∫₁² f(x+t) dt)’ = (∫_x+1^x+2 f(u) du)’ = f(x+2) - f(x+1) 。

2）例题

2. 变限积分求极限

1）方法

洛必达法则、等价无穷小替换、积分中值定理等。（需要观察题目所给信息灵活配凑，必要时先进行换元）

2）易错点

题目若只给出 f(x) 连续，且当 x → 0 时求 lim (∫₀^x f(t) dt)/x² ，利用洛必达法则可以得到 lim f(x)/(2x) ，但是不能继续使用洛必达法则！即不能出现 lim f’(x)/2 。
（因为题目只给出 f(x) 连续，f(x) 是否可导未知）
题目若只给出 f(x) 可导，但未说明导函数在某点（例如 x = a）处连续，则不可以出现 lim_x→a f’(x) 。因为 lim_x→a f’(x) = f’(a) ，但 f’(x) 在 x = a 处是否连续未知。
∫₀^x (x-t)·f(t) dt = x·∫₀^x f(t) dt - ∫₀^x t·f(t) dt 。

无法继续使用洛必达法则时，可以利用积分中值定理进行处理。

【拓展】：

积分中值定理：若 f(x) 在 [a, b] 上连续，则 ∫_a^b f(x) dx = (b - a) · f(ξ) ，其中 a < ξ < b 。（去掉积分限的重要方法）
广义的积分中值定理：若 f(x) , g(x) 在 [a, b] 上连续，且 g(x) 不变号，则 ∫_a^b f(x) · g(x) dx = f(ξ) · ∫_a^b g(x) dx ，其中 a < ξ < b 。

3）例题

3. 变限积分求定积分

1）方法

分部积分（往后凑）
例如：∫_a^b x·f(x) dx = (1/2)·∫_a^b f(x) dx² = (1/2)·[x²·f(x)|_a^b - ∫_a^b x² df(x)]
交换积分顺序

2）例题

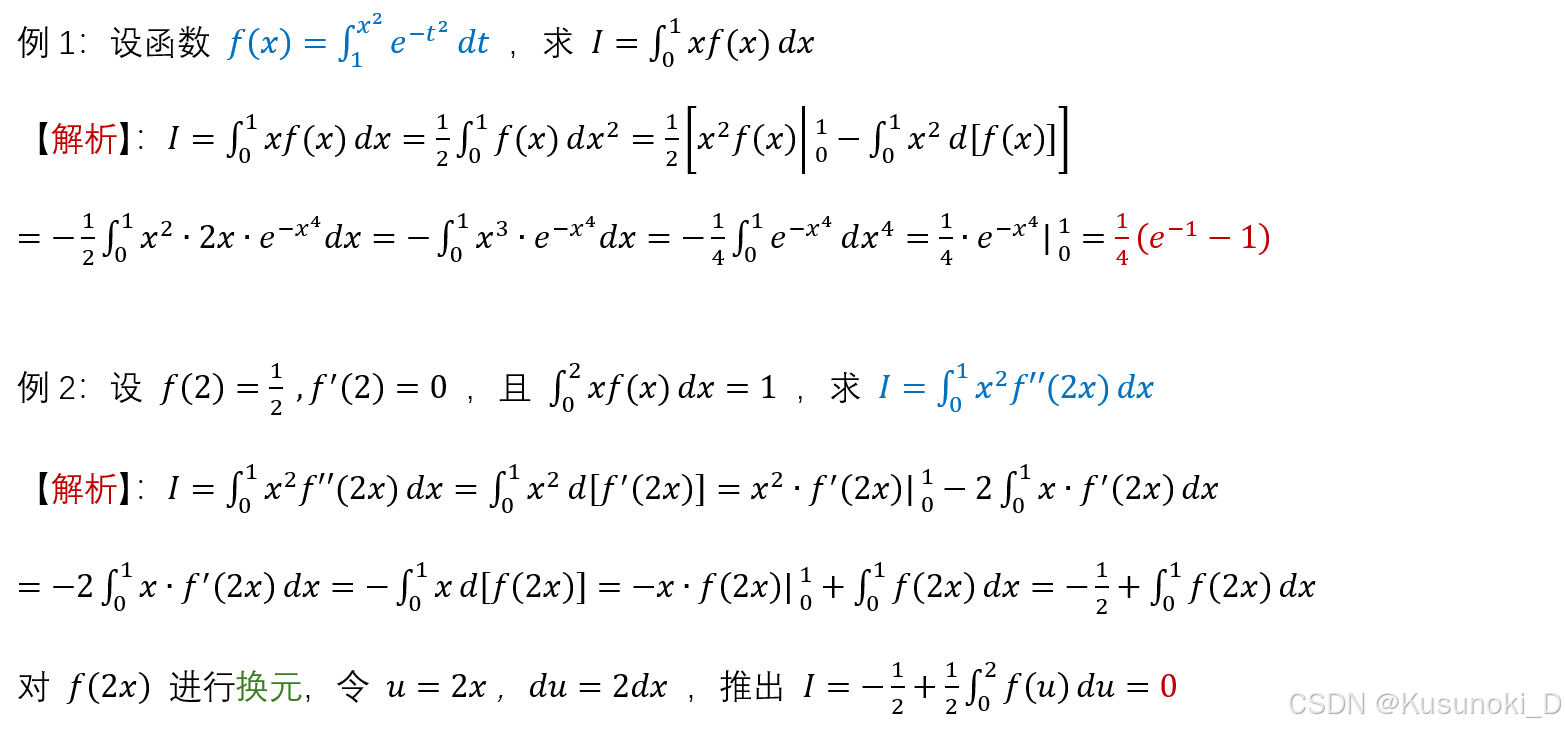
4. 不定积分求原函数

求不定积分的原函数需要注意：原函数天然连续。

下面举一个例子：

三、定积分的定义

1. 定积分的几何意义

定积分的几何意义为：函数 f (x) 在区间 [a, b] 上的曲线下面积

lim_n→∞ (步长)·∑_下限^上限 f(■) = ∫_{区间长度最小值}^{区间长度最大值} f(x) dx

通过 ∑ 的上下限计算出区间长度（将上下限分别带入 f(■) 中）和步数（上限减下限）；
计算步长（步长 = 区间长度 / 步数）。

下面举几个例子：

2. 例题

四、定积分比大小

1. 积分区间相同（比较被积函数大小）

比较被积函数大小时，需要事先处理被比较的式子，使得它们的分子或分母有一个是相同的。
嵌套函数/复合函数：若嵌套单增函数，则不改变不等号的方向；若嵌套单减函数，则改变不等号的方向。
【例如】：在 0 < x < π/2 上有 x > sinx ，则必有 ln(x) > ln(sinx) 、e^x > e^sinx 、cosx < cos(sinx) 等。
常考的不等式需要牢记。
(2/π)x < sinx < x < tanx（0 < x < π/2）
x/(1+x) < ln(1+x) < x（x > 0）
e^x ≥ x + 1（当且仅当 x = 0 时取等号）
除了利用常见的不等式，还可以构造新的函数，通过求导判断其单调性。
【例如】：ln(1+x) 与 (x/2) 在 [0, 1] 上谁大谁小？构造 F(x) = ln(1+x) - (x/2) ，有 F’(x) = 1/(1+x) - (1/2) ，在 [0, 1] 上 F’(x) ≥ 0 ，可得 F(x) 在区间内单调递增，F(x) > F(0) = 0 ，即 ln(1+x) > (x/2) 。
比较 cosx 与 sinx 时，可以画图判断，在 0 < x < π/2 上 sinx 单调递增、cosx 单调递减。
观察积分区间，若上下限互为相反数，考虑是否可以使用 “偶倍奇零” 。
若 f(x) 为偶函数，则 ∫_-a^a f(x) dx = 2·∫₀^a f(x) dx ；若 f(x) 为奇函数，则 ∫_-a^a f(x) dx = 0 。

例题：比较 I₁ = ∫₀^π/2 sin(sinx) dx 、I₂ = ∫₀^π/2 cos(sinx) dx 、I₃ = 1 的大小。
答案：I₂ > I₃ > I₁ 。
【解析】：已知 ∫₀^π/2 sinx dx = ∫₀^π/2 cosx dx = 1 且在 [0, π/2] 上 x > sinx ，在 0 < x < π/2 上 sinx 单调递增、cosx 单调递减，因此有 sinx > sin(sinx) 、cosx < cos(sinx) 。

2. 被积函数相同（积分区间不同）

1）画图法（小题）

方法：在被积函数中找出在区间内“有正有负”的函数，并画出它的图像。

例如：比较 I₁ = ∫₀^π e^x·sinx dx 、I₂ = ∫₀^2π e^x·sinx dx 、I₃ = ∫₀^3π e^x·sinx dx 的大小时，由于在 [0, 3π] 内 e^x 恒正，而 sinx 有正有负，因此画出 sinx 的图像（下图黑色部分）。

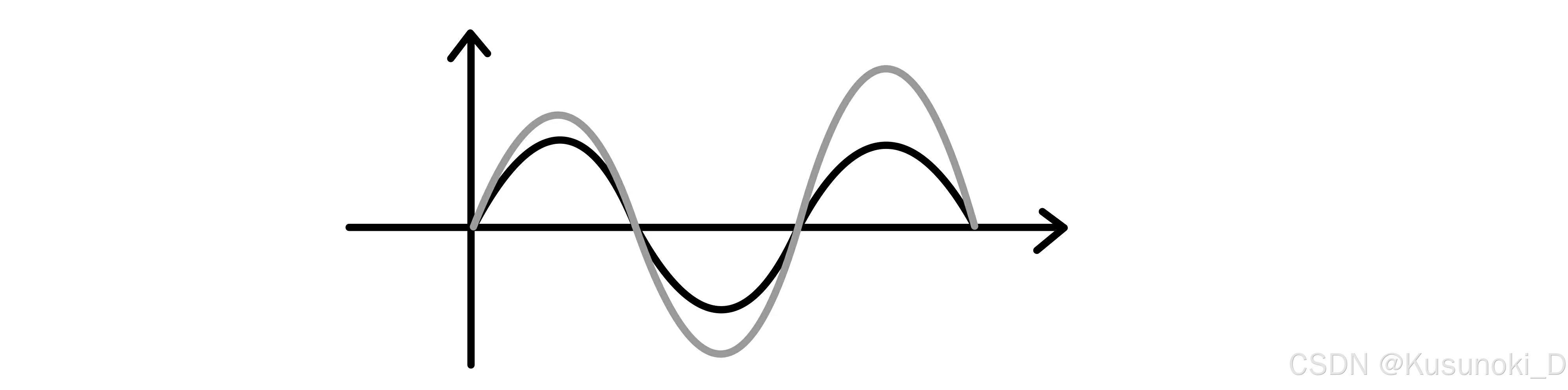
e^x 恒正且在 [0, 3π] 内 ≥ 1 ，因此可以看作纵向拉高了图像，且 x 越大拉的越高，大概图像如上图灰色部分所示。可以看出 I₁ > 0 ，I₂ = I₁ + ∫_π^2π e^x·sinx dx < I₁ ，I₃ = I₁ + I₂ + ∫_2π^3π e^x·sinx dx > I₁ ，即 I₃ > I₁ > I₂ 。

2）拆分法（大题）

方法：

划分出正负区间并拆开；
换元，使拆开后的每个积分的积分区间一致（统一上下限）；
提取公因式，比较大小。

例如：比较 I₁ = ∫₀^π e^x·sinx dx 、I₂ = ∫₀^2π e^x·sinx dx 、I₃ = ∫₀^3π e^x·sinx dx 的大小。

I₁ 中的被积函数在 [0, π] 内恒正，因此不用处理；
I₂ = ∫₀^π e^x·sinx dx + ∫_π^2π e^x·sinx dx ，
换元：令 t = x - π ，有 ∫_π^2π e^x·sinx dx = -∫₀^π e^t+π·sint dt ，
提取：I₂ = ∫₀^π (e^x - e^x+π)·sinx dx < ∫₀^π e^x·sinx dx = I₁ ；
I₃ = ∫₀^π e^x·sinx dx + ∫_π^2π e^x·sinx dx + ∫_2π^3π e^x·sinx dx ，
换元：令 t = x - 2π ，有 ∫_2π^3π e^x·sinx dx = ∫₀^π e^t+2π·sint dt ，
提取：I₃ = ∫₀^π e^x·sinx dx - ∫₀^π e^x+π·sinx dx + ∫₀^π e^t+2π·sint dt = ∫₀^π (e^x - e^x+π + e^t+2π)·sinx dx > ∫₀^π e^x·sinx dx = I₁ ；可得：I₃ > I₁ > I₂ 。

3）例题

① ∫₀^2π e^sint·sint dt（）0【>】

② ∫₀^2π sint/√t dt（）0【>】

③ 当 f’(x) < 0 时，∫_-π^π f(x)·sinx dx（）0【<】

④ 当 f”(x) > 0 时，∫_-π^π f(x)·cosx dx（）0【<】

第 ④ 题的解析：

五、反常积分判敛

1. 反常积分的概念

1）反常积分的定义

定积分：区间有限 + 函数有界。

反常积分：又叫广义积分，是对普通定积分的推广，指含有无穷上限 / 下限，或者被积函数含有瑕点的积分，前者称为无穷限广义积分（无穷区间上的反常积分），后者称为瑕积分（又称无界函数的反常积分）。

2）瑕点的定义

瑕点：如果函数 f(x) 在点 a 的任意一个去心邻域内无界，那么点 a 称为函数 f(x) 的瑕点（也称无界间断点），简单来说瑕点是指被积函数在邻域内无界的点。

反常积分积分限中间有瑕点一定要分开计算。若瑕点 c ∈ (a, b) 时：∫_a^b f(x) dx = ∫_a^c f(x) dx + ∫_c^b f(x) dx 。

【注】：∫_a^c f(x) dx 与 ∫_c^b f(x) dx 都收敛时 ∫_a^b f(x) dx 才收敛，但凡 ∫_a^c f(x) dx 与 ∫_c^b f(x) dx 其中有一个发散，∫_a^b f(x) dx 就发散。

2. p 积分必背结论

常见的四种模型：1/x^p 、ln^qx/x^p 、1/(x^p·ln^qx) 、(lnx)^q 。

3. 敛散性的判别方法（比较审敛法）

还可以直接利用反常积分定义计算来判别敛散性。
例如：∫₀^+∞ x·e^-x dx = -∫₀^+∞ x d(e^-x) = -x·e^-x|₀^+∞ + ∫₀^+∞ e^-x dx = -(x+1)·e^-x|₀^+∞ = 1 ，因此收敛。

当反常积分不易计算时，可将被积函数等价成 1/x^p 或 1/(x-a)^p 的形式，利用比较审敛法（极限形式）的及 p 积分的性质进行判别。

【注】：比较审敛法有极限和不等式两种形式，一般极限形式更实用！

【极限法记忆】：若 lim_x→+∞ f(x) / 收敛 = 0 ，则 f(x) 收敛；若 lim_x→+∞ f(x) / 发散 = ∞ ，则 f(x) 发散。

1）无穷区间

无穷区间的反常积分比较审敛法（极限形式）
无穷区间的反常积分比较审敛法（不等式形式）

【总结】：

2）无界函数

无界函数的反常积分比较审敛法（极限形式）
无穷限的反常积分比较审敛法（不等式形式）

【总结】：

4. 含有对数函数的反常积分

【总结】：

当 x → +∞ 或 x → 0⁺ 时，lnx 在分子处（lnx/x^p）可以不用看，即 lnx/x^p 与 1/x^p 同敛散。
使用等价无穷小替换：x → 0 时 ln(1+x) ~ x ；x → 1 时 lnx ~ x-1 。
当 a 为一个确切的值时，∫₀^a (lnx)^k dx 一定收敛。
证明：为什么 ∫₀¹ (lnx)¹⁰⁰ dx 收敛？
已知 lim_x→0+ (lnx)¹⁰⁰/x^-1/2 = lim_x→0+ √x·(lnx)¹⁰⁰ = 0 ，因为 ∫₀¹ 1/√x dx 收敛，可以得出 ∫₀¹ (lnx)¹⁰⁰ dx 收敛（“大收小收”）。

1）结论 1

2）结论 2

5. 含有指数函数的反常积分

6. 其他结论

绝对收敛的性质：设函数 f(x) 在 [a, +∞) 上连续，若 ∫_a^+∞ |f(x)| dx 收敛，则 ∫_a^+∞ f(x) dx 收敛。

六、反常积分计算

1. 反常积分的四则运算（加减法）

∫_a^+∞ [f(x)±g(x)] dx = ∫_a^+∞ f(x) dx ± ∫_a^+∞ g(x) dx

【注】：上式只有 ∫_a^+∞ f(x) dx 与 ∫_a^+∞ g(x) dx 都收敛时才可拆开计算。

【重点】：拆成两个反常积分时，要注意拆分后每个积分的敛散性。（只有都收敛才可以拆分！）

【方法】：若不可拆开计算时，可按整体求不定积分（g(x) = ∫ f(x) dx），再统一代值计算（∫_a^+∞ f(x) dx = lim_x→+∞ g(x) - lim_x→a+ g(x)）。

2. 找瑕点拆区间

若瑕点位于区间端点，则求极限；若瑕点位于区间内部，则拆区间。

3. 分部积分法

使用分部积分时，要注意每个部分的敛散性。

需要注意 ln ，最后一步求极限时 ln 往往要合并。

4. 换元法

换元后，有时可将反常积分转化为定积分。

七、积分的几何应用

1. 平面曲线弧长

2. 求平面图形面积

1）直角坐标系

2）参数方程

【例题】：

① 求由平摆线的一拱与 x 轴所围平面图形的面积。（S = 3πa²）
平摆线：x = a·(t-sint) ；y = a·(1-cost)（a > 0）
② 求星形线图形围成的面积。（S = (3/8)·πa²）
星形线：x = a·cos³t ；y = a·sin³t

3）极坐标系

【例题】：

① 求伯努利双扭线 r² = a²·cos2θ 围成的图形面积。（S = a²）
② 求对数螺线 r = e^θ（0 ≤ θ ≤ π）及射线 θ = 0 和 θ = π 所围成平面图形的面积。（S = (1/4)·(e^2π-1)）

3. 求旋转体体积

1）直角坐标系

【总结】：公式记忆

y = y(x) 绕 x 轴旋转：V_x = π·∫_a^b y²(x) dx
x = x(y) 绕 y 轴旋转：V_y = π·∫_c^d x²(y) dy
y = y(x) 绕 y 轴旋转：V_y = 2π·∫_a^b x·y(x) dx
x = x(y) 绕 x 轴旋转：V_x = 2π·∫_c^d y·x(y) dy
【通用】绕直线旋转：V = 2π·∫∫_D r(x,y) dσ
其中 r(x,y) 为点 (x,y) 到直线 L 的距离，即 r(x,y) = |ax+by+c| / √(a²+b²)

2）参数方程

令 x = x(t) ，用 y(t) 代替 y ，用 x(t) 代替 x 。核心在于换元（换元有三换）。

【例题】：

① 求由平摆线与 x 轴所围平面图形分别绕 x 轴和 y 轴旋转一周所得旋转体的体积。
（V_x = 5·π²a³ 、V_y = 6·π³a³）
平摆线：x = a·(t-sint) ；y = a·(1-cost)（a > 0）
② 求星形线图形围成的区域绕 x 轴旋转一周所得旋转体的体积。（V = (32/105)·πa³）
星形线：x = a·cos³t ；y = a·sin³t

3）极坐标系

求旋转体体积有通用公式：V = 2π·∫∫_D r(x,y) dσ 。

一般绕极轴旋转即是绕 x 轴旋转，因此公式变为 V = 2π·∫∫_D y(x) dσ ，在极坐标中 x = r·cosθ 、y = r·sinθ ，可得 V = 2π·∫_α^β sinθ dθ∫_a^b r·r dr 。

【例题】：

① 求对数螺线 r = e^θ（0 ≤ θ ≤ π）及射线 θ = 0 和 θ = π 所围成平面图形绕极轴旋转一周所得旋转体的体积。（V = (π/15)·(e^3π+1)）
② 求心形线 r = 4·(1+cosθ) 与射线 θ = 0 和 θ = π/2 所围成平面图形绕极轴旋转一周所得旋转体的体积。（V = 160π）

4. 旋转体的侧面积

【总结】：

5. 质心形心公式

6. 其他技巧

1）常考图形

伯努利双扭线：① (x²+y²)² = a²·(x²-y²) ；② (x²+y²)² = 2a²·xy 。

2）古尔丁定理

八、积分等式和不等式

1. 积分的重要性质

比较定理：若 f(x) ≤ g(x) ，x ∈ [a, b] ，则 ∫_a^b f(x) dx ≤ ∫_a^b g(x) dx 。
定理核心：比较开区间内被积分函数间的大小（直接比、间接比）。

重点不等式：（1）e^x - 1 ≥ x（当且仅当 x = 0 时取等号）；
（2）ln(1 + x) ≤ x（当且仅当 x = 0 时取等号）；
（3）tanx > x > sinx（0 < x < π/2）；
（4）x > sinx（x > 0）；
（5）1/(1+x) < ln[1+(1/x)] < 1/x（x > 0）；
（6）x/(1+x) < ln(1+x) < x（x > 0）。

推论：|∫_a^b f(x) dx| ≤ ∫_a^b |f(x)| dx 。（还需要牢记不等式：|a ± b| ≤ |a| + |b|）
积分中值定理：设 f(x) 在 [a, b] 上连续，则至少存在一点 ξ ∈ (a, b)，使得 ∫_a^b f(x) dx = (b - a) · f(ξ) 。
【注】：去掉积分限的重要方法。
广义的积分中值定理：若 f(x) 与 g(x) 在 [a, b] 上连续，且 g(x)不变号，则至少存在一点 ξ ∈ (a, b)，使得 ∫_a^b f(x) · g(x) dx = f(ξ) · ∫_a^b g(x) dx 。
函数的平均值：称 ∫_a^b f(x) dx / (b-a) 为函数 f(x) 在区间 [a, b] 上的平均值。
若 f(x) 在区间 [a, b] 上连续，则 m(b-a) ≤ ∫_a^b f(x) dx ≤ M(b-a) ，其中 m, M 分别为 f(x) 在 [a, b] 上的最小值与最大值。

2. 放缩 / 夹逼准则

【方法步骤】：
第 0 步：利用积分中值定理或积分第一中值定理进行预处理；
（例如：lim_n→∞ ∫_a^b f(xⁿ)·g(x) dx = g(ξ_n)·lim_n→∞ ∫_a^b f(xⁿ) dx ，ξ_n ∈ [a, b]）
第 1 步：对积分进行放缩（利用上下限、常见不等式、最值等）；
（例如：∫_a^b φ(xⁿ) dx ≤ ∫_a^b f(xⁿ) dx ≤ ∫_a^b ψ(xⁿ) dx）
第 2 步：构造不等式，并算出好积的积分；
（例如：lim_n→∞ ∫_a^b φ(xⁿ) dx = lim_n→∞ ∫_a^b ψ(xⁿ) dx = 0）
第 3 步：利用夹逼准则计算出难积的积分。
（例如：g(ξ_n)·lim_n→∞ ∫_a^b f(xⁿ) dx = lim_n→∞ ∫_a^b f(xⁿ)·g(x) dx = 0）

∫_a^b α(x) dx ≥ ∫_a^b β(x) dx ⇔ ∫_a^b [α(x)-β(x)] dx ≥ 0 。

1）利用上下限放缩

【例题】：求极限 lim_n→∞ ∫₀¹ xⁿ·√(1+x²) dx 。

【解析】：

方法 1：通过放缩利用 “夹逼准则” 。

已知 0 ≤ x ≤ 1 ，可得 ∫₀¹ xⁿ dx ≤ ∫₀¹ xⁿ·√(1+x²) dx ≤ √2·∫₀¹ xⁿ dx 。又有：
（a）lim_n→∞ ∫₀¹ xⁿ dx = lim_n→∞ [xⁿ⁺¹/(n+1)]|₀¹ = lim_n→∞ [1/(n+1)] = 0 ；
（b）lim_n→∞ √2·∫₀¹ xⁿ dx = √2·lim_n→∞ [xⁿ⁺¹/(n+1)]|₀¹ = √2·lim_n→∞ [1/(n+1)] = 0 。
由夹逼准则可得 lim_n→∞ ∫₀¹ xⁿ·√(1+x²) dx = 0 。

方法 2：利用 “推广的积分中值定理” 。

∫₀¹ xⁿ·√(1+x²) dx = √(1+ξ_n²)·∫₀¹ xⁿ dx = √(1+ξ_n²)/(n+1) ，其中 0 ≤ ξ_n ≤ 1 ，
有：lim_n→∞ ∫₀¹ xⁿ·√(1+x²) dx = lim_n→∞ [√(1+ξ_n²)/(n+1)] dx = 0 。

【注】：由上述方法 2 得出以下结论
I、如果需要和积分中值定理相结合的话，往往利用积分中值定理把不带 n 的部分（例如上例中的 √(1+x²) ）移到积分号外，把有 n 的部分（例如上例中的 xⁿ ）留在积分内，算出积分。
II、积分中值定理与 f(x_n) 结合，需要注意此时的 ξ 范围依赖 n ，因此应该写成 ξ_n 。