高等数学（第三章：一元积分学 ① ）

---

一、不定积分的计算

1. 常见公式总结

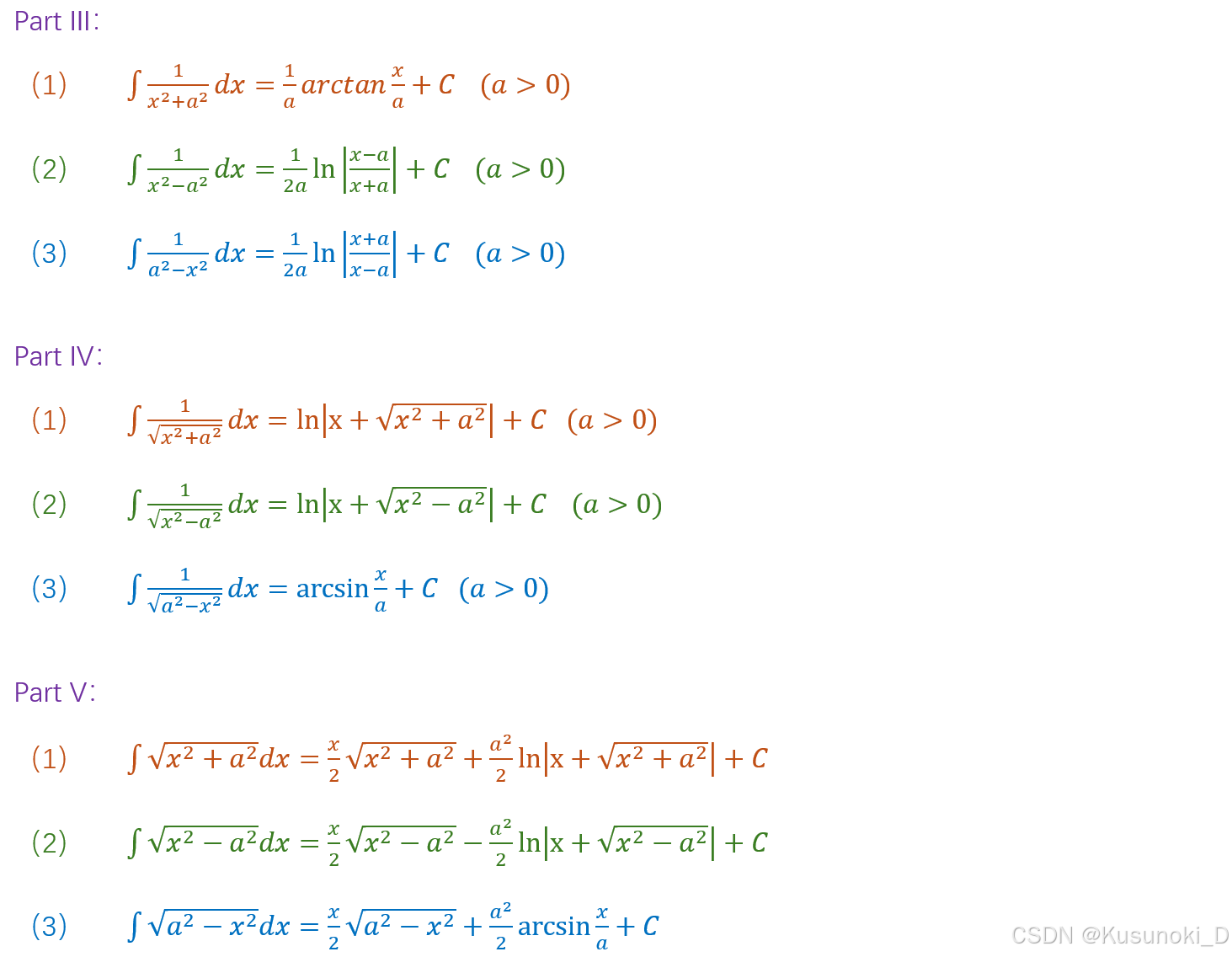
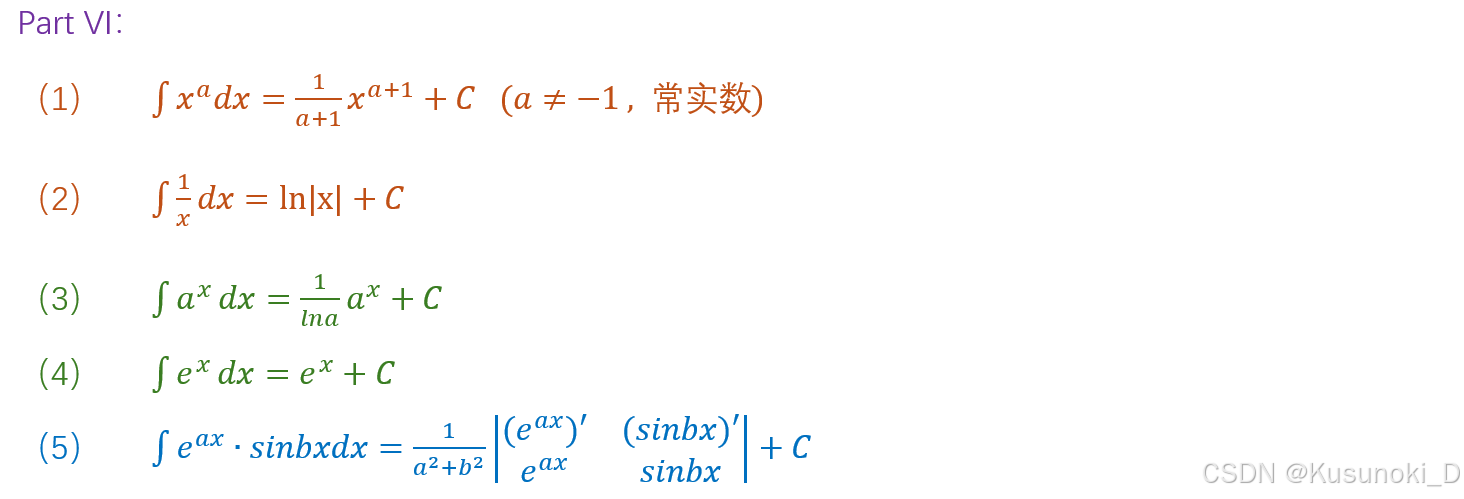
【注】：常用的公式要熟稔于心，实在背不下来的式子要熟练掌握其推导方法。

• 有理式：包括分式和整式，这种代数式中对于字母只进行有限次加、减、乘、除和整数次乘方这些运算，它也可以化为两个多项式的商。

• 无理式：含有关于字母开方运算的代数式称为无理式。

2. 凑微分法

考虑对复杂式子进行求导，去找出和其他式子的联系！

常见的凑微分示例：

【注】：一定不要忘记 +C ！！！

3. 指数函数

1）做题技巧（预处理）

• I、去指数：如果被积函数 f(x) = g(e^x) ，令 e^x = t ，则 ∫f(x)dx = ∫g(e^x)dx = ∫[g(t)/t]dt ，达到去指数的作用。

• II、添项减项（“1”的处理）。

• III、若为分式，则可以考虑上下同除 e^x 或 e^2x 等。

2）示例

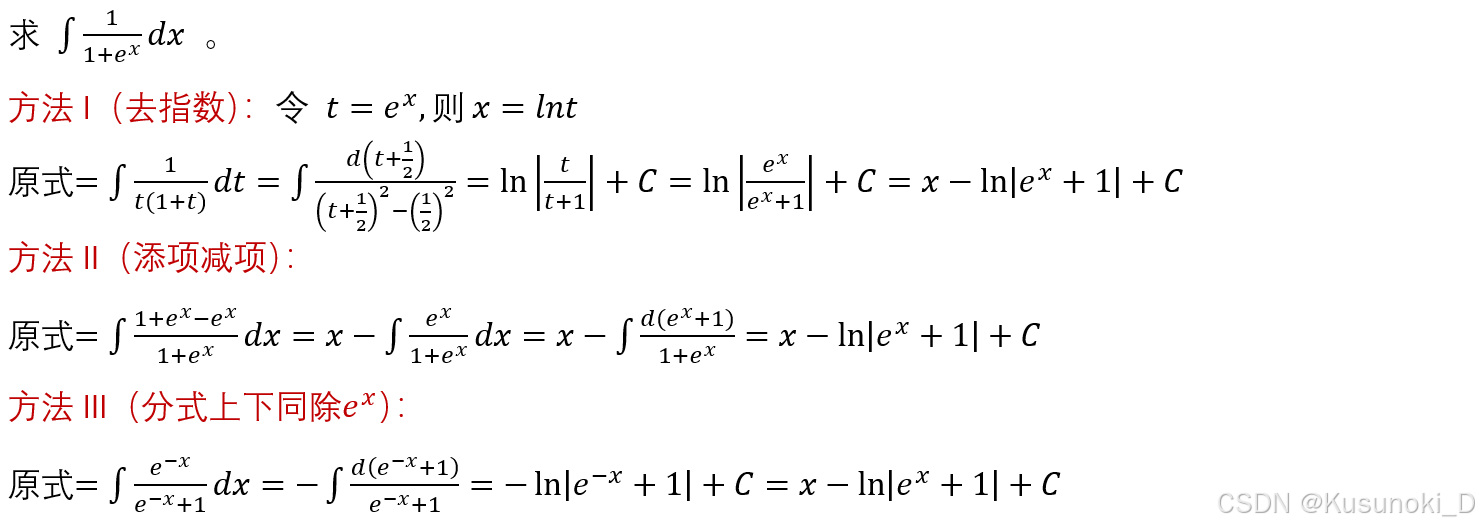
4. 无理函数（根式代换和三角换元）

该类积分的处理思想就是去根号变成有理函数的积分（根式代换）。

• 如果被积函数中含有 ⁿ√(ax+b) ，则令 ⁿ√(ax+b) = t ；

• 如果被积函数中同时含有 ⁿ√(ax+b) , ^m√(ax+b) ，则令 ^l√(ax+b) = t（l 为 m 和 n 的最小公倍数）；

• 如果被积函数中含有 ⁿ√(ax+b)/(cx+d) ，则令 ⁿ√(ax+b)/(cx+d) = t ；

• 如果被积函数中含有 √(ax²+bx+c) ，此时有两种处理方法去根号有理化：欧拉代换和三角代换。

1）欧拉代换

2）三角代换

见到 “平方 ± 平方” 想到三角换元。
重点在于：怎么换元？怎么换回来？

• sin²x + cos²x = 1 ；tan²x + 1 = sec²x ；cot²x + 1 = csc²x 。

• 如果出现了 √(1-x²) 和 arcsinx ，则令 arcsinx = t ，得 x = sint ，√(1-x²) = cost（去根号）；

• 如果出现了 √(1+x²) 和 arctanx ，则令 arctanx = t ，得 x = tant ，√(1+x²) = sect 。

5. 三角有理式

1）偶降奇提

2）类型总结

• ∫ 1/(1+sinx) dx 型
  ① 平方差公式：
  (1 + cosx) · (1 - cosx) = 1 - cos²x = sin²x ；
  (1 + sinx) · (1 - sinx) = 1 - sin²x = cos²x 。
  ② 倍角公式：
  sinx = 2 · sin(x/2) · cos(x/2) ；
  cosx = 2 · cos²(x/2) - 1 = 1 - 2 · sin²(x/2) 。

• ∫ 1/(sinx+cosx) dx 型
  辅助角公式：（简化分母）
  a·sin(α) + b·cos(α) = (√(a² + b²))·sin[α + arctan(b/a)]（a > 0）；
  a·sin(α) + b·cos(α) = (√(a² + b²))·cos[α - arctan(b/a)]（b > 0）。

• ∫ (asinx+bcosx)/(sinx+cosx) dx 型
  待定系数法：分子拆分为分母与分母的导数之和
  即：asinx+bcosx = A(sinx + cosx) + B(sinx + cosx)’ = (A - B) · sinx + (A + B) · cosx ，
  有 A - B = a 、A + B = b ，解出 A 、B 。

【拓展】：形式待定

• ∫ (px+q)/√(ax²+bx+c) dx 型（a ≠ 0）
  

• ∫ (csinx+dcosx)/(asinx+bcosx) dx 型（a² + b² ≠ 0）
  

• ∫ e^λx·[pcoskx+qsinkx] dx 型
  

• ∫ e^λx·[P₁(x)coskx+P₂(x)sinkx] dx 型
  

• ∫ f(x)/g²(x) dx 型
  

• ∫ f(x)·e^g(x) dx 型
  

3）提前预判

4）齐次同除

若 R(-sinx, -cosx) = R(sinx, cosx) ，或分式的分母齐次，则可使用齐次同除法。

• 分式上下同除 cos²x ；

• 常数变成 cos^-2x = sec²x 、sin²x 变成 tan²x 、cos²x 变成常数；

• sec²x 凑成 d(tanx) ；

• sec²x 变为 tan²x + 1 。

下面举一个例子：

5）万能代换

6）技巧

• 对于三角有理函数，可以利用 “积化和差” 和 “降幂公式” 来实现降次。
  

• “1” 的处理
  ① 添项减项，然后拆分成多个式子进行计算；
  ② sin²x + cos²x = 1 、tan²x + 1 = sec²x 、cot²x + 1 = csc²x 。

6. 分部积分（表格积分法）

1）利用分部积分实现降次（去分母）

特别地，对于形如 ∫(f/g²)dx 的积分，可以考虑强行凑 d(1/g) 得 ∫(-f/g’)d(1/g) 。

2）利用分部积分法产生递推公式

求出递推公式之后，再利用递推公式就可以求出通项公式，一般来讲，题目不会要你求出不定积分的通项公式（因为表达式太复杂了），只要你求出某一项！

求含有 n 的不定积分或定积分如下的一种方法：

• 第一步：利用分部积分法产生递推公式；

• 第二步：利用递推公式推出通项公式。

3）局部利用分部积分法

当整体不好利用分部积分法时，可以考虑对局部利用分部积分法，对其中一部分利用分部积分法然后和另外一部分进行抵消。

4）表格积分法原理及应用

5）技巧

• 常数化简：
  ∫ln(1+x)dx = ∫ln(1+x)d(1+x) = (1+x)·ln(1+x) - ∫1dx（分部积分法）= (1+x)·ln(1+x) - x 。

• 循环积分 ∫(e^ax·sinbx)dx：除了使用分部积分法外，还可以使用公式
  
  【注】：常见的循环积分还有：∫sec³xdx 、√(x²+a²)dx 等。

• 常规积分：常与 “换元” 相结合。
  【注】：换元时令 t = f(x) ，反解出 x = g(t) ，使用分部积分法时，不一定要解出 dx ，转而直接使用分部积分更方便。下面举出一个示例：
  

7. 有理函数

无理函数积分通常的处理手法是：去根号变有理函数的积分；三角有理函数积分通常的处理手法是：去三角变有理函数的积分。所以说有理函数的积分是最要的一部分！

【注】：大家在做题时需要牢记一个小技巧，被积函数中出现了复合函数 f(g(x)) ，一般令内层函数 g(x) = t ，去复合，简化被积函数！

1）有理函数的积分

【总结】：

• 拆假分式（长除法）；
  例如：由于 2x³+x-3 除以 x²+1 得 2x 余 -x-3 ，因此 (2x³+x-3)/(x²+1) = 2x - (x+3)/(x²+1) 。

• 拆真分式（因式分解）+ 定系数。
  ① 分母含 ax+b → A/(ax+b)
  ② 分母含 (ax+b)² → A₁/(ax+b) + A₂/(ax+b)²
  ③ 分母含 ax²+bx+c → (Ax+B)/(ax²+bx+c)
  ④ 分母含 (ax²+bx+c)² → (Ax+B)/(ax²+bx+c) + (Cx+D)/(ax²+bx+c)²
  定系数的方法有：通分列方程组来待定系数、留数法、求谁挡谁代谁、代特殊值、极限法。

【注】：分母为 ax²+bx+c 时，若 Δ = b²-4ac > 0 ，则化为平方和，例如 (Ax+B)² ；若 Δ < 0 ，则拆解为 (Cx+D)/(ax²+bx+c) 。

“通分来待定系数” 的方法对于复杂式子来说计算麻烦，“留数法” 大家感兴趣的话可以自行查找资料学习。下面介绍使用起来比较简单方便的 “求谁挡谁代谁” 法、 “代特殊值” 法和 “极限” 法。

I、“求谁挡谁代谁” 法

假设把 A/(ax+b)(cx+d) 拆分为 B/(ax+b) + C/(cx+d) 。“求谁挡谁代谁” 的意思是：挡住原式中被求分子的分母部分（例如求 B 值时，原式变为 A/■(cx+d) ），将使得该分母为 0 的值（ ax+b=0 得到 x=-b/a ）代入被遮挡的原式中（ x=-b/a 代入 A/■(cx+d) ），得到的值就是被求分子的值（ B=A/[c·(-b/a)+d] ）。

II、“代特殊值” 法

假设把 Ax/(ax+b)(cx²+dx+e) 拆分为 B/(ax+b) + (Cx+D)/(cx²+dx+e) 。B 的值可以通过 “求谁挡谁代谁” 法进行求解，求出 B 后可以通过代入特殊值，例如 x = 0 求出 D 的值，即：0 = B/b + D/e ，从而求出 D = -B·e/b 。

III、“极限” 法

假设把 Ax/(ax+b)(cx²+dx+e) 拆分为 B/(ax+b) + (Cx+D)/(cx²+dx+e) 。B 的值可以通过 “求谁挡谁代谁” 法进行求解，求出 B 后将等式两边同时乘 x ，即 Ax²/(ax+b)(cx²+dx+e) = Bx/(ax+b) + (Cx²+Dx)/(cx²+dx+e) ，当 x → +∞ 时，等式两边取极限得到：0 = B + C/c ，从而求出 C = -B·c 。

下面举几个例子：

【注】：需要有 “广义化” 的思想，例如：求 ∫1/[x²(1+x²)(1-x²)]dx 时可以把 x² 看成一个整体 u ，那么 1/[x²(1+x²)(1-x²)] 可以看成 1/[u(1+u)(1-u)] ，从而拆解为 A/u + B/(1+u) + C/(1-u) ，用 “求谁挡谁代谁” 法求出 A、B、C 的值后，再将 u 换成 x² 即可。1/[x²(1+x²)(1-x²)] = 1/x² - (1/2)/(1+x²) + (1/2)/(1-x²) 。

【总结】：

• 分子为常数，分母的最高次数为 2：∫C/(ax²+bx+c)
  方法：将分母 ax²+bx+c 转换为 (dx+e)²+f² 的形式，然后套用公式 ∫1/(x²+a²)=(1/a)arctan(x/a)+C。

• 分子的最高次数为 1 ，分母的最高次数为 2：∫(Ax+B)/(ax²+bx+c)
  方法：A·x + B = C₁·(ax²+bx+c)’ + C₂ = 2aC₁x + bC₁ + C₂

• 分子为常数，分母为 (▲)²：∫C/(ax+b)²

【拓展】：常见的恒等变形

• 添项减项，以迎合分母。例如：∫1/(1+e^x)dx = ∫(1+e^x-e^x)/(1+e^x)dx = x-∫e^x/(1+e^x)dx 。

• 分式上下同乘或同除。例如：齐次同除、去根号、∫(x²+1)/(x⁴+1)dx 等。

• “1” 的处理。

2）倒代换

8. 组合积分法

难点在于：构造一个新积分 J 以及构造出线性组合的系数。

【总结】：

• 三角有理式：∫(c·sinx+d·cosx)/(a·sinx+b·cosx)dx 、∫(c·sin²x+d·cos²x)/(a·sinx+b·cosx)dx 、∫(a·sin³x+b·cos³x)/(sinx+cosx)dx
  需要利用到：sin²x + cos²x = 1 、平方差公式、立方和公式。
  【a³+b³=(a+b)·(a²-ab+b²) 、a³-b³=(a-b)·(a²+ab+b²)】。

• 指数有理式：∫(c·e^x+d·e^-x)/(a·e^x+b·e^-x)dx

• 有理函数

例题：

二、定积分的计算

1. 牛顿-莱布尼兹公式

牛顿-莱布尼兹公式：如果 F(x) 是连续函数 f(x) 在区间 [a, b] 上的一个原函数，则：

∫_a^b f(x) dx = F(x)|_a^b = F(b) - F(a)

【注】：f(x) 在区间内必须是连续函数！例如：∫_-1¹ (1/x) dx = ln|x||_-1¹ = 0 是错误的，因为 x = 0 对于 1/x 来说是一个无定义的点，因此在区间 [-1, 1] 上 1/x 不是连续函数。

正确的做题方法是什么？

• ① 若无定义的点在区间端点处：正常计算（取极限）；

• ② 若无定义的点在区间内：拆分区间，使无定义的点处于拆分后的区间的端点处。

下面举几个例子：

2. 奇偶性、周期性与几何性质

1）奇偶性（积分上限与积分下限互为相反数）

【注】：对称区间下：∫_-a^a f(x) dx = ∫₀^a [f(x)+f(-x)] dx 。

③ 奇函数 × 奇函数 = 偶函数；偶函数 × 偶函数 = 偶函数；奇函数 × 偶函数 = 奇函数。

④ 复合函数的奇偶性：F(x) = f(g(x)) ，即 y = f(u) , u = g(x)

• 若 f(u) 是奇函数，g(x) 是偶函数，则 F(x) 为偶函数；

• 若 f(u) 是偶函数，g(x) 是奇函数，则 F(x) 为偶函数；

• 若 f(u) 是奇函数，g(x) 是奇函数，则 F(x) 为奇函数；

• 若 f(u) 是偶函数，g(x) 是偶函数，则 F(x) 为偶函数。

复合函数的奇偶性可以利用口诀：“一偶全偶” 来记忆。如果实在没有记住，可以举一些简单例子来佐证，例如：假设 f(u) = u（奇）、g(x) = x²（偶），那么 F(x) = x²（偶）。

2）周期性（积分上限减积分下限等于一个周期）

对称、平移及周期函数在定积分中的应用：

【注】：周期性判断：f(x+T) = f(x)

周期函数在一个周期上的积分值与起点无关，即无论 a 值是多少，最后的积分值都等于 ∫₀^Tf(x)dx ，例如：函数 cos²x 的周期为 π ，有 ∫_π/4^5π/4cos²xdx = ∫₀^πcos²xdx = 2·∫₀^π/2cos²xdx = π/2 。

3）几何性质

• ∫₀^π sinx dx = ∫_-π/2^π/2 cosx dx = 2（ sinx 、cosx 图像中 “一拱” 的面积为 2 ）

• ∫₀¹ √(1-x²) dx = π/4（可以看成 x² + y² = 1 (x, y ≥ 0) 的面积，即 1/4 的半径为 1 的圆面积）

• ∫₀^a √(a²-x²) dx = (π/4)a²（可以看成 x² + y² = a² (x, y ≥ 0) 的面积，即 1/4 的半径为 a 的圆面积）

【拓展】：

√(1-sin2x) = √(sin²x+cos²x-2·sinx·cosx) = √(sinx-cosx)² = |sinx-cosx| ；
同理，√(1-sinx) = |sin(x/2)-cos(x/2)| 。

3. 换元技巧

换元有三换：积分上下限、函数部分、微分部分。

例如：令 t = f(x) 并反解出 x = g(t) ，则 ∫_a^b f(x) dx = ∫_f(a)^f(b) t d[g(t)] 。

下面举几个例子：

• ∫₀^x f(x-t) dt 令 u = x - t ，原式 = ∫_x⁰ f(u) d(x-u) = ∫₀^x f(u) du

• ∫₀^x t·f(x-t) dt 令 u = x - t ，原式 = ∫_x⁰ (x-u)·f(u) d(x-u) = x·∫₀^x f(u) du - ∫₀^x u·f(u) du

• ∫₀^x t·f(x²-t²) dt 令 u = x² - t² ，原式 = (1/2)·∫₀^x2 f(u) du

【换元技巧】：

• ∫₀² √[1-(x-1)²] dx = ∫_-1¹ √(1-x²) dx（令 x - 1 为一个整体）

• ∫₀^x f(t-x) dt = ∫_-x⁰ f(t) dt（令 t - x 为一个整体）

• ∫₀¹ f(t·x) dt = (1/x)·∫₀^x f(t) dt（令 t · x 为一个整体）

• ∫₀^x2 f(t/x) dt = x·∫₀^x f(t) dt（令 t / x 为一个整体）

• ∫₀^π sin(x/2) dx = 2·∫₀^π/2 sin(x) dx（令 x / 2 为一个整体）
  [易错]：∫₀^π sin(x/2) dx = 2·∫₀^π sin(x/2) d(x/2) ≠ 2·∫₀^π sin(t) d(t)

下面举几个例子：

4. 区间再现公式

把 x 换成：上限 + 下限 - x 。如何证明？令 t = a + b - x 即可。

区间再现公式的几何意义：函数 f(x) 与 f(a+b-x) 在区间 [a, b] 上关于 x = (a+b)/2 对称，此时在区间 [a, b] 内，函数 f(x) 与 x 轴围成的面积和 f(a+b-x) 与 x 轴围成的面积是相等的，因此 ∫_a^b f(x) dx = ∫_a^b f(a+b-x) dx 。

【拓展】：

区间再现公式的另一个作用是：消去 x 。

• 当 f(x) = x·g(x)（其中 g(x) 满足 g(x) = g(a+b-x)）时：
  ∫_a^b x·g(x) dx = ∫_a^b (a+b-x)·g(a+b-x) dx = [(a+b)/2]·∫_a^b g(x) dx

• ∫₀^x t·f(x-t) dt 利用区间再现公式为：∫₀^x (x-t)·f(t) dt = x·∫₀^x f(t) dt - ∫₀^x t·f(t) dt 。

【注】：只要原函数不好求，就可以考虑使用区间再现公式。

5. 倒代换公式

6. 利用分部积分法进行降阶与升阶求定积分

【注】：证明 “点火公式” 就用这个方法，利用分部积分法产生递推公式。
例如：I_n = ∫₀^π/2 sinⁿx dx = -∫₀^π/2 sin^n-1x d(cosx) = …（分部积分），最后得到 I_n = [(n-1)/n]·I_n–2 。

7. “葵花点穴手”

• 轴对称：f(a+x) = f(b-x)【对称轴为 x = (a+b)/2】
  在区间 [-a, a] 内的偶函数是轴对称图形，关于 y 轴（x = 0）对称。

• 中心对称：f(a+x) + f(b-x) = c【对称中心为 ((a+b)/2, c/2)】
  在区间 [-a, a] 内的奇函数是中心对称图形，关于 (0, 0) 中心对称。
  注：在任何区间内 y = x 都是中心对称图形。

8. 点火公式

常规版：

进阶版：

9. 分段函数、最值函数求定积分

1）分段函数求定积分

技巧就是：拆分积分区间。必要时可以先对积分进行换元处理。

例如：求 I = ∫₀² f(x-1) dx ，其中：当 x ≥ 0 时 f(x) = A ，当 x < 0 时 f(x) = B 。

【解析】：通过换元可以得到：I = ∫₀² f(x-1) dx = ∫_-1¹ f(x) dx ，然后划分积分区间：I = ∫_-1⁰ f(x) dx + ∫₀¹ f(x) dx = ∫_-1⁰ B dx + ∫₀¹ A dx 。

2）符号函数求定积分

接下来讲带 “绝对值” 符号、“取整” 符号、“最大值最小值” 符号的积分。

• 带绝对值符号的积分：这类积分一般都是要对积分区间进行划分，去绝对值符号。

• 带取整符号：这类积分一般都是要去取整符号。
  例如：令 [2^x] = k ，得 k ≤ 2^x < k+1 ，有 lnk/ln2 ≤ x < ln(k+1)/ln2 ，从而对积分区间进行划分。

• 带最大值最小值符号的积分（本质还是分段函数）：可以结合图形进行处理。

10. 其他技巧

1）定积分的本质是个数

把定积分当作一个常数来看待，比如令 ∫_a^b f(x) dx = A 。

下面举一个例子：

2）有关 ∫₀¹ |t - x| dx 的类型

① 方法：在 ∫₀¹ |t - x| dx 中，x 的取值范围是 [0, 1] ，而 t 的取值范围是 (-∞, +∞) 。可以推断出：

• 在 t < 0 时必有 x > t（即 ∫₀¹ |t - x| dx = ∫₀¹ x - t dx）；

• 在 t > 1 时必有 t > x（即 ∫₀¹ |t - x| dx = ∫₀¹ t - x dx）；

• 而 t ∈ [0, 1] 时，又分为以下两种情况：
  x ∈ [0, t] 时，有 t > x（即 ∫₀^t |t - x| dx = ∫₀^t t - x dx）；
  x ∈ [t, 1] 时，有 x > t（即 ∫_t¹ |t - x| dx = ∫_t¹ x - t dx）。

② 例题：

3）循环公式