MPNet: Masked and Permuted Pre-training for Language Understanding（2020-4-20）

模型介绍

BERT采用掩模语言建模(MLM)进行预训练，是最成功的预训练模型之一。由于BERT忽略了预测的 token 之间的依赖关系，XLNet引入了排列语言建模(PLM)进行预训练，以解决这个问题。然而，XLNet并没有利用一个句子的全部位置信息，因此在预训练和微调之间存在位置差异。

MPNet，一种新的预训练方法，既继承了BERT和XLNet的优点，又避免了它们的局限性。MPNet通过排列语言建模(与BERT中的MLM相比)利用预测标记之间的依赖关系，并将辅助位置信息作为输入，使模型看到完整的句子，从而减少位置差异(与XLNet中的PLM相比)。

MPNet既解决了MLM和PLM的问题，又继承了它们的优势：

• 通过置换语言建模考虑了预测标记之间的依赖关系，从而避免了BERT问题；
• 以所有token的位置信息作为输入，使模型看到所有token的位置信息，从而缓解了XLNet的位置差异。

模型改进

预训练方法的关键是为模型训练设计自监督的任务/目标，利用大型语言语料库进行语言理解和生成。对于语言理解，BERT中的屏蔽语言建模(MLM)和XLNet中的排列语言建模(PLM)是两个具有代表性的目标。

MLM in BERT

BERT是最成功的自然语言理解预训练模型之一。它采用Transformer作为特征提取器，引入屏蔽语言模型(MLM)和下句预测作为训练目标，学习双向表示。具体而言，给定一个句子 $x=(x_1,x_2,...,x_n)$，MLM随机屏蔽15%的令牌，用一个特殊的符号 $[M]$ 来代替被屏蔽的词。用 $K$ 表示被屏蔽的位置集合，则 $x_K$ 表示被屏蔽的 token 集合，$x_{\setminus K}$ 表示被屏蔽后的句子。在上图中， K = { 2 , 4 } , x K = { x 2 , x 4 } , x ∖ K = { x 1 , [ M ] , x 3 , [ M ] , x 5 } K=\{2,4\},x_K=\{x_2,x_4\},x_{\setminus K}=\{x_1,[M],x_3,[M],x_5\} K={2,4},xK​={x2​,x4​},x∖K​={x1​,[M],x3​,[M],x5​}，MLM通过最大化以下目标函数来预训练模型参数 $\theta$：

PLM in XLNet

排列语言模型(PLM)是在XLNet中提出的，它保留了自回归建模的优点，同时也允许模型捕获双向上下文。给定一个句子 $x=(x_1,x_2,...,x_n)$，长度为 $n$，那么就会有 $n!$ 中可能的排序。用 $Z_n$ 表示集合 { x 1 , x 2 , . . . , x n } \{x_1,x_2,...,x_n\} {x1​,x2​,...,xn​} 的所有排列，对于其中一个排列 $z\in Z_n$，用$z_t$ 表示$z$ 的第 $t$ 个元素以及用 $z_{<t}$ 表示 $z$ 的前 $t$ 个元素。如上图所示， $z=(1,3,5,2,4)$，如果 $t=4$，那么 z t = 2 , x z t = x 2 , z < t = { 1 , 3 , 5 } z_t = 2, x_{z_t} = x_2,z_{<t} =\{1, 3, 5\} zt​=2,xzt​​=x2​,z<t​={1,3,5}。PLM通过最大化以下目标函数来预训练模型参数 $\theta$：

A Unified View of MLM and PLM

Transformer接受 token 及其位置作为输入，并且对这些 token 的绝对输入顺序不敏感，只有当每个token 与句子中其正确的位置相关联时才会如此。如上图所示，对于MLM，左边的输入等于首先排列序列，然后屏蔽最右边的标记（$x_2$和$x_4$在排列序列$(x_1,x_3,x_5,x_2,x_4)$中的右侧）；对于PLM，首先将序列$(x_1,x_2,x_3,x_4,x_5)$排列成$(x_1,x_3,x_5,x_2,x_4)$，然后选择最右边的token $x_2$ 和 $x_4$ 作为右边所示的预测token，和左边的 MLM一样。也就是说，在这个统一视图中，对于MLM和PLM，非掩码 token 放在左侧，而掩码和待预测 token 放在排列序列的右侧。

在这个统一的视图下，可以将MLM的目标函数改写为：

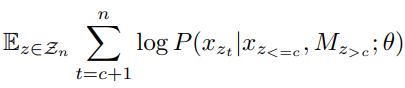
其中，$M_{z_{>c}}$ 表示在位置 $z_{>c}$ 被遮掩的所有 token $[M]$。在上图中， n = 5 , c = 3 , x z < = c = { x 1 , x 3 , x 5 } , z > c = { x 2 , x 4 } , M z > c n=5,c=3,x_{z_{<=c}}=\{x_1,x_3,x_5\},z_{>c}=\{x_2,x_4\},M_{z_{>c}} n=5,c=3,xz<=c​​={x1​,x3​,x5​},z>c​={x2​,x4​},Mz>c​​表示在位置$z_4=2,z_5=4$处被遮掩的两个 token。可以将PLM的目标函数写成：

可以发现MLM和PLM有着相似的数学公式，在条件$P(x_{z_t}|\cdot ;\theta )$部分略有不同，MLM的条件为 $x_{z_{<=c}},M_{z_{>c}}$，而PLM的条件为 $x_{z_{<t}}$。

Proposed Method

MPNet的训练目标函数为：

可以看到，MPNet的条件为 $x_{z_{<t}}$（当前预测 token 之前的 token），而不仅仅是MLM中的非预测 token $x_{z_{<=c}}$，和PLM相比，MPNet携带了更多的信息（在位置 $z_{>c}$ 的掩码符号 $[M]$）作为输入。虽然目标看起来很简单，但要有效地实现这个模型是很有挑战性的。因此，使用几个关键的技巧。

Input Tokens and Positions

用一个例子来阐述MPNet输入的token 和位置。对于一个长度 $n=6$ 序列 $x=(x_1,x_2,...,x_6)$，然后随机的排列序列，得到一个排列顺序 $z=(1,3,5,4,6,2)$ 和一个排列序列 $x_z=(x_1,x_3,x_5,x_4,x_6,x_2)$。未预测的长度为 $c=3$，序列为 $x_{z_{<=c}}=(x_1,x_3,x_5)$，需要预测的序列为 $x_{z>c}=(x_4,x_6,x_2)$。此外，在预测部分之前添加掩码 token $M_{z_{>c}}$，获得了一个新的输入token 序列 $(x_{z_{<=c}},M_{z_{>c}},x_{z_{>c}})=(x_1,x_3,x_5,[M],[M],[M],x_4,x_6,x_2)$和相应的位置序列 $(z_{<=c},z_{>c},z_{>c})=(p_1,p_3,p_5,p_4,p_6,p_2,p_4,p_6,p_2)$。在MPNet中，$(x_{z_{<=c}},M_{z_{>c}})=(x_1,x_3,x_5,[M],[M],[M])$为非预测的部分，$x_{z_{>c}}=(x_4,x_6,x_2)$ 为预测的部分。对于非预测部分$(x_{z_{<=c}},M_{z_{>c}})$，采用双向建模来提取表示，在上图（a）中用灰色的线来表示。

Modeling Output Dependency with Two-Stream Self-Attention

对于被预测的部分$x_{z_{>c}}$，由于token 是排列顺序的，下一个被预测的标记可能出现在任何位置，这使得正常的自回归预测很困难。为此，使用PLM并采用双流自注意来自回归的预测token，如下图所示。

在双流自注意中，查询流（query stream）只能看到前面的token和位置以及当前的位置，不能看到当前的token，而内容流（content stream）可以看到前面和当前所有的token和位置。PLM中双流自注意的一个缺点是，在自回归预训练时，它只能看到排列序列中前面的token，而不知道整句话的位置信息，这就带来了预训练和微调之间的差异。为了解决这个限制，修改了位置补偿。

Reducing Input Inconsistency with Position Compensation

为了确保模型能够看到完整的句子，提出了位置补偿，这使下游任务更加一致。通过仔细设计查询和内容流的注意掩码，以确保每个步骤总是可以看到n个token，其中n是原始序列的长度(在上面的例子中，n = 6)。

例如，在预测token $x_{z_5}=x_6$时，原双流注意中的查询流将掩码token $M_{z_5}=[M]$和位置 $p_{z_5}=p_6$作为注意查询，在内容流中只能看到前面的token $x_{z_{<5}}=(x_1,x_3,x_5,x_4)$和位置 $p_{z_{<5}}=(p_1,p_3,p_5,p_4)$，而不能看到位置$p_{z_{>=5}}=(p_6,p_2)$，从而错失完整的句子信息。根据位置补偿，上图（b）中最后的两行，查询流可以看到额外的token $M_{z_{>=5}}=([M],[M])$和位置$p_{z_{>=5}}=(p_6,p_2)$，内容流中的位置补偿也类似。这样就可以大大减少预训练和微调之间的输入不一致。

模型参考

论文地址：https://arxiv.org/abs/2004.09297

代码地址：https://github.com/microsoft/MPNet