多目标关联算法-匈牙利匹配

1. 前言

  前面提到，传感器每帧数据检测出的Object通常不止一个，而如果要进行不同模态或者单传感器多帧检测结果之间的关联，势必会涉及到Object集合之间的匹配问题。如下图红色点和绿色点之间的匹配。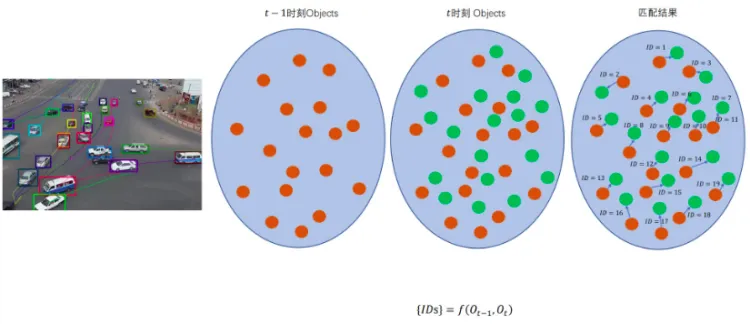

  一般而言，这种问题通常叫做二分图的最大匹配问题。而匈牙利算法(Hungarian Algorithm)和KM算法(Kuhn-Munkres Algorithm)是其中比较经典的求解方法。匈牙利算法起源于 1955 年 Kuhn 提出的匈牙利方法（Hungarian Method），1956 年 Merrill M. Flood 给出了匈牙利方法的算法实现步骤，1957 年 Munkres 针对该方法做了改进，后来大家习惯叫匈牙利算法或 Kuhn-Munkres 算法；
  匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法。该算法的核心是通过寻找增广路径来求二分图最大匹配的方法。最初的匈牙利算法中，每个匹配对象的地位被看做是相同的（即无权二分图），在这个基础上求取的最大匹配结果往往不是最优的。而在实际问题中，对象与对象之间的匹配度通常是存在差异的，如集合A中的a1可以和集合B中的{b1,b2,b3}进行匹配，但满意度方面 a1b1(0.8)>a1b2(0.6)>a1b3(0.3)。当我们不同对象的匹配关系加入权重概念之后，就演变成了带权二分图的最优匹配问题，KM算法则是主要用来解决此类问题的。目前人们常说的匈牙利算法和KM算法通常指的是同一个东西，都是用来求解带权二分图的最优匹配问题。

2. 基本概念

1. 图（Graph, G）：是由顶点集合（Vertices, V）和边集合（Edges, E）组成的二元组，表征了不同顶点间的拓扑链接关系。
   1. 根据图中的边是否具有单向性可将图分为有向图（Directed Graph）和无向图（Undirected Graph）；
   2. 根据图中的边是否具有不同的权重可将图分为有权图（Weighted Graph）和无权图（Unweighted Graph）。
2. 二分图（Bipartite Graph）：是一种特殊的图，也称二部图。二分图的顶点集可以被划分成两个互不相交的独立子集A和B，边集合内的每一条边的两个端点都分属于两个子集，但各子集内部的顶点互不相连。如下图，
   1. 二分图的判断可以通过染色法来实现，即图中所有所有顶点能否被染色成两类颜色，注意需要保证相连顶点不能同色。

3. 匹配（Matching）：给定图（G=(V, E)），它的一个匹配M表示联通两个子集的一条边，即包含于边集合E中的一个子集。注意匹配中的任意两条边之间没有公共顶点。如上图中的 a4-b3 和 a5-b2。
   1. 匹配 M 中的边称为匹配边，如上图中的两条红色边；匹配边的端点称为匹配点，如{a4, a5, b2, b3}；
   2. 边集合 E 中不属于匹配 M 的边称为未匹配边，如上图中其他的黑色边；顶点集合 V 中除匹配点外的顶点称为未匹配点，如{a1, a2, a3, b1, b4}。
4. 最大匹配（Maximum-Cardinality Matching）：表示图的所有匹配中边数最多的那些匹配（可能不唯一）。
5. 交替路（Alternating Path）：给定图 G=(V,E) 和它的一个匹配 M，交替路（Alternating Path）描述的是图中的这样一条路径：从图中的某个未匹配点出发，交替经过未匹配边和匹配边形成的路径。
6. 增广路（Augmenting Path）：是一条特殊的交替路，增广路是从图中的某个未匹配点出发，交替经过未匹配边和匹配边，并终止于另一未匹配点的路径。即起终点均是未匹配点的交替路。
   

3. 指派问题-匈牙利算法原理

  网上关于原始匈牙利算法的介绍文档有很多，这里不再赘述。关于经典匈牙利算法的数学模型及处理流程可以参考B站视频：

• 第2.4讲-指派问题与匈牙利算法(上）_哔哩哔哩_bilibili
• 第2.4讲-指派问题与匈牙利算法(中)_哔哩哔哩_bilibili
• 第2.4讲-指派问题与匈牙利算法(下)_哔哩哔哩_bilibili
  

3.1 指派问题的数学模型

  假设有n项不同的工作或任务，需要n个人去完成，要求每人只完成一项工作，由于每人的知识、能力、经验的不同，各自完成不同任务所需要的时间也不同，问应该指派何人完成何项工作，使完成n项工作的总耗时最少?
$$min(z)=\sum _{i=1}^n\sum _{j=1}^n{C}_{ij}{X}_{ij}$$

• $X_{ij}$表示第 i 个人去完成第 j 份工作；
• $C_{ij}$为价值系数矩阵；

  将指派问题数学模型中效率系数 $c_{ij}$排成一个 n x n 矩阵，称为效率矩阵或价值系数矩阵，即$$C=\left[\begin{array}{cccc}{c}_{11}& c_{12}& ...& c_{1n}\\ c_{21}& c_{22}& ...& c_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ c_{n1}& c_{n2}& ...& c_{nn}\end{array}\right]$$

定理1

  设指派问题的效率矩阵为$C=(c_{ij}{)}_{n\ast n}$，若将该矩阵的某一行或某一列的各元素都减去同一个常数 t ，得到新的效率矩阵$C^{\prime }=(c_{ij}^{{}^{\prime }}{)}_{n\ast n}$，则以$C^{{}^{\prime }}$为效率矩阵的新指派问题与原指派问题的最优解相同，但其最优解比原最优解减少 t 。

定理2

  若将指派问题的效率矩阵每一行及每一列分别减去各行及各列的最小元素，则得到的新指派问题与原指派问题有相同的最优解。

4. 多目标关联-KM算法

  多传感器融合中的目标关联问题通常也被看做带权二分图的最优匹配问题。本节主要是对基于原始匈牙利算法改进后的KM算法进行介绍，学习该算法是如何解决多目标数据关联问题的。
原始的匈牙利算法中有一步是：如何用尽量少的线覆盖代价矩阵中所有的0元素？这在代码中是不易实现的，而1957 年 James Munkres 提出的KM(Kuhn–Munkres) 算法中引入了“标星 0（starred zeros）”和“标撇 0（primed zeros）”的概念以改进匈牙利算法原始流程中的划线法。在算法执行过程中会选择性地对代价矩阵中的 0 元素标记星号（*）或者撇号（’）来辅助搜素增广路，其中，标星的 0 元素位置表示增广路中的匹配边，标撇的 0 元素位置表示增光路中的未匹配边。
  需要注意的地方是：KM算法主要适用于代价矩阵为方阵的情况。而数据关联问题中的待关联数据数量不一定相同，即代价矩阵不一定是方阵，这时候通常要进行膨胀补齐操作。对于有权二分图最小权匹配问题，可以通过“膨胀补最大值”的方式来构建代价方阵；而对于有权二分图最大权匹配问题，可以通过“膨胀补0”的方式来构建代价方阵以确保在求解过程中不会被选中。

4.1 算法流程

  算法的主流程如上：经过如上步骤的操作，问题的求解过程可以表述成一个状态机。示例如下：

// 函数表示整个KM算法流程：
// 隐含输入信息：待匹配目标数量：行数r、列数c, 二维代价矩阵 edge_cost
// 辅助变量：0元素标记矩阵、行/列标记矩阵
// 返回值：目标间的匹配结果
std::vector<std::pair<unsigned, unsigned>> solve(){
      int step           = 1;
      unsigned saved_row = 0, saved_col = 0;
      while(step) {
         switch(step) {
         case 1:
            step = step1(); // => [2]  
            break;
         case 2:
            step = step2(); // => [0, 3]
            break;
         case 3:
            std::tie(step, saved_row, saved_col) = step3(); // => [3, 4, 5]
            break;
         case 4:
            step = step4(saved_row, saved_col); // => [2]
            break;
         case 5:
            step = step5(); // => [3]
            break;
         }
      }

      // Collate the results
      std::vector<std::pair<unsigned, unsigned>> out;
      out.reserve(side());
      for(auto r = 0u; r < original_rows(); ++r)
         for(auto c = 0u; c < original_cols(); ++c)
            if(M(r, c) == STAR) out.push_back({r, c});
      return out;    
}

4.2 数据实例：

  下面用两个例子来描述一下KM算法的计算流程：

4.2.1 例子1：

  假设我们现在有一个 4x3 的量测代价矩阵（代价值是通过欧式距离等方式计算目标间距离得到），即航迹目标量有4个，传感器观测量3个，那么KM算法是如何匹配的呢？
量测代价矩阵
  现在我们将前面提到的KM算法流程应用到该代价矩阵上，计算满足其实现最小权的匹配结果。

  从上图可以看出，在第一步标星运算之后，标星元素能否覆盖到所有的列，因此匹配结束，输出结果为{1-2、3-3、4-1}，其中track_2匹配的是膨胀元素，无实际匹配值。

4.2.2 例子2：

  这里用ShiPeng博客中提到的数据为例，描述KM算法工作流程。
假设我们的航迹量测代价矩阵是个 4X3 的非方阵（4 个航迹 3 个量测，可能是传感器出现了漏检）。

  算法的工作流程如下：

  从上图可以看出，在第一步标星运算之后，标星元素能否覆盖到所有的列，因此匹配结束，输出结果为{2-2、3-3、4-1}，其中track_1匹配的是膨胀元素，无实际匹配值。

4.3 代码实现：

  这里只是截取了一部分的关键代码片段作为演示用途。

4.3.1 定义基础变量

enum MunkresState : uint8_t { NONE, STAR, PRIME };
using edge = std::pair<unsigned, unsigned>;

unsigned n_rows_ = 0;
unsigned n_cols_ = 0;
unsigned side_   = 0;
std::vector<T> data;
std::vector<MunkresState> marks;
std::vector<bool> row_mask;
std::vector<bool> col_mask;

// ------------------------------------------------------------- Construction
//
MunkresData(const unsigned n_rows,
           const unsigned n_cols,
           std::function<T(unsigned r, unsigned c)> edge_cost) noexcept
   : n_rows_(n_rows)
   , n_cols_(n_cols)
   , side_(std::max(n_rows, n_cols))
   , data(side_ * side_)
   , marks(side_ * side_)
   , row_mask(side_)
   , col_mask(side_){}

// ---------------------------------------------------------- Getters/Setters
//
// Costs
T& C(int r, int c) noexcept { return data[r * side_ + c]; }
const T& C(int r, int c) const noexcept { return data[r * side_ + c]; }

// Marks
MunkresState& M(int r, int c) noexcept { return marks[r * side_ + c]; }
const MunkresState& M(int r, int c) const noexcept { return marks[r * side_ + c]; }

void cover_row(int r) noexcept { row_mask[r] = true; }
void cover_col(int c) noexcept { col_mask[c] = true; }
void uncover_row(int r) noexcept { row_mask[r] = false; }
void uncover_col(int c) noexcept { col_mask[c] = false; }
bool is_row_covered(int r) const noexcept { return row_mask[r]; }
bool is_col_covered(int c) const noexcept { return col_mask[c]; }

unsigned original_cols() const noexcept { return n_cols_; }
unsigned original_rows() const noexcept { return n_rows_; }
unsigned side() const noexcept { return side_; }

4.3.2 初始化

void init(){   // Populate weight matrix... keep track of maximum for next step
  T max_val = std::numeric_limits<T>::lowest();
  for(auto r = 0u; r < n_rows; ++r)
     for(auto c = 0u; c < n_cols; ++c) {
        auto val = edge_cost(r, c);
        C(r, c)  = val;
        if(max_val < val) max_val = val;
     }

  // The weight matrix is always square... fill in the empty
  // spots with 'max-val'
  for(auto r = n_rows; r < side(); ++r)
     for(auto c = n_cols; c < side(); ++c) C(r, c) = max_val;
  for(auto c = n_cols; c < side(); ++c)
     for(auto r = n_rows; r < side(); ++r) C(r, c) = max_val;

  // Subtract the minimum from every row and column, which
  // ensures that every row and column has a '0'
  subtract_min_from_all_rows_cols();

  // Set up marks
  std::fill(begin(marks), end(marks), MunkresState::NONE);
  std::fill(begin(row_mask), end(row_mask), false);
  std::fill(begin(col_mask), end(col_mask), false);    
}

// ------------------------------------------ subtract min from all rows cols
// This prepares the data for the algorithm
void subtract_min_from_all_rows_cols()
{
  auto min_val_in_row = [&](unsigned r) -> T {
     auto min_val = C(r, 0);
     for(auto c = 1u; c < side_; ++c)
        if(C(r, c) < min_val) min_val = C(r, c);
     return min_val;
  };

  auto min_val_in_col = [&](unsigned c) -> T {
     auto min_val = C(0, c);
     for(auto r = 1u; r < side_; ++r)
        if(C(r, c) < min_val) min_val = C(r, c);
     return min_val;
  };

  // Minimize each row
  for(auto r = 0u; r < side_; ++r) {
     const auto min_val = min_val_in_row(r);
     for(auto c = 0u; c < side_; ++c) C(r, c) -= min_val;
  }

  // Minimize each col
  for(auto c = 0u; c < side_; ++c) {
     const auto min_val = min_val_in_col(c);
     for(auto r = 0u; r < side_; ++r) C(r, c) -= min_val;
  }
}

4.3.3 Step-1

// ------------------------------------------------------------------- Step 1
// Iterate over each element...
// If it's 0, and there's no other zero in row/col, then STAR
int step1() noexcept
{
  std::vector<bool> r_mask(side(), false);
  std::vector<bool> c_mask(side(), false);
  for(auto r = 0u; r < side(); ++r) {
     if(r_mask[r]) continue;
     for(auto c = 0u; c < side(); ++c) {
        if(r_mask[r] || c_mask[c]) continue;
        if(C(r, c) == zero) {
           M(r, c)   = STAR;
           r_mask[r] = true;
           c_mask[c] = true;
        }
     }
  }
  return 2;
}

4.3.4 Stpe-2

// ------------------------------------------------------------------- Step 2
// Cover each column containing a STAR
int step2() noexcept
{
  auto counter = 0u;

  for(auto c = 0u; c < side(); ++c) assert(!is_col_covered(c));

  for(auto r = 0u; r < side(); ++r) {
     for(auto c = 0u; c < side(); ++c) {
        if(is_col_covered(c)) continue;
        if(M(r, c) == STAR) {
           cover_col(c);
           counter++;
        }
     }
  }

  // A complete matching
  if(counter >= side()) return 0;

  return 3;
}

4.3.5 Step-3

// ------------------------------------------------------------------- Step 3
// Find a uncovered zero and PRIME it.
// Eventually get to a state where the PRIMEd row contains no STAR zeros
std::tuple<int, unsigned, unsigned> step3() noexcept
{
  auto find_uncovered_row_col = [&](unsigned& r, unsigned& c) -> bool {
     for(r = 0; r < side_; ++r)
        if(!is_row_covered(r))
           for(c = 0; c < side_; ++c)
              if(!is_col_covered(c))
                 if(C(r, c) == zero) return true;
     return false;
  };

  // Find an uncovered zero, and mark it PRIME
  unsigned saved_row = 0, saved_col = 0;
  if(find_uncovered_row_col(saved_row, saved_col))
     M(saved_row, saved_col) = PRIME;
  else
     return std::tuple<int, unsigned, unsigned>{5, saved_row, saved_col}; // all zeros covered

  // If there's a STAR in the PRIMEd row, then:
  for(auto c = 0u; c < side(); ++c) {
     if(M(saved_row, c) == STAR) {
        cover_row(saved_row);             // cover that row
        uncover_col(c);                   // uncover the column
        return std::tuple<int, unsigned, unsigned>{3, saved_row, saved_col}; // and repeat this step
     }
  }

  // There's no STAR in the PRIMEd row, onto "augmenting path"
  return std::tuple<int, unsigned, unsigned>{4, saved_row, saved_col};
}

4.3.6 Step-4

// ------------------------------------------------------------------- Step 4
// Augmenting path algorithm
int step4(const unsigned saved_row, const unsigned saved_col) noexcept
{
  auto find_star_in_col = [&](const unsigned c) -> int {
     for(auto r = 0u; r < side(); ++r)
        if(M(r, c) == STAR) return r;
     return -1; // row not found
  };

  auto find_prime_in_row = [&](const unsigned r) -> int {
     for(auto c = 0u; c < side(); ++c)
        if(M(r, c) == PRIME) return c;
     assert(false); // we should ALWAYS find this column
     return -1;     // col not found
  };

  auto make_path = [&](const edge e0) {
     std::vector<edge> seq;
     seq.reserve(side());
     seq.push_back(e0);
     int r = -1, c = -1;
     while(true) {
        c = seq.back().second;
        r = find_star_in_col(c); // STARed zero in column of PRIMEd back()
        if(r >= 0)
           seq.push_back({r, c}); // Push a STAR edge
        else                      // If it doesn't exist, then the path is done
           break;
        c = find_prime_in_row(r);
        seq.push_back({r, c}); // Push a PRIME edge
     }
     return seq;
  };

  auto augment_path = [&](const std::vector<edge>& seq) {
     // For all edges in sequence:
     //    1. Erase all STARs
     //    2. And convert all PRIMEs to STARs
     for(const auto& e : seq) {
        if(M(e.first, e.second) == STAR)
           M(e.first, e.second) = NONE;
        else if(M(e.first, e.second) == PRIME)
           M(e.first, e.second) = STAR;
     }
  };

  auto erase_primes = [&]() {
     for(auto r = 0u; r < side(); ++r)
        for(auto c = 0u; c < side(); ++c)
           if(M(r, c) == PRIME) M(r, c) = NONE;
  };

  auto clear_covers = [&]() {
     std::fill(begin(row_mask), end(row_mask), false);
     std::fill(begin(col_mask), end(col_mask), false);
  };

  const edge e0{saved_row, saved_col}; // Uncovered primed zero from step3
  auto seq = make_path(e0);
  augment_path(seq);
  erase_primes();
  clear_covers();

  return 2;
}

4.3.7 Step-5

// ------------------------------------------------------------------- Step 5
// Find the smallest uncovered value, and:
//   1. Add it to every covered row
//   2. Subtract it from every uncovered col
int step5() noexcept
{
  auto find_min_uncovered_value = [&]() {
     auto minval = std::numeric_limits<T>::max();
     for(auto r = 0u; r < side(); ++r) {
        if(is_row_covered(r)) continue;
        for(auto c = 0u; c < side(); c++) {
           if(is_col_covered(c)) continue;
           if(C(r, c) < minval) minval = C(r, c);
        }
     }
     return minval;
  };
  const auto minval = find_min_uncovered_value();

  for(auto r = 0u; r < side(); ++r) {
     for(auto c = 0u; c < side(); c++) {
        if(is_row_covered(r)) C(r, c) += minval;  // (1) add minval
        if(!is_col_covered(c)) C(r, c) -= minval; // (2) subtract minval
     }
  }

  return 3;
}

4.3.8 主流程

// -------------------------------------------------------------------- Solve
//
std::vector<edge> solve() noexcept
{
  // The Munkres Algorithm is described as a state machine
  int step           = 1;
  unsigned saved_row = 0, saved_col = 0;
  while(step) {
     switch(step) {
     case 1:
        step = step1(); // => [2]
        break;
     case 2:
        step = step2(); // => [0, 3]
        break;
     case 3:
        std::tie(step, saved_row, saved_col) = step3(); // => [3, 4, 5]
        break;
     case 4:
        step = step4(saved_row, saved_col); // => [2]
        break;
     case 5:
        step = step5(); // => [3]
        break;
     }
  }

  // Collate the results
  std::vector<edge> out;
  out.reserve(side());
  for(auto r = 0u; r < original_rows(); ++r)
     for(auto c = 0u; c < original_cols(); ++c)
        if(M(r, c) == STAR) out.push_back({r, c});
  return out;
}

5. 小结

  二分图最大分配问题求解的核心在与增广路的反复查找及取反，直到达到最大匹配数。同样的带权二分图匹配问题的核心也是在于增广路的探索及扩展，所不同的是增广路边的构建与扩展需要依赖最小权或者最大权所在的边进行。

参考资料：

1. 多目标跟踪数据关联之匈牙利算法
2. 第2.4讲-指派问题与匈牙利算法(上-中-下）_哔哩哔哩_bilibili
3. 带你入门多目标跟踪（三）匈牙利算法&KM算法
4. 深蓝学院-多传感器融合感知