深入浅出 KNN 算法：原理、超参数调节及鸢尾花分类案例详解

KNN

1、什么是KNN

k nearest neighbors 是一种基础且简单的机器学习算法，属于监督学习中的分类与回归方法。

k近邻算法

通过计算新样本与训练集中所有样本的距离，选择距离最近的K 个邻居，根据这些邻居的类别（分类问题）或数值（回归问题）来预测新样本的结果。

k表示个数

邻居是什么样性质，类别，影响你，之所以成为了邻居，必然共性。

2、KNN过程实现

邻居，距离比较近

问题，请问Xu这个点属于哪个类别呢？

• 三个类别：红色、绿色、蓝色
• 找Xu这个点的最近的5个邻居（5 == k，调大跳小）
• 从图中直观看到，4个最近邻居是红色，1个最近的邻居是绿色
• 人多力量大，投票决定，民主。4 > 1
• 对人而言，投票
• 对计算机而言，统计
• 0.8 > 0.2
• 从票数或者从概率上分类的话，得到这样的结论
• Xu属于红色的类别！
• KNN根据远近，进行类别划分的基本原理

3、距离度量

点A(1,2)，点B(4,6)，请问A和B之间的距离怎么计算

• 欧式距离
  $$distanc{e}_{AB}=\sqrt{(4-1{)}^2+(6-2{)}^2}=\sqrt{3^2+4^2}=5$$
• 点A(2,3,4)，点B(5,8,9):
  $$distanc{e}_{AB}=\sqrt{(5-2{)}^2+(8-3{)}^2+(9-4{)}^2}$$
• 点A(x1,x2,x3,x4,……xn)，B(y1,y2,y3,y4,……yn)：
  $$distanc{e}_{AB}=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$

上面这个公式就是欧几里得距离公式

KNN算法的理论基础就是：

• 欧式距离
• 根据距离远近，选择邻居
• 物以类聚人以群分
• 这个算法不难！

4、KNN算法缺陷

• k给多少比较好呢？
• 请问绿色的点划归到红色类别，还是蓝色的类别？
• 如果k = 3，找三个邻居，2个是红色，1个蓝色 投票，红色票数多，所以此时，绿色球划归到，红色的类别
• 如果k = 5，找五个邻居，3个是蓝色，2个红色 投票，蓝色票数多，所以此时，绿色球划归到，蓝色的类别

分歧，不一致，不稳定，给定的k值不同，结果可能会不同！

5、KNN总结

KNN算法怎么找到邻居的呢？

• 电脑而言，给了一堆数据
• 电脑，计算所有点的距离！
• 然后排序！
• 选择距离比较小的k个点！
• 穷举
• KNN算法，比较耗费时间，要求数据量不能太大，时间复杂度空间复杂度，比较大。
• KNN这个算法，比较简单，但是，很多情况下，比较实用的。

数据，都是存在规律，精确度要求不高，KNN这个算法，可以实现分类功能。

KNN超参数

• weights权重，话语权：uniform（权重相同）、distance（用户自定义的权重函数：可以传递一个自定义函数，该函数接受一个包含距离的数组，并返回一个权重数组。）
• p = 1、2
• metrics = minkowski
• p = 1 曼哈顿距离

这个距离表示远近方法

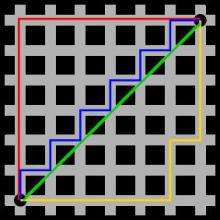
• 红色的线就是曼哈顿距离
• 蓝色和黄色等价曼哈顿距离
• 绿色线就是欧式距离
• p = 2 欧式距离

当 p = 1 时，计算的是曼哈顿距离（Manhattan distance），即 L1 范数。

当 p = 2 时，计算的是欧几里得距离（Euclidean distance），即 L2 范数。

一般来说，p 的默认值是 2，即使用欧几里得距离。如果需要使用其他的距离度量，可以根据需要调整 p 的值。

实例

def my_weight_function(distances):
    # 自定义逻辑，例如通过距离计算权重
    return 1 / (distances + 1e-5)
knn = KNeighborsClassifier(n_neighbors=5, weights=my_weight_function)

---

在代码中，weights='distance' 意味着使用距离加权方法，距离较近的邻居对分类结果的影响更大。这样可以使分类器更敏感于靠近测试样本的训练样本，从而可能提升分类性能。

不同的K值会导致不同的训练结果

import matplotlib.pyplot as plt 
from sklearn.neighbors import KNeighborsClassifier
knn=KNeighborsClassifier()
scores=[]
for k in range(2,50):
    knn.set_params(n_neighbors=k) #重新设置参数
    knn.fit(X_train,y_train)
    score=knn.score(X_test,y_test)
    scores.append(score)
plt.plot(np.arange(2,50),scores,'*r-')

---

KNN的案例

鸢尾花分类

• 生长的环境不同，所以类别3类
• 类别不同，性质不同：花萼长宽不一样，花瓣长宽不同了。
• 植物学家，根据形状不同，进行分类

分类算法使用流程：

• 加载数据
• 数据预处理，拆分
• 声明算法，给定超参数
• 训练算法，算法学习数据，归纳规律
• 算法，通过数学，找到，数据和目标值之间的规律
• 算法找到规律，应用
• 实际使用。

导包

#选择KNN分类算法
from sklearn.neighbors import KNeighborsClassifier
#导入鸢尾花数据集
from sklearn import datasets
#进行训练集测试集拆分
from sklearn.model_selection import train_test_split

---

加载数据

X,y=datasets.load_iris(return_X_y=True) 
#鸢尾花，分三类，鸢尾花花萼和花瓣长度
display(X,y)

---

#数据维度
#X必须是二维
#Y不做限定
display(X.shape,y.shape)

---

数据拆分

X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)
#从整个数据集进行拆分，测试集占20%（通常而言）
display(X_train.shape,X_test.shape)

---

算法建模

knn=KNeighborsClassifier(n_neighbors=5)  
#5个邻居，决定类别是哪一类
#数据规律，规律决定类别
#训练:建模、总结规律
knn.fit(X_train,y_train) 

---

算法验证

#使用测试集的数据对训练完成的模型测试
knn.predict(X_test) 

---

#测试集对应的真实数据
y_test

---

准确率

knn.score(X_test,y_test)

---

也可以用预测输出的值和真实值比较，正确的值占总数的比例即正确率

(y_test==knn.predict(X_test)).mean()

---

算法模型保存

import joblib 
#保存在当前目录下，取名为model
joblib.dump(knn,'./model')

---

模型调用

model=joblib.load('./model')

---

import numpy as np 
#随机给一个实验数据
X_new=np.array([[5.4,3.2,0.8,2.3]])
model.predict(X_new)  #判定属于鸢尾花类别为0

---

快去试试吧！