目录
正则化线性回归
在练习的前半部分,您将实现正则化线性回归,利用水库水位的变化来预测从大坝流出的水量。在下半部分中,您将对调试学习算法进行一些诊断,并检查偏差和偏差的影响。
数据可视化
首先,我们将可视化包含水位变化的历史记录的数据集,X和从大坝流出的水量y。这个数据集包括三个部分
训练集X,y,用于训练模型
验证集Xval,yval,用于选择正则化参数
测试集Xtest,ytest, 用于评估性能
首先我们需要先导入所用到的库
import numpy as np
import scipy.io as sio
import scipy.optimize as opt
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns接着导入本次实验中所用到的数据,在这里我们可以将数据集分别提出来,并查看其大小
# 读入数据
path = r'E:\Code\ML\ml_learning\ex5-bias vs variance\ex5data1.mat'
data = sio.loadmat(path)
X, y, Xval, yval, Xtest, ytest = data['X'], data['y'], data['Xval'], data['yval'], data['Xtest'], data['ytest']
# X.shape, y.shape, Xval.shape, yval.shape, Xtest.shape, ytest.shape
# ((12, 1), (12, 1), (21, 1), (21, 1), (21, 1), (21, 1))接下来进行数据可视化
# 可视化
def plotdata(X,y):
plt.figure(figsize=(12,8))
plt.scatter(X, y,c='r', marker='x')
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')
plt.grid(True)
plotdata(X,y)
正则化线性回归代价函数
正则化线性回归的代价函数如下
其中λ是控制正则化程度的正则化参数,因此可以用于防止过拟合,正则化项对总代价J(θ)施加惩罚,随着模型参数θj的增大,惩罚也增大,需要注意的是不惩罚θ0项,即索引从1开始
# 插入x0 = 1
X, Xval, Xtest = [np.insert(x, 0, np.ones(x.shape[0]), axis=1) for x in (X, Xval, Xtest)]
# X.shape, Xval.shape, Xtest.shape
# ((12, 2), (21, 2), (21, 2))
# 代价函数
def costReg(theta, X, y, l=1):
m = X.shape[0] # 12
theta = np.matrix(theta) # (1,2)
X = np.matrix(X) # (12,2)
y = np.matrix(y) # (12,1)
inner = (X * theta.T) - y # (12,1)
part1 = float((1 / (2 * m)) * inner.T * inner) #(1,1)
part2 = float((l / (2 * m)) * theta[:,1] * theta[:,1].T) # (1,1)
cost = part1 + part2
return cost其中当初始θ = [1;1]时,所得输出为303.993,在这里一定要注意公式后半部分正则化处不包括θ0这一项,不然输出就变成304.04,反复检查了好几遍才发现这里出了问题。
正则化线性回归梯度
相应地,正则化线性回归梯度公式定义为
# 正则化梯度下降
def gradientReg(theta, X,y, l=1):
m = X.shape[0] # 12
theta = np.matrix(theta) # (1,2)
X = np.matrix(X) # (12,2)
y = np.matrix(y) # (12,1)
# (2,12) * ((12,2) * (2,1)) - (12, 1)) = (2,1)
inner = (1 / m) * X.T * ((X * theta.T) - y)
reg = (l /m) * theta # (1,2)
reg[0,0] = 0 #第0项不正则化
return inner + reg.T # (2,1)
代码中需要注意的就是计算θ0的梯度不需要正则化
当λ = 1所算得初始梯度为[-15.303; 598.250]
拟合线性回归
在这部分中,我们将λ设为0, 因为目前模型参数较少,正则化不会起什么大的帮助,并调用scipy.optimize中的minimize函数计算参数最优解,并将拟合函数与原始数据画在一起
# 拟合线性回归
final_theta = opt.minimize(fun=costReg, x0=theta, args=(X, y, 0), method='TNC', jac=gradientReg, options={'disp': True}).xdef plotdata1(theta, X, y):
fig,ax = plt.subplots(figsize=(12,8))
plt.scatter(X[:,1], y, c='r', label="Training data")
plt.plot(X[:,1], X @ theta, c = 'b', label="Prediction")
ax.set_xlabel("water_level")
ax.set_ylabel("flow")
ax.legend()
plt.show()
plotdata1(final_theta, X, y)
最佳拟合直线告诉我们,由于数据具有非线性,模型与数据的拟合不是很好。虽然如图所示可视化最佳拟合是调试学习算法的一种可能方法,但可视化数据和模型并不总是那么容易。于是我们可以实现一个生成学习曲线的函数,即使数据不容易可视化,它也可以帮助调试学习算法。
偏差与方差
机器学习中的一个重要概念是偏差-方差权衡。偏差代表着模型与数据的拟合程度,高偏差的模型容易出现拟合不足,而方差代表着模型的泛化能力,高方差的模型对训练数据会出现过度拟合,即对新的样本泛化能力很差。我们可以通过绘制训练集与验证集的误差,来判断偏差与方差问题
学习曲线
为了绘制学习曲线,我们需要不同训练集大小的训练和交叉验证集误差。为了获得不同的训练集大小,你应该使用原始训练集X的不同子集。具体来说,对于一个训练集大小为i的集合,你应该使用前i个示例(即X(1:i,:)和y(1:i))。
模型的最优参数可以通过前面提到的minimize函数进行求解,得出模型参数后开始计算训练集与验证机上的误差,数据集的训练错误定义为
特别需要注意的是,训练误差不包括正则化项。计算训练误差的一种方法是使用您现有的代价函数并设置λ为0,只有当使用它来计算训练误差和交叉验证误差时。当计算训练集误差时,确保你是在训练子集(即X(1:n,:)和y(1:n))上计算它(而不是整个训练集)。但是,对于交叉验证错误,需要在整个交叉验证集上计算它。最后将计算的误差存储在向量、误差序列和误差值中,以便于可视化
# 学习曲线
def linear_regression(X,y,l=1):
"""求出最优参数"""
theta = np.ones(X.shape[1]) # 初始化参数
# 训练参数
res = opt.minimize(fun=costReg,x0=theta,args=(X,y,l),method='TNC',jac=gradientReg, options={'disp': True})
return res.x
def plot_learning_curve(X, y, Xval, yval, l):
"""画出学习曲线"""
m = X.shape[0]
training_cost, cv_cost = [], []
for i in range(1,m+1):
res = linear_regression(X[:i, :], y[:i], l)
tc = costReg(res, X[:i, :], y[:i], 0)
cv = costReg(res, Xval, yval, 0)
training_cost.append(tc)
cv_cost.append(cv)
plt.figure(figsize=(12,8))
plt.plot(np.arange(1, m+1), training_cost, label='training cost')
plt.plot(np.arange(1, m+1), cv_cost, label='cv cost')
plt.legend()
plt.xlabel("Number of training examples")
plt.ylabel("Error")
plt.title("Learing curve for linear regression")
plt.grid(True)
plt.show()
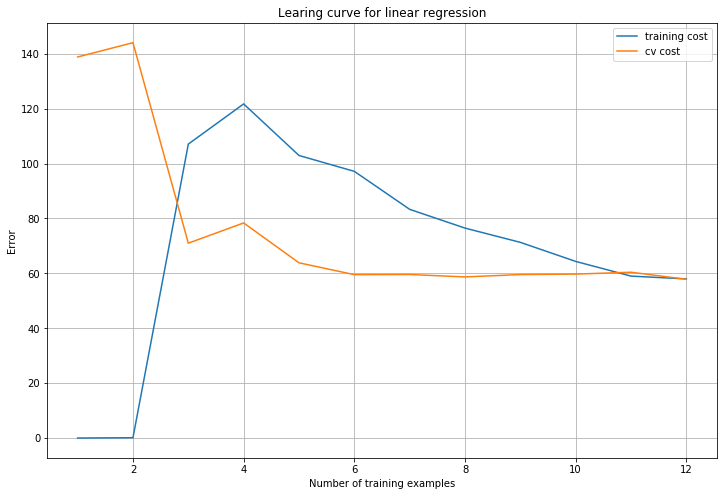
plot_learning_curve(X, y, Xval, yval, 0)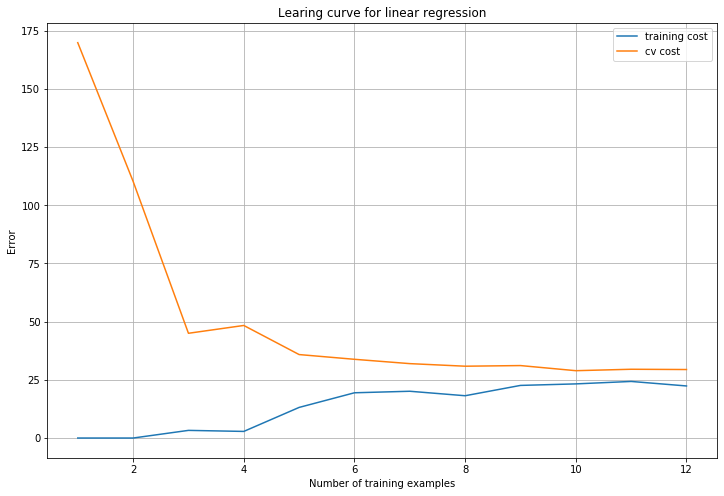
图中可知随着训练样本增加,两者误差都很高,说明线性回归不能很好拟合数据集,出现了高偏差问题。
多项式回归
在前面的模型中出现的问题是,它对数据过于简单,导致拟合很差,所以采用添加更多特征来解决此问题。对于多项式回归,假设形式如下,增加的特征为原始值的各种幂次。
def poly_features(X, power):
"""
多项式特征
每次在X最后一列添加次方项
从第二列开始插入,因为X本身含有一列x0 = 1
"""
Xpoly = X.copy()
for i in range(2, power + 1):
Xpoly = np.insert(Xpoly, Xpoly.shape[1], np.power(Xpoly[:,1], i), axis=1)
return Xpoly增加了特征之后,由于增加的特征为各次幂,故数据差异很大,比如x = 40,它的八次方就达到了10的12次方,所以我们需要对特征向量进行特征标准化。
def get_means_std(X):
"""获得训练集的均值和误差"""
means = np.mean(X,axis = 0) # 按列
# ddof = 1 求样本标准差
# ddof = 1 求总体标准差
stds = np.std(X, axis=0, ddof=1)
return means, stds
def featureNormalize(X, means, stds):
"""标准化"""
X_norm = X.copy()
X_norm[:,1:] = (X_norm[:,1:] - means[1:]) / stds[1:]
return X_norm在画学习曲线图之前我们需要进行数据预处理
# 数据处理
power = 6 # 扩展到x的6次方
# 均值与标准差
train_means, train_stds = get_means_std(poly_features(X, power))
# 标准化
X_norm = featureNormalize(poly_features(X, power), train_means, train_stds)
Xval_norm = featureNormalize(poly_features(Xval, power), train_means, train_stds)
Xtest_norm = featureNormalize(poly_features(Xtest, power), train_means, train_stds)接着画出学习曲线,这里画的是当λ = 0的情况
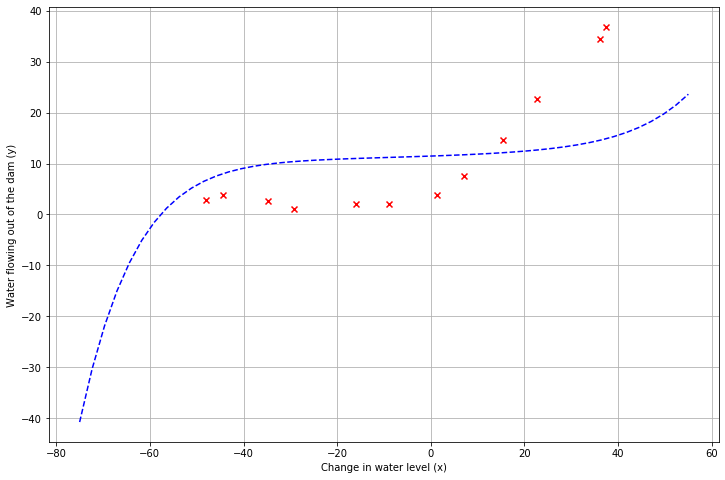
def plot_fit(means, stds, l):
"""画出拟合曲线"""
theta = linear_regression(X_norm,y, l)
x = np.linspace(-75,55,50)
xmat = x.reshape(-1, 1) # (50,)->(50,1)
xmat = np.insert(xmat,0,1,axis=1) # 添加x0 = 1
Xmat = poly_features(xmat, power) # 增加特征
Xmat_norm = featureNormalize(Xmat, means, stds) # 特征规范化
plotdata(X[:,1], y) # 画出原始数据
plt.plot(x, Xmat_norm @ theta, 'b--')# 画出拟合曲线
plot_fit(train_means, train_stds, 0)
plot_learning_curve(X_norm, y, Xval_norm, yval, 0) # 画出学习曲线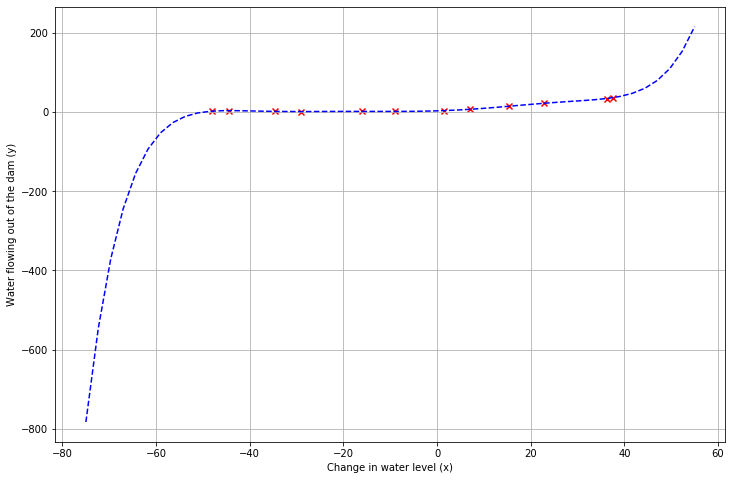
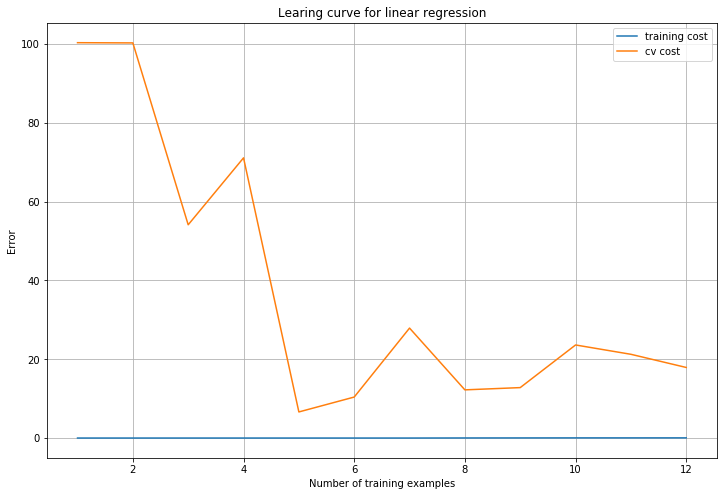
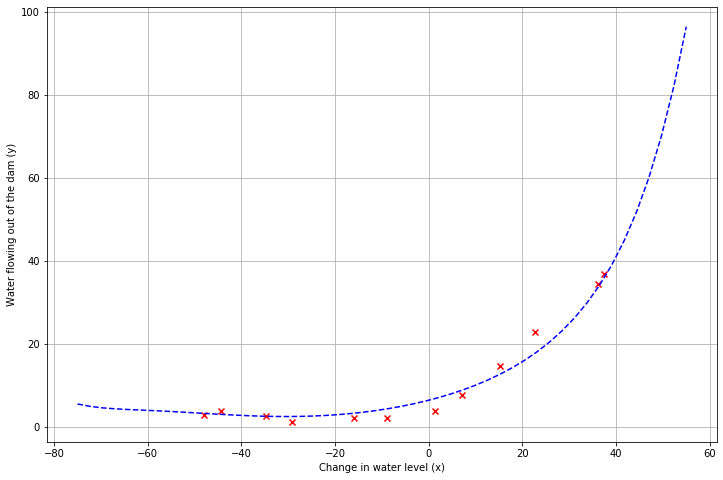
通过拟合图我们可以看得出多项式拟合能够很好跟随数据。通过学习曲线图可知,随着训练样本增加,训练误差比较低,虽然验证误差整体趋势是下降,但是最后的误差还是很大,训练误差与验证误差存在差距,说明模型对训练数据存在过拟合,高方差的问题,不能很好地推广。
而当λ = 1时,可以看出训练误差和验证误差都收敛到一个比较小的值,代表拟合程度还不错。

而当λ = 100 时,可以看出拟合效果很差,训练误差和验证误差都收敛到一个很大的值,说明正则化过多,模型无法拟合数据。
使用验证集选出λ
λ的取值可以选为[0., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1., 3., 10.]
lambdas = [0., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1., 3., 10.]
errors_train, errors_val = [], []
for l in lambdas:
theta = linear_regression(X_norm, y, l)
errors_train.append(costReg(theta,X_norm,y,0)) # 记得把lambda = 0
errors_val.append(costReg(theta,Xval_norm,yval,0))
plt.figure(figsize=(8,5))
plt.plot(lambdas,errors_train,label='Train')
plt.plot(lambdas,errors_val,label='Cross Validation')
plt.legend()
plt.xlabel('lambda')
plt.ylabel('Error')
plt.grid(True) 
lambdas[np.argmin(errors_val)] # 3.0可以得出验证误差最小的时候λ = 3
计算测试集错误
theta = linear_regression(X_norm, y, 3)
print('test cost(l={}) = {}'.format(3, costReg(theta, Xtest_norm, ytest, 0))
# test cost(l=3) = 4.407884454040075





















 1545
1545











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










