计算机软件实习项目三——迷宫

一、构建随机迷宫 应用不相交集合构建迷宫的算法简要描述如下：给定一个 N X N 的方格，初始时每个方格的四面都是墙（walls），如图所示，其中的 S 是迷宫的开始处，F 是迷宫的结束处。NN 迷宫的 N2 个方格 0，1，…，N2-1 初始时每个方格自己成为一个等价类，即{0}，{1}，…，{N2-1}。生成随机迷宫 的方法是随机选择一个内部墙（连接两个相邻方格的墙），如果该内部墙关联的 两个相邻的方格属于不同的等价类就将该墙除去，在除去该墙的同时将这两个等 价类合并。直到所有的方格都在一个等价类中，就完成了随机迷宫的生成构建随机迷宫 应用不相交集合。

二、迷宫求解

1.人为操作，通过接收键盘的输入信号实现上下左右的移动。

2.自动寻路：通过A*算法实现

A*算法：

.A*算法是一种常用的启发式搜索算法，被广泛应用于路径规划、游戏AI等领域。该算法基于最短路径优先原则，通过估计每个可能路径的代价，选择出最优解。在A*算法中，对每个节点进行评估和排序，并选择当前代价最小的节点进行扩展和探索。节点的代价由两部分组成：实际代价和启发式估价，即从起点到该节点的实际代价和从该节点到终点的估计代价之和。其中，启发式估价通常使用曼哈顿距离或欧几里得距离等方法进行计算。通过不断地扩展节点和更新代价，直到找到终点或遍历完所有节点。对于寻找路径较长或复杂的问题，A*算法可以在搜索过程中剪枝，减少搜索空间和提高效率。然而，A*算法可能存在局部最优解的问题，即搜索结果受到启发式估价的影响，容易被引导偏离全局最优解。为了解决这个问题，可以结合贪心最佳优先搜索和迭代加深搜索等方法进行改进。

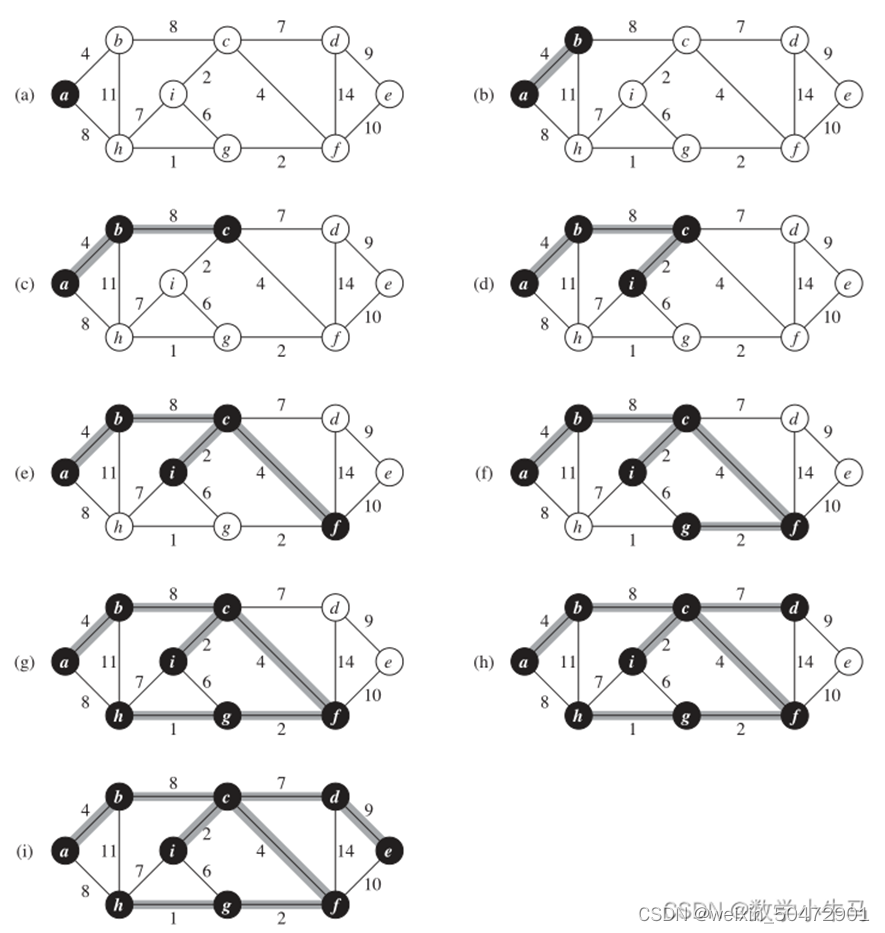
Dijkstra算法

Dijkstra算法是由计算机科学家Edsger W. Dijkstra在1956年提出的。

Dijkstra算法用来寻找图形中节点之间的最短路径。

考虑这样一种场景，在一些情况下，图形中相邻节点之间的移动代价并不相等。例如，游戏中的一幅图，既有平地也有山脉，那么游戏中的角色在平地和山脉中移动的速度通常是不相等的。

在Dijkstra算法中，需要计算每一个节点距离起点的总移动代价。同时，还需要一个优先队列结构。对于所有待遍历的节点，放入优先队列中会按照代价进行排序。

在算法运行的过程中，每次都从优先队列中选出代价最小的作为下一个遍历的节点。直到到达终点为止。

源码如下：

mainwindow.cpp:

#include "mainwindow.h"

#include "ui_mainwindow.h"

#define size 20

MainWindow::MainWindow(QWidget *parent) :

    QMainWindow(parent),

    ui(new Ui::MainWindow)

{
 

    ui->setupUi(this);

    int n = 31;

    m_maze = new Maze();

    m_maze->set_n(n);

    m_maze->mazeInit();

    m_maze->print();

    this->setW