信息论复习—率失真理论

目录

失真的概念：

信息率与失真的关系：

信息率失真理论：

失真函数矩阵：

平均失真度定义为：

平均失真度与信道转移概率的关系：

率失真函数：

率失真函数的物理意义：

 率失真函数的主要性质：

例：

汉明失真与传输差错概率：

汉明失真矩阵为 ：

由汉明失真矩阵，得平均失真度为：

而传输出错的概率：

---

理论上“消息完全无失真传送”的可实现性

        信道编码定理：无论何种信道，只要H(X)<=信息速率R<=信道容量C，总能找到一种编码，使在信道上能以任意小的错误概率和无限接近于C的传输速率来传送信息。反之，若R>C，则传输必失真。

实际上“消息完全无失真传送”的不可实现性

要做到无失真信源编码，要求H(X)<R<C；实际的信源常常是连续信源，连续信源的绝对熵无穷大,要无失真传送，则信息率R也需无限大，信道容量C也必须为无穷大。而实际信道带宽是有限的，所以信道容量受限制。因此无法满足无失真传输的条件，因此传输质量必然受影响。

实际生活中，人们一般并不要求获得完全无失真的消息，通常只要求近似地再现原始消息，即允许一定的失真存在。

失真的概念：

失真函数的取值通常反映失真产生的代价

---

信息率与失真的关系：

信源压缩后相比原始信源，误差或失真越大，说明压缩掉的信息量就越多。

      描述失真度大小和信息速率关系的定理称为：保真度准则下的信源编码定理，也叫信息率失真理论。

信息率失真理论的应用：

    信息率失真理论是量化、数模转换、频带压缩和数据压缩的理论基础

---

信息率失真理论：

失真函数矩阵：

与转移概率矩阵对应，可定义相应的失真度矩阵：

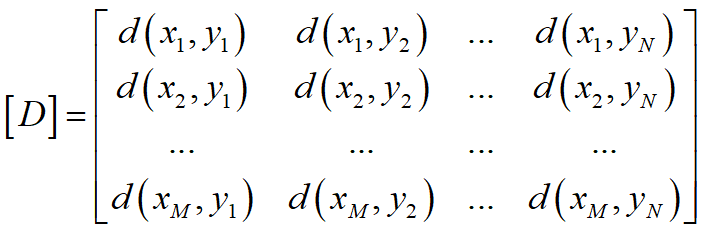
平均失真度定义为：

平均失真度是从统计意义上来说每个符号失真的平均值。

在通信传输系统中，失真通常在信道中产生，平均失真度与信道的关系可由转移概率的函数来描述。

平均失真度与信道转移概率的关系：

---

率失真函数：

      定义：给定信源和失真函数，要使信源压缩后的平均失真   (D为给定的失真上限)，则需找到某种压缩方法，使其经过压缩后可以达到一个允许的最小信息速率，即R(D)。不妨将该压缩过程假设成让信源通过一个有失真的传输信道（满足一定的信道转移概率分布或转移概率密度函数），使在该信道（称为试验信道）上传输的信息速率达到最小，这个最小的信息速率称为信息率失真函数，记作R(D)。

率失真函数示意图：

 

率失真函数的物理意义：

如果将符号通过信道传输看作某种变换过程，为了以小于等于DC 的失真度恢复信源的输出，平均每个信源符号需要得到的最小信息量。

若将率失真函数看作D的函数，显然有如下的关系：

当没有失真时( D=0   ):

当失真达到最大时( D=Dmax   )：

率失真函数的定义域：

 率失真函数的主要性质：

(1))率失真函数R(D)是D的下凸型凸函数。 作为D的函数存在最小值。

(2)率失真函数R(D)是D的单调递减函数。允许的失真越大，所需的互信息量越小。   

(3))R(D)是D的连续函数。

例：

---

汉明失真与传输差错概率：

设信源符号的分布特性为：  

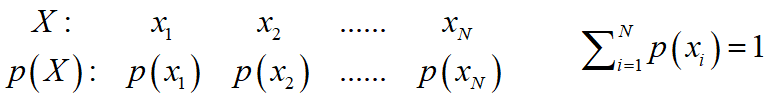
汉明失真矩阵为 ：

设信道转移矩阵为：

由汉明失真矩阵，得平均失真度为：

而传输出错的概率：

失真是由传输出错所致