支持向量机

最新推荐文章于 2024-09-01 11:39:17 发布

cpp_1211

最新推荐文章于 2024-09-01 11:39:17 发布

阅读量315

点赞数

文章标签：人工智能

本文链接：https://blog.csdn.net/weixin_51123341/article/details/128278539

版权

svm是最好的现成的分类器，不需要做任何修改即可实现。同时，这就意味着在数据上应用基本形式的svm分类器可以得到低错误率结果。svm能够对训练集之外的数据点做出很好的分类决策。

首先我们先来看看SVM做的是什么样的事，我们先看下面一张图

图中有三个分类实例，都将数据正确分类，我们直观上看，会觉得图中第三个效果会比较好，这是为什么呢？个人觉得人的直观感受更偏向于数据均匀对称的结构。当然，这只是直观感受，我们从专业的角度出发，第三种情况更优的原因在于它能容忍更多的数据噪声（tolerate more data noise），从而这个系统更加稳健（Robust），如下图所示，灰色的圈圈代表容忍噪声的大小门限，第三个门限最大，它比前面两个更优，而SVM就是寻求最大门限，构成分离数据正确且抗噪声强的稳健超平面（图中分类线是直线，一般数据维度是高维，对应的分类平面就是超平面）。

支持向量机
优点：泛化错误率低，计算开销不大，结果易解释。缺点：对参数调节和核函数的选择敏感，原始分类器不加修改仅适用于处理二类问题。适用数据类型：数值型和标称型数据

支持向量机

优点：泛化错误率低，计算开销不大，结果易解释。

缺点：对参数调节和核函数的选择敏感，原始分类器不加修改仅适用于处理二类问题。

适用数据类型：数值型和标称型数据

SVM算法的主要优点有：

    解决高维特征的分类回归问题很有效,在特征维度大于样本数时依然有很好的效果。
    仅仅使用一部分支持向量来做超平面的决策，无需依赖全部数据。
    使用核函数可以灵活的来解决各种非线性的分类回归问题。
    样本量不是海量数据的时候，分类准确率高，泛化能力强。

SVM算法的主要缺点有：

    特征维度远大于样本数时，SVM表现一般。
    SVM在样本量非常大，核函数映射维度非常高时，计算量过大，不太适合使用。
    非线性问题的核函数的选择没有通用标准，难以选择一个合适的核函数。
    SVM对缺失数据敏感。
    SVM要进行距离计算，需要对数据进行标准化处理，而决策树不需要。

一、基于最大间隔分隔数据

在二维空间上，两类点被一条直线完全分开叫做线性可分。如下图，在二维坐标下，样本空间中找到直线, 将不同类别的样本分开。

上述将数据集分隔开来的直线称为分隔超平面，即 $w^{T}x+b=0$ 。点 $x_i$ 位于红线之上都有 $wx_i+b>0$ ，而点 $x_j$ 位于红线之下有 $wx_i+b<0$ ，则两个区域是线性可分的。

寻找最佳的超平面

从二维扩展到多维空间中时，将 $D_0$ 和 $D_1$ 完全正确地划分开的 $w^{T}x+b=0$ 就成了一个超平面。为了使这个超平面更具鲁棒性，我们会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。我们希望找到离分隔超平面最近的点，确保它们离分隔面的距离尽可能远。这里点到分隔面的距离被称为间隔。我们需要的是间隔尽可能地大，这是因为如果犯错或者在有限数据上训练分类器的话，分类器尽可能健壮。支持向量就是离分隔超平面最近的那些点。

超平面方程： $w^{T}x+b=0$

二、寻找最大间隔

首先，我们来了解一下超平面：

分隔超平面的形式： $w^{T}x+b=0$ ，其中 $w = ( w _1 ; w_ 2 ; . . . ; w _n )$ ，当n = 2时，这就是在二维坐标上,其中为超平面的法向量，为偏置值。

从数学表示的层面上来看，实数域 $n$ 维空间中的超平面定义如下：

$w_1x_1+w_2x_2+......+w_nx_n=b$

超平面有以下几个性质：

性质1：法向量和偏置项以任意相同的倍数放缩，新表达式描述的仍然是原来的超平面。假设放缩比例为，令后得到的超平面表达式为，显然，这个表达式表示的仍然是原来的超平面。举个浅显的例子，直线 $2x_1+6x_2+8=4$ 与直线 $x_1+3x_2+4=2$ 是同一条直线，虽然他们的系数之比为2。

性质2：如下图，要计算点 X到分隔超平面的距离

就必须给出点到分隔面的法线或垂线的长度，点X到超平面的距离为：

其中 $\left \|w \right \|$ 表示的是，所有元素的平方和的开平方。

性质3：超平面将 $n$ 维空间划分为3部分，分为是：①点在超平面里；②点在超平面的“上方” ；③点在超平面的“下方”。如下图所示：需要注意的是，“上方”和“下方”并不是方位上的超平面上下方，而是以超平面的法向量 $w$ 的指向为准， $w$ 指向的方向称为“上方”，反之则为“下方”。

SVM中，分隔超平面是一个能够将正负样本恰好隔开的超平面，并且使得正样本在分隔超平面“上方”，负样本在分隔超平面”下方“。这就意味着 $w^{T}x+b=0$ ，分隔超平面中的 $w,b$ 需要满足以下条件：

其中为正样本点，为负样本点，而正负样本对应的标记值为，所以这两个条件可以改写成下面两个式子：

于是，对于线性可分的样本集：

，其中，，令，我们可以得到更加紧凑的表达："分类正确"

在SVM中，被称为样本点到超平面的函数间隔。

因此，我们可以得出结论，对于给定的线性可分的样本集合，必然存在分隔超平面可以将正负样本分开，该分类正确的超平面需要满足的条件为：样本点到超平面的函数间隔大于零。

在数学上，我们可以得到以下式子等效：

所以，为了方便后续的计算，简化方程为：

令 $X_+$ 和 $X_-$ 位于决策边界上，标签分别为正、负的两个样本，考虑 $X_+$ 到分类线的距离为:

$d_+=\frac{\left | w^Tx_++b \right |}{\left \| w \right \|}$

因此，分类间隔为：

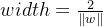
   $width = \frac{2}{\left \| w \right \|}$

最大化间隔也就是寻找参数 $w$ 和 $b$ , 使得 $width$ 最大，即：





通过数学知识可知，求 $\frac{2}{\left \| w \right \|}$ 的最大值，就是求 $\frac{\left \| w \right \|}{2}$ 的最小值，求最大值我们利用求导获取极值来解题，为了简化计算，因此问题可以等价于求 $\frac{\left \| w \right \|^2}{2}$ 的最小值：



到了这里，就得出了求解最大间隔超平面的最终表达式。

三、拉格朗日对偶问题

我们想要求解式得到最大间隔划分超平面对应的模型：

其中 $w,b$ 是模型参数，这里我们使用拉格朗日乘子法得到其对偶问题，从而高效的求出结果，下面就看一下什么是拉格朗日乘子法和对偶问题。

拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法，通过引入拉格朗日乘子，可将有d个变量与k个约束条件的优化问题转换为具有d+k个变量的无约束优化问题。

对偶问题：等式约束

给定一个目标函数 f : Rn→R，希望找到x∈Rn ，在满足约束条件g(x)=0的前提下，使得f(x)有最小值。该约束优化问题记为：

可建立拉格朗日函数：

其中 λ 称为拉格朗日乘数。因此，可将原本的约束优化问题转换成等价的无约束优化问题：

分别对待求解参数求偏导，可得：

一般联立方程组可以得到相应的解。

不等式约束的KKT条件

将约束等式 g(x)=0 推广为不等式 g(x)≤0。这个约束优化问题可改为：

同理，其拉格朗日函数为：

拉格朗日乘子法的几何意义即在等式g(x)=0或在不等式约束g(x)≤0下最小化目标函数f(x)，如下图：

①当 g(x)＜0 时：对f(x)求极值相当于闭区间求极值，最值点即为极值点，令λ=0，直接对f求梯度即可得到极值。

②当 g(x) = 0 时：说明极值点在边界取到，即g(x)＜0内的点值都大于边界，梯度的定义是向函数值增加最快的方向，所以f的梯度与g的梯度相反，从而存在常数λ＞0，使得：

其约束范围为不等式，因此可等价转化成Karush-Kuhn-Tucker (KKT)条件：

在此基础上，通过优化方式（如二次规划或SMO）求解其最优解。

四、SMO算法

SMO表示序列最小优化。这些小优化问题往往很容易求解，并且对它们进行顺序求解的结果与将它们作为整体来求解的结果是完全一致的。在结果完全相同的同时，SMO算法的求解时间短很多。 SMO算法的目标是求出一系列α和b，一旦求出了这些α，就很容易计算出权重向量w 并得到分隔超平面。

SMO算法的工作原理是：每次循环中选择两个α进行优化处理。一旦找到一对合适的α，那么就增大其中一个同时减小另一个。这里所谓的“合适”就是指两个α必须要符合一定的条件，条件之一就是这两个α必须要在间隔边界之外，而其第二个条件则是这两个α还没有进行过区间化处理或者不在边界上。

4.1 加载数据集


# 读取数据
def loadDataSet(fileName):
    dataMat = []  # 数据矩阵
    labelMat = []  # 数据标签
    fr = open(fileName)  # 打开文件
    for line in fr.readlines():  # 遍历，逐行读取
        lineArr = line.strip().split()  # 去除空格
        dataMat.append([float(lineArr[0]), float(lineArr[1])])  # 数据矩阵中添加数据
        labelMat.append(float(lineArr[2]))  # 数据标签中添加标签
    return dataMat, labelMat
# 绘制数据集
def showData():
    dataMat, labelMat = loadDataSet('tsetSetSvm.txt')         # 加载数据集，标签
    dataArr = array(dataMat)                               # 转换成numPy的数组
    n = shape(dataArr)[0]                                  # 获取数据总数
    xcord1 = []; ycord1 = []                               # 存放正样本
    xcord2 = []; ycord2 = []                               # 存放负样本
    for i in range(n):                                     # 依据数据集的标签来对数据进行分类
        if int(labelMat[i]) == 1:                          # 数据的标签为1，表示为正样本
            xcord1.append(dataArr[i, 0]); ycord1.append(dataArr[i, 1])
        else:                                              # 否则，若数据的标签不为1，表示为负样本
            xcord2.append(dataArr[i, 0]); ycord2.append(dataArr[i, 1])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=15, c='blue')             # 绘制正样本
    ax.scatter(xcord2, ycord2, s=15, c='red', marker='s')  # 绘制负样本
    plt.title('DateSet')                                   # 标题
    plt.xlabel('X1'); plt.ylabel('X2')                     # x，y轴的标签
    plt.show()

showData()

4.2 应用简化版 SMO 算法处理小规模数据集

from numpy import *
import matplotlib.pyplot as plt


# 读取数据
def loadDataSet(fileName):
    dataMat = []  # 数据矩阵
    labelMat = []  # 数据标签
    fr = open(fileName)  # 打开文件
    for line in fr.readlines():  # 遍历，逐行读取
        lineArr = line.strip().split()  # 去除空格
        dataMat.append([float(lineArr[0]), float(lineArr[1])])  # 数据矩阵中添加数据
        labelMat.append(float(lineArr[2]))  # 数据标签中添加标签
    return dataMat, labelMat


# 随机选择alpha
def selectJrand(i, m):
    j = i  # 选择一个不等于i的j
    while (j == i):  # 只要函数值不等于输入值i，函数就会进行随机选择
        j = int(random.uniform(0, m))
    return j


# 修剪alpha
def clipAlpha(aj, H, L):  # 用于调整大于H或小于L的alpha值
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj


# 简化版SMO算法
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = mat(dataMatIn)  # 数据矩阵dataMatIn转换为numpy的mat存储
    labelMat = mat(classLabels).transpose()  # 数据标签classLabels转换为numpy的mat存储
    b = 0;
    m, n = shape(dataMatrix)  # 初始化b参数，统计dataMatrix的维度m*n
    alphas = mat(zeros((m, 1)))  # 初始化alpha参数为0
    iter = 0  # 初始化迭代次数0
    while (iter < maxIter):  # matIter表示最多迭代次数，iter变量达到输入值maxIter时，函数结束运行并退出
        alphaPairsChanged = 0  # 变量alphaPairsChanged用于记录alpha是否已经进行优化
        for i in range(m):
            # 步骤1：计算误差Ei
            fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
            Ei = fXi - float(labelMat[i])
            # 优化alpha，同时设定容错率
            if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
                j = selectJrand(i, m)  # 随机选择另一个与alpha_i成对优化的alpha_j

                # 步骤1：计算误差Ej
                fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
                Ej = fXj - float(labelMat[j])

                # 保存更新前的aplpha值，使用拷贝
                alphaIold = alphas[i].copy();
                alphaJold = alphas[j].copy()

                # 步骤2：计算上下界L和H
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L == H:
                    print("L==H")
                    continue

                # 步骤3：计算eta
                eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - dataMatrix[
                                                                                                            j,
                                                                                                            :] * dataMatrix[
                                                                                                                 j, :].T
                if eta >= 0:
                    print("eta>=0")
                    continue

                # 步骤4：更新alpha_j
                alphas[j] -= labelMat[j] * (Ei - Ej) / eta

                # 步骤5：修剪alpha_j
                alphas[j] = clipAlpha(alphas[j], H, L)
                if (abs(alphas[j] - alphaJold) < 0.00001):
                    print("j not moving enough")
                    continue

                # 步骤6：更新alpha_i
                alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])  # 按与alpha_j相同的方法更新alpha_i

                # 步骤7：更新b_1和b_2，更新方向相反
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[
                    j] * (alphas[j] - alphaJold) * dataMatrix[i, :] * dataMatrix[j, :].T
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T - labelMat[
                    j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T

                # 步骤8：根据b_1和b_2更新b
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2) / 2.0

                # 统计优化次数
                alphaPairsChanged += 1
                print("第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))

        # 更新迭代次数
        if (alphaPairsChanged == 0):
            iter += 1
        else:
            iter = 0
        print("迭代次数: %d" % iter)
    return b, alphas
# 计算w值
def calcWs(alphas, dataArr, classLabels):
    X = mat(dataArr);
    labelMat = mat(classLabels).transpose()
    m, n = shape(X)
    w = zeros((n, 1))
    for i in range(m):
        w += multiply(alphas[i] * labelMat[i], X[i, :].T)
    return w


# 绘制数据集以及划分直线
def showDataLine(w, b):
    x, y = loadDataSet('tsetSetSvm.txt')
    xarr = array(x)
    n = shape(x)[0]
    x1 = [];
    y1 = []
    x2 = [];
    y2 = []
    for i in arange(n):
        if int(y[i]) == 1:
            x1.append(xarr[i, 0]);
            y1.append(xarr[i, 1])
        else:
            x2.append(xarr[i, 0]);
            y2.append(xarr[i, 1])

    plt.scatter(x1, y1, s=30, c='r', marker='s')
    plt.scatter(x2, y2, s=30, c='g')
    # 画出 SVM 分类直线
    xx = arange(0, 10, 0.1)
    # 由分类直线 weights[0] * xx + weights[1] * yy1 + b = 0 易得下式
    yy1 = (-w[0] * xx - b) / w[1]
    # 由分类直线 weights[0] * xx + weights[1] * yy2 + b + 1 = 0 易得下式
    yy2 = (-w[0] * xx - b - 1) / w[1]
    # 由分类直线 weights[0] * xx + weights[1] * yy3 + b - 1 = 0 易得下式
    yy3 = (-w[0] * xx - b + 1) / w[1]
    plt.plot(xx, yy1.T)
    plt.plot(xx, yy2.T)
    plt.plot(xx, yy3.T)
    # 画出支持向量点
    for i in range(n):
        if alphas[i] > 0.0:
            plt.scatter(xarr[i, 0], xarr[i, 1], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
    plt.xlim((-2, 12))
    plt.ylim((-8, 6))
    plt.show()

# 主函数
if __name__ == '__main__':
    dataMat, labelMat = loadDataSet('tsetSetSvm.txt')
    b, alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)
    w = calcWs(alphas, array(dataMat), labelMat)
    showDataLine(w, b)

4.3 利用完整Platt SMO算法加速优化

完整Platt SMO算法原理

Platt SMO算法是通过一个外循环来选择第一个alpha值的，并且其选择过程会在两种方式之间进行交替：一种方式是在所有数据集上进行单遍扫描，另一种方式则是在非边界alpha中实现单遍扫描。而所谓非边界alpha指的就是那些不等于边界0或C的alpha值。对整个数据集的扫描相当容易，而实现非边界alpha值的扫描时，首先需要建立这些alpha值的列表，然后再对这个表进行遍历。同时，该步骤会跳过那些已知的不会改变的alpha值。

在选择第一个alpha值后，算法会通过一个内循环来选择第二个alpha值。在优化过程中，会通过最大化步长的方式来获得第二个alpha值。在简化版SMO算法中，选择j之后计算错误率Ej。但在这里，则是建立一个全局的缓存用于保存误差值，并从中选择使得步长或者说 Ei-Ej最大的alpha值。


# 读取数据
def loadDataSet(fileName):
    dataMat = []  # 数据矩阵
    labelMat = []  # 数据标签
    fr = open(fileName)  # 打开文件
    for line in fr.readlines():  # 遍历，逐行读取
        lineArr = line.strip().split()  # 去除空格
        dataMat.append([float(lineArr[0]), float(lineArr[1])])  # 数据矩阵中添加数据
        labelMat.append(float(lineArr[2]))  # 数据标签中添加标签
    return dataMat, labelMat


# 随机选择alpha
def selectJrand(i, m):
    j = i  # 选择一个不等于i的j
    while (j == i):  # 只要函数值不等于输入值i，函数就会进行随机选择
        j = int(random.uniform(0, m))
    return j


# 修剪alpha
def clipAlpha(aj, H, L):  # 用于调整大于H或小于L的alpha值
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj
# 类
class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler, kTup):  # 使用参数初始化结构
        self.X = dataMatIn                                       # 数据矩阵
        self.labelMat = classLabels                              # 数据标签
        self.C = C                                               # 松弛变量
        self.tol = toler                                         # 容错率
        self.m = shape(dataMatIn)[0]                             # 数据矩阵行数m
        self.alphas = mat(zeros((self.m, 1)))                    # 根据矩阵行数初始化alpha参数为0
        self.b = 0                                               # 初始化b参数为0
        self.eCache = mat(zeros((self.m, 2)))                    # 第一列是有效标志
# 计算误差
def calcEk(oS, k):
    fXk = float(multiply(oS.alphas, oS.labelMat).T * (oS.X*oS.X[k,:].T)) + oS.b
    Ek = fXk - float(oS.labelMat[k])
    return Ek
# 内循环启发方式
def selectJ(i, oS, Ei):
    maxK = -1; maxDeltaE = 0; Ej = 0     # 初始化
    oS.eCache[i] = [1, Ei]               # 选择给出最大增量E的alpha
    validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:        # 循环使用有效的Ecache值并找到使delta E最大化的值
            if k == i: continue          # 如果k对于i，不计算i
            Ek = calcEk(oS, k)           # 计算Ek的值
            deltaE = abs(Ei - Ek)        # 计算|Ei-Ek|
            if (deltaE > maxDeltaE):     # 找到maxDeltaE
                maxK = k; maxDeltaE = deltaE; Ej = Ek
        return maxK, Ej
    else:                                # 在这种情况下（第一次），没有任何有效的eCache值
        j = selectJrand(i, oS.m)         # 随机选择alpha_j的索引值
        Ej = calcEk(oS, j)
    return j, Ej
#  计算Ek并更新误差缓存
def updateEk(oS, k):                     # 任何alpha更改后，更新缓存中的新值
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1, Ek]


# 优化的SMO算法
def innerL(i, oS):
    Ei = calcEk(oS, i)  # 计算误差Ei
    if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or (
            (oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
        # 使用内循环启发方式选择alpha_j并计算Ej
        j, Ej = selectJ(i, oS, Ei)
        # 保存更新前的aplpha值，拷贝
        alphaIold = oS.alphas[i].copy();
        alphaJold = oS.alphas[j].copy()

        # 步骤2：计算上下界L和H
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L == H: print("L==H"); return 0

        # 步骤3：计算eta
        eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T
        if eta >= 0: print("eta>=0"); return 0

        # 步骤4：更新alpha_j
        oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta

        # 步骤5：修剪alpha_j
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)

        # 更新Ej至误差缓存
        updateEk(oS, j)
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); return 0

        # 步骤6：更新alpha_i
        oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])

        # 更新Ei至误差缓存
        updateEk(oS, i)

        # 步骤7：更新b_1和b_2
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (
                    oS.alphas[j] - alphaJold) * oS.X[i, :] * oS.X[j, :].T
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (
                    oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T

        # 步骤8：根据b_1和b_2更新b
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
            oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
            oS.b = b2
        else:
            oS.b = (b1 + b2) / 2.0
        return 1
    else:
        return 0
# 完整的线性SMO算法
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(), C, toler, kTup)# 初始化
    iter = 0                                                                   # 初始化迭代次数为0
    entireSet = True; alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):       # 超过最大迭代次数或者遍历整个数据集都alpha也没有更新,则退出循环
        alphaPairsChanged = 0
        if entireSet:
            for i in range(oS.m):                                              # 遍历整个数据集
                alphaPairsChanged += innerL(i, oS)                             # 使用优化的SMO算法
                print("全样本遍历，第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))
            iter += 1
        else:                                                                  # 遍历非边界值
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]     # 遍历不在边界0和C的alpha
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                print("非边界遍历，第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))
            iter += 1
        if entireSet:
            entireSet = False                                                  # 切换整个集合循环
        elif (alphaPairsChanged == 0):
            entireSet = True
        print("迭代次数: %d" % iter)
    return oS.b, oS.alphas
# 计算w
def calcWs(alphas, dataArr, classLabels):
    X = mat(dataArr);
    labelMat = mat(classLabels).transpose()
    m, n = shape(X)
    w = zeros((n, 1))
    for i in range(m):
        w += multiply(alphas[i] * labelMat[i], X[i, :].T)
    return w


# 绘制数据集以及划分直线
def showData(w, b):
    x, y = loadDataSet('tsetSetSvm.txt')
    xarr = array(x)
    n = shape(x)[0]
    x1 = [];
    y1 = []
    x2 = [];
    y2 = []
    for i in arange(n):
        if int(y[i]) == 1:
            x1.append(xarr[i, 0]);
            y1.append(xarr[i, 1])
        else:
            x2.append(xarr[i, 0]);
            y2.append(xarr[i, 1])

    plt.scatter(x1, y1, s=30, c='r', marker='s')
    plt.scatter(x2, y2, s=30, c='g')

    # 画出 SVM 分类直线
    xx = arange(0, 10, 0.1)
    # 由分类直线 weights[0] * xx + weights[1] * yy1 + b = 0 易得下式
    yy1 = (-w[0] * xx - b) / w[1]
    # 由分类直线 weights[0] * xx + weights[1] * yy2 + b + 1 = 0 易得下式
    yy2 = (-w[0] * xx - b - 1) / w[1]
    # 由分类直线 weights[0] * xx + weights[1] * yy3 + b - 1 = 0 易得下式
    yy3 = (-w[0] * xx - b + 1) / w[1]
    plt.plot(xx, yy1.T)
    plt.plot(xx, yy2.T)
    plt.plot(xx, yy3.T)

    # 画出支持向量点
    for i in range(n):
        if alphas[i] > 0.0:
            plt.scatter(xarr[i, 0], xarr[i, 1], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')

    plt.xlim((-2, 12))
    plt.ylim((-8, 6))
    plt.show()
if __name__ == '__main__':
    dataMat, labelMat = loadDataSet('tsetSetSvm.txt')
    b, alphas = smoP(dataMat, labelMat, 0.6, 0.001, 40)
    w = calcWs(alphas, array(dataMat), labelMat)
    showData(w, b)