机器学习课程学习周报一

机器学习课程学习周报一

摘要

本周的学习内容主要围绕两方面，一个是李宏毅机器学习课程的第一章的学习，其中主要包括深度学习及术语的基本概念和线性模型。二是对docker容器化技术的基础学习，主要是了解docker的基本概念和简单命令。

Abstract

The main focus of this week’s study revolves around two aspects. Firstly, it involves studying the first chapter of Hung-yi Li’s machine learning course, which primarily covers the basic concepts of deep learning, including terminology and linear models. Secondly, it entails acquiring foundational knowledge about Docker containerization technology, primarily understanding the basic concepts of Docker and learning simple commands.

一、机器学习部分

1.1 机器学习概念

机器学习（Machine Learning）就是让机器具备找一个函数的能力，函数的输入和输出可以是多模态（Multimodal）的，输入可以是图片，文字，语音等，并从中提取特征（Feature），特征可以是向量（Vector），矩阵（Matrix）或序列（Sequence）。机器学习的目标是利用这些特征来训练模型，使其能够学习输入和输出之间的关系，从而预测新的、未见过的输入数据的输出。这个学习过程可以看作是在特征空间中寻找一个函数，该函数将输入映射到输出。机器学习解决的问题主要有以下几种：假设要找的函数的输出是一个数值，一个标量（Scalar），这种任务叫做回归（Regression）。另一个常见的任务是分类（Classification），人类先准备好一些类别（Class），现在的函数输出是设定好的选项中的一项。还有一种任务叫做结构化学习（Structured Learning），函数的输出是产生有结构的物体，比如让机器画一张图，写一篇文章等等。

图 机器学习中的不同输入与输出

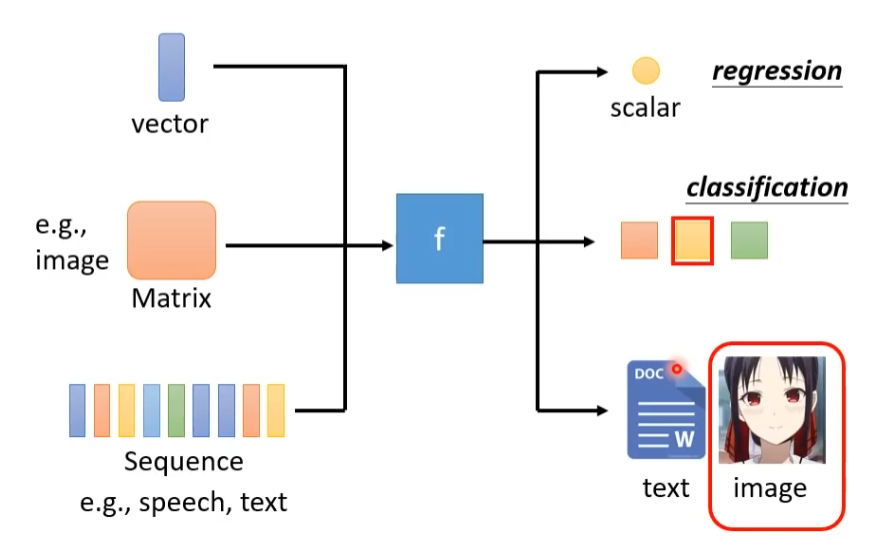
机器学习找函数的过程分为3个步骤：

第一个步骤是写出一个带有未知参数的函数$f$，例如将函数写成：
$$y=wx+b$$
带有未知参数的函数称为模型，$x$是输入的特征，$y$是输出的结果，$w$称为权重（Weight），$b$称为偏置（Bias）。

第二个步骤是定义损失$L$（Loss），损失也是一个函数。这个函数的输入是模型中的未知参数，即上述中的$w$和$b$，损失函数写成：
$$L=L(b,w)$$

现在我们有函数$f$的输出即为预测值$\hat{y}$以及真实值$y$，随后我们需要定义衡量预测值和真实值之间的**误差$e$（Error）**的方法，一般有：

• 平均绝对误差（Mean Absolute Error, MAE）

$$e=\left|\hat{y}-y\right|$$

• 均方误差（Mean Squared Error, MSE）

$$e={\left(\hat{y}-y\right)}^2$$

• 当$y$和$\hat{y}$都是概率分布时，使用交叉熵（Cross Entropy）

所以损失函数可以进一步写成：

$$L=L(b,w)=\frac{1}{N}\sum _n{e}_n$$
第三个步骤是解一个最优化的问题，找一组$w$和$b$使得损失$L$的值最小。我们用$w^{\ast }$和$b^{\ast }$代表最好的一组$w$和$b$，使得损失$L$的值最小，即：

$$w^{\ast },b^{\ast }=\underset{w,b}{\mathrm{argminL}}$$

而一般常用的优化算法为梯度下降法（Gradient descent），在阐述梯度下降法之前，需要先定义学习率$\eta$（Learning rate），$\eta$是一个超参数（hyperparameter），用以控制梯度下降中的步伐大小，下面介绍梯度下降法：

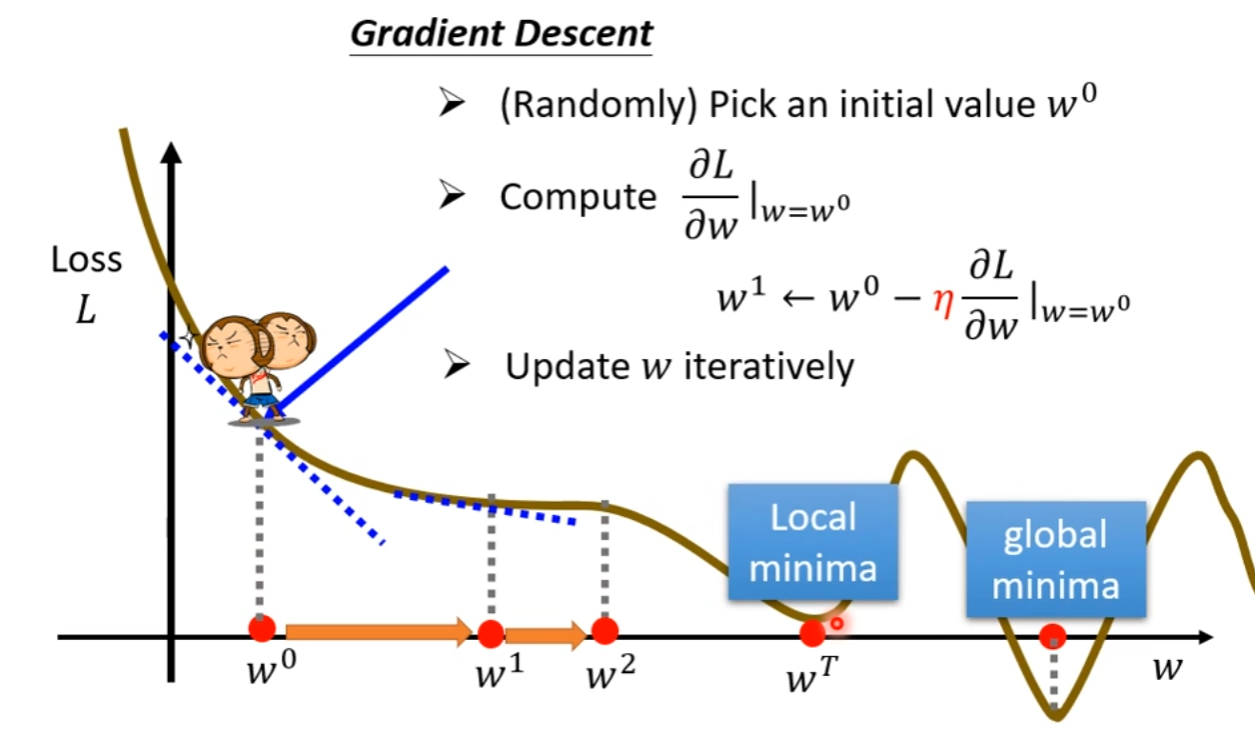
首先要随机选取一个初始点$w^0$，接下计算在$w=w^0$时，参数$w$对损失$L$的微分，即计算在$w^0$这个位置的的误差平面的切线斜率。然后用$w^0$减去这个微分乘上$\eta $的结果，则更新$w$到${w^1}$的新位置，即：

$$w^1=w^0-\eta {\frac{\partial L}{\partial w}|}_{w=w^0}$$

接下来计算$w^1$的微分，再计算移动到$w^2$，再反复做同样的操作，不断地移动$w$的位置，直到以下两种情况停下来：

• 当不断调整参数到一个地方时，它的微分值是0时，参数的位置就不再更新。
• 开始时会设定在调整参数时，计算微分的次数，当计算次数达到设定的上限时，就不再更新了，这也是个超参数。

梯度下降法的问题是：存在找到局部最小值，找不到全局最小值的问题。

图 梯度下降法

当把梯度下降法推广到两个参数时，即：
$$w^1=w^0-\eta {\frac{\partial L}{\partial w}|}_{w=w^0}$$

$$b^1=b^0-\eta {\frac{\partial L}{\partial b}|}_{b=b^0}$$

1.2 线性模型

这种把模型的输入特征$x$乘上一个权重，再加上一个偏置就得到结果$y$，这样的模型成为线性模型（Linear model）。但是线性模拟过于简单，无法拟合复杂的$y$和$x$的关系。

图 线性模型的局限性

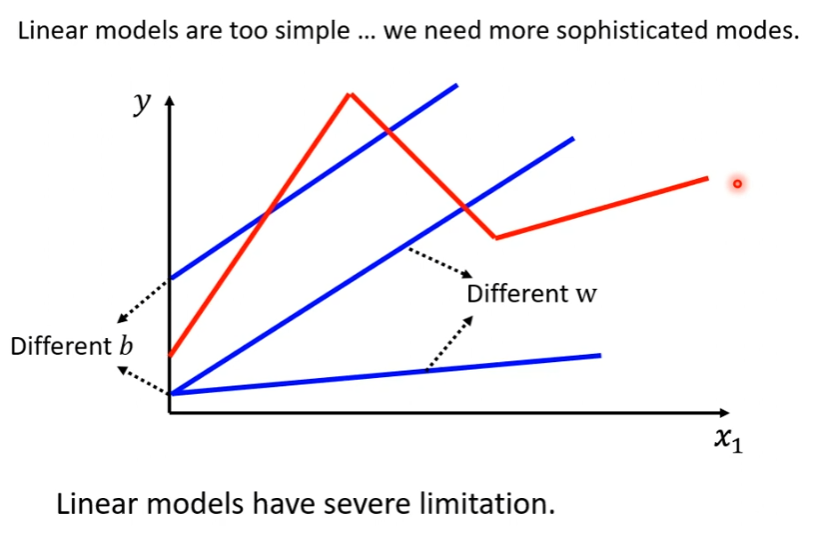
Hard Sigmoid函数的特性是当输入的$x$值，小于一个阈值时，$y$的值是一个定值；当输入的$x$值，大于另一个阈值时，$y$的值也是一个定值；在这两个阈值范围之内的$x$值，$y$值随着$x$值线性变化。为了拟合复杂的$y$和$x$的关系，我们用一个常数项加上一系列的Hard Sigmoid函数构成分段线性曲线（piecewise linear curve）。

图 分段线性曲线

当$y$和$x$的关系是一般曲线时，可以在这样的曲线上面，先取一些点，再把这些点连接起来，变成一个分段线性曲线模型。如果点取得足够多或点取的位置足够恰当，就可以用分段线性曲线逼近任意的连续曲线。

图 分段线性曲线拟合一般的曲线

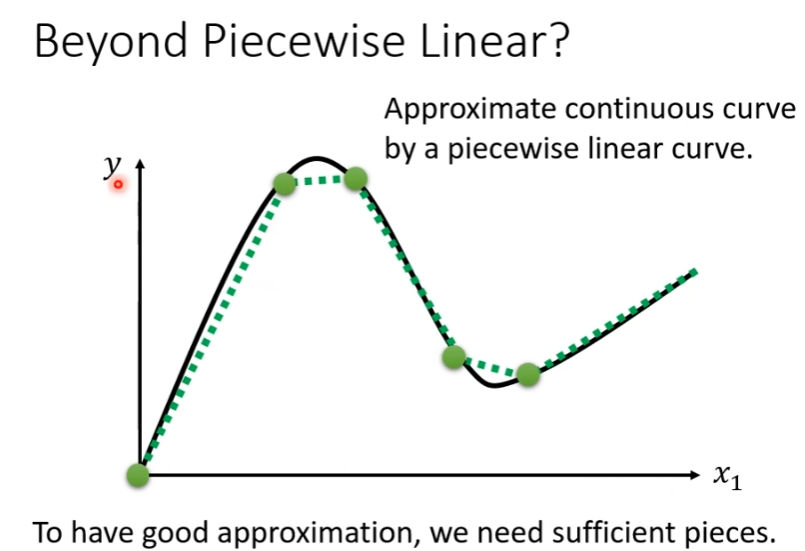
直接写Hard Sigmoid函数不是很容易，但是我们可以用Sigmoid函数来逼近Hard Sigmoid函数，Sigmoid函数的表达式为：
$$y=c\frac{1}{1+e^{-(b+w{x}_1)}}$$

图 Sigmoid函数逼近Hard Sigmoid函数

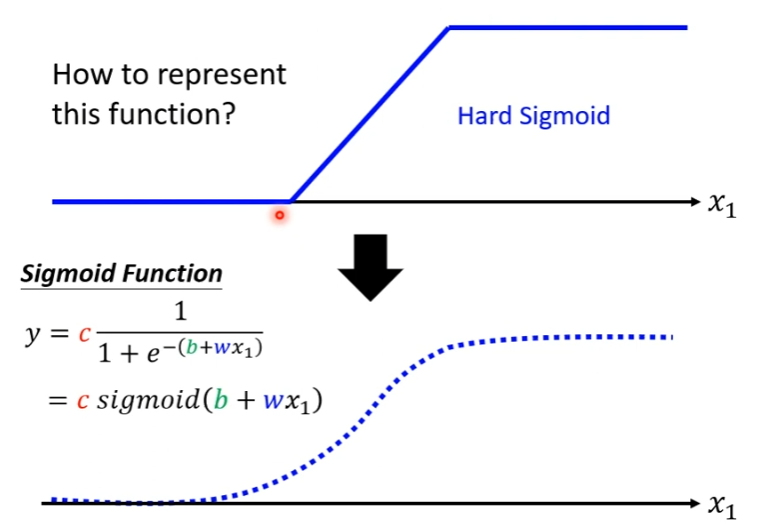
如果$x_1$的值，在趋于无穷大的时候，$e^{-(b+w{x}_1)}$这一项就会消失，当$x_1$非常大的时候，Sigmoid函数就会收敛在高度为$c$的地方。如果$x_1$负的非常大的时候，分母就会非常大，导致Sigmoid函数的值就会趋近于0，所以用Sigmoid函数来逼近Hard Sigmoid函数。同时Sigmoid函数还有另一种表达方式：

$$y=c\frac{1}{1+e^{-(b+w{x}_1)}}=c\sigma (b+w{x}_1)$$

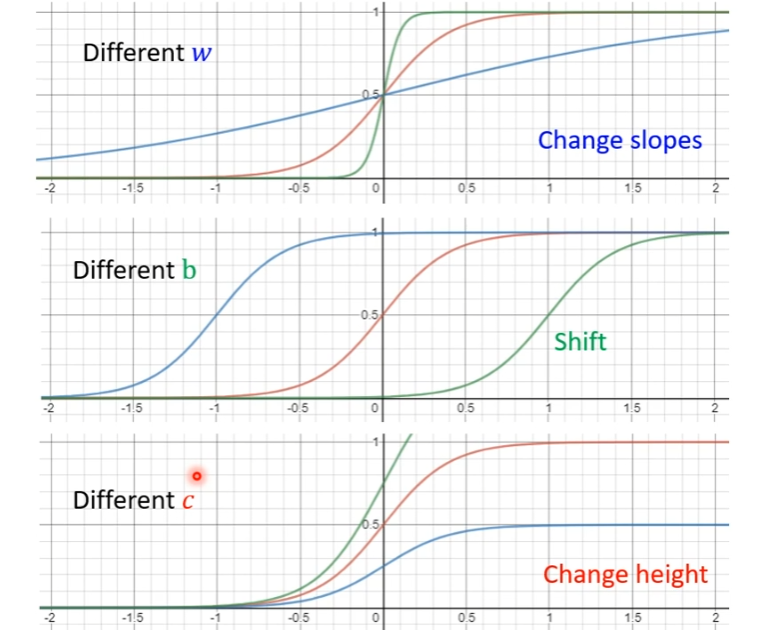
调整不同的$b$、$w$和$c$可以制造各种不同形状的Sigmoid函数，用不同形状的Sigmoid函数去逼近Hard Sigmoid函数：

图 不同b、w和c的Sigmoid函数

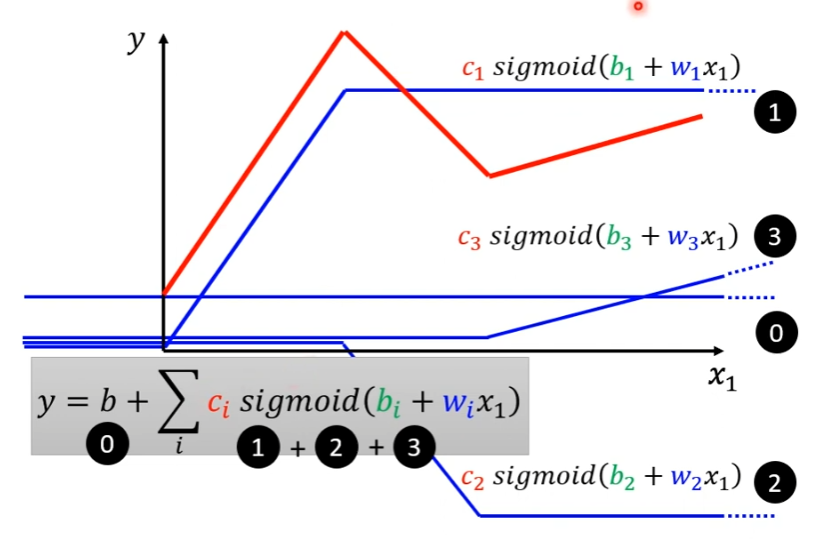
使用Sigmoid函数拟合$y$和$x$的复杂关系，即用一个常数项加上一系列Sigmoid函数，从下图来看，就是是常数项0、Sigmoid函数1、Sigmoid函数2以及Sigmoid函数3的和。

图 利用Sigmoid函数拟合y和x的复杂关系

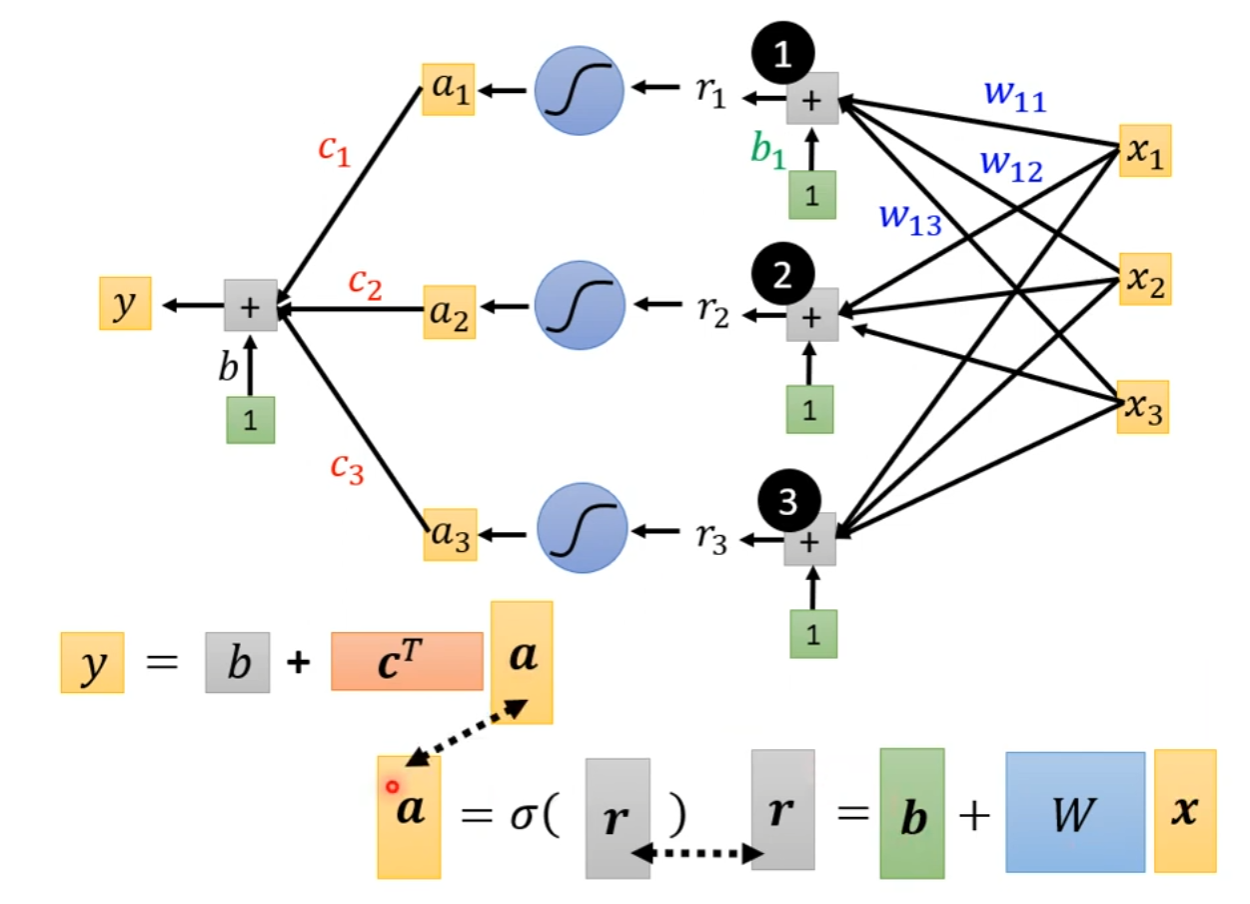
目前的特征只有单一的$x_1$，现在我们扩展到三个特征：$x_1$，$x_2$，$x_3$。每一个蓝色的分段线性函数都用一个Sigmoid函数来近似它。1,2,3 代表有3个 Sigmoid 函数。则单个的分段线性函数可以写成：

$$r_1=b_1+w_{11}{x}_1+w_{12}{x}_2+w_{13}{x}_3$$

其中$w_{ij}$代表在第$i$个Sigmoid函数里面，乘给第$j$个特征的权重，$$w$$的第一个下标$i$代表是现在考虑的是第一个 Sigmoid 函数，现在把3个函数都写出来：

$$r_1=b_1+w_{11}{x}_1+w_{12}{x}_2+w_{13}{x}_3$$

$$r_2=b_2+w_{21}{x}_1+w_{22}{x}_2+w_{23}{x}_3$$

$$r_3=b_3+w_{31}{x}_1+w_{32}{x}_2+w_{33}{x}_3$$

利用矩阵和向量相乘的方法，重新整理上述的等式：
$$\left[\begin{array}{c}{r}_1\\ r_2\\ r_3\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]+\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]$$
将其改成线性代数比较常用的表达方式为：
$$r=b+Wx$$

$r$对应的是$r_1$，$r_2$，$r_3$。$r_1$，$r_2$，$r_3$分别通过Sigmoid函数得到$a_1$，$a_2$，$a_3$，即：

$$a=\sigma (r)$$

因此，最后整个拟合$y$和$x$的关系的表达式应当写为：

$$y=b+c^{T}a$$

图 函数构建过程

图 函数的计算过程

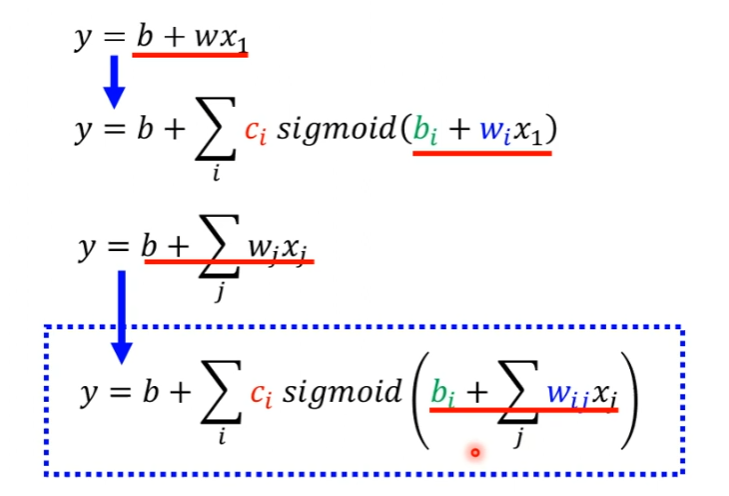
用$\theta$统设上述的所有参数$w$和$b$，则需要优化的参数可以表达为：

$$\theta =\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ {\theta }_3\\ ⋮\end{array}\right]$$
要找到$\theta$让损失越小越好，定义损失最小的一组$\theta$为${\theta }^{\ast }$，一开始要随机选一个初始的数值${\theta }^0$。接下来计算每一个未知的参数对$L$的微分，得到向量$g$，即：

$$g=\nabla L({\theta }^0)=\left[\begin{array}{c}{\frac{\partial L}{\partial {\theta }_1}|}_{\theta ={\theta }^0}\\ {\frac{\partial L}{\partial {\theta }_2}|}_{\theta ={\theta }^0}\\ ⋮\end{array}\right]$$

向量$g$称为梯度，$\nabla L$代表梯度。$L({\theta }^0)$是指梯度的位置，是在$\theta$等于${\theta }^0$的地方。计算出$g$后，接下来更新参数，${\theta }^0$代表它是一个随机的起始值，${\theta }^1$代表更新过一次的结果，以此类推更新参数的过程为：

$$\left[\begin{array}{c}{\theta }_1^1\\ {\theta }_2^1\\ ⋮\end{array}\right]\leftarrow \left[\begin{array}{c}{\theta }_1^0\\ {\theta }_2^0\\ ⋮\end{array}\right]-\left[\begin{array}{c}{\eta \frac{\partial L}{\partial {\theta }_1}|}_{\theta ={\theta }^0}\\ {\eta \frac{\partial L}{\partial {\theta }_2}|}_{\theta ={\theta }^0}\\ ⋮\end{array}\right]$$

实际中在使用梯度下降的时候，会把N笔数据随机分成一个一个的批量（Batch）。本来是把所有的数据拿出来算一个损失$L$，现在是只拿一个批量的数据算一个损失$L_1$，根据$L_1$算梯度，再用梯度来更新参数，接下来再选下一个批量算出损失$L_2$，根据$L_2$算梯度，再用梯度来更新参数。以此类推，将所有批量都计算过一次并更新过参数后，称为一个回合（epoch）。

1.3 模型变形

Hard Sigmoid函数还可以看作是两个 修正线性单元（Rectified Linear Unit, ReLU） 的加总，ReLU对应的公式为：

$$c\ast \max (0,b+w{x}_1)$$
ReLU函数的公式是指，比较0和$b+w{x}_1$的大小，结果会输出较大的那个。

图 使用ReLU表示Hard Sigmoid函数

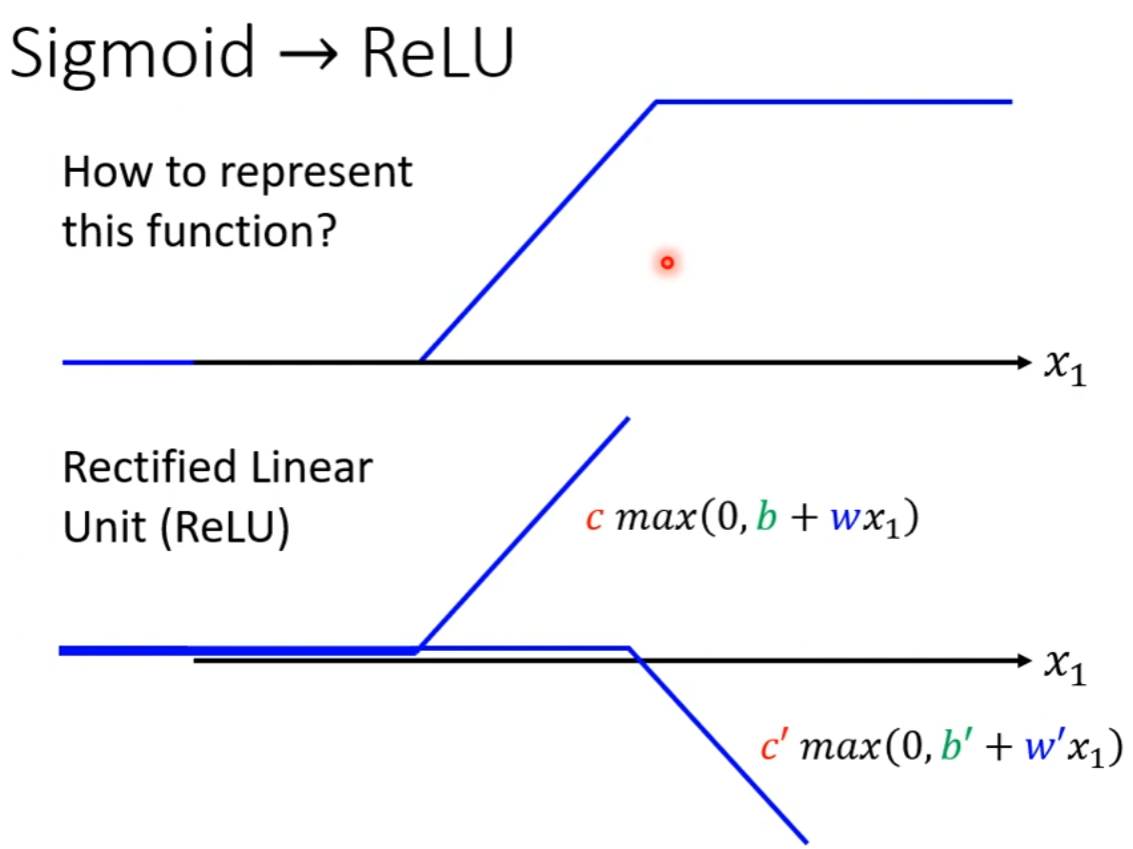
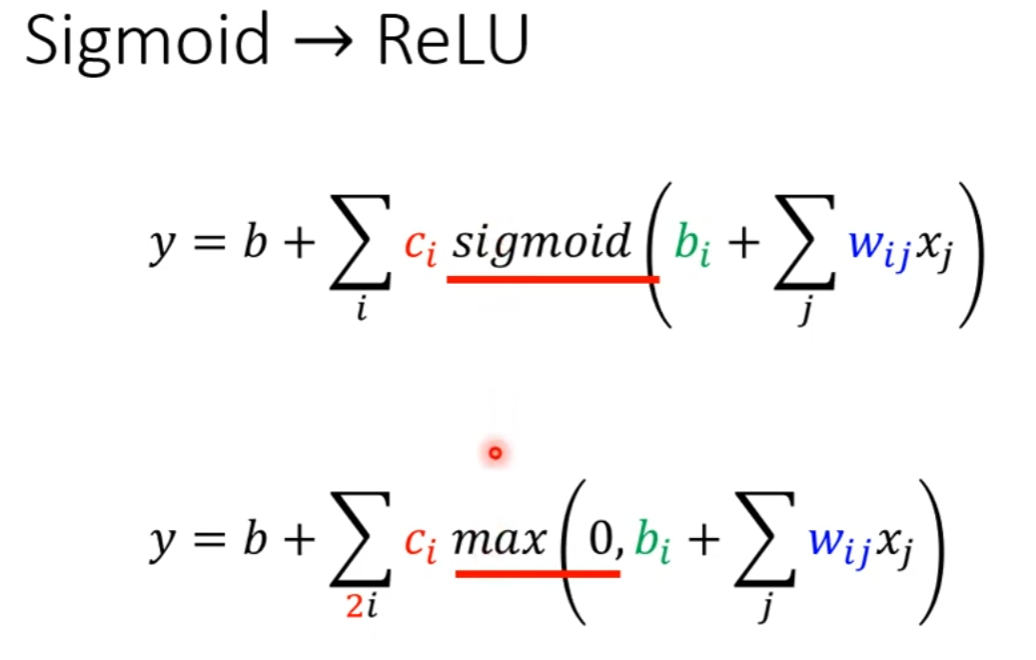
如上图所示，两个ReLU才能合成一个Hard Sigmoid。要合成i个Hard Sigmoid，需要i个Sigmoid，考虑ReLU时，则需要2i个ReLU。在机器学习里面，Sigmoid或ReLU称为激活函数（activation function）。

图 激活函数

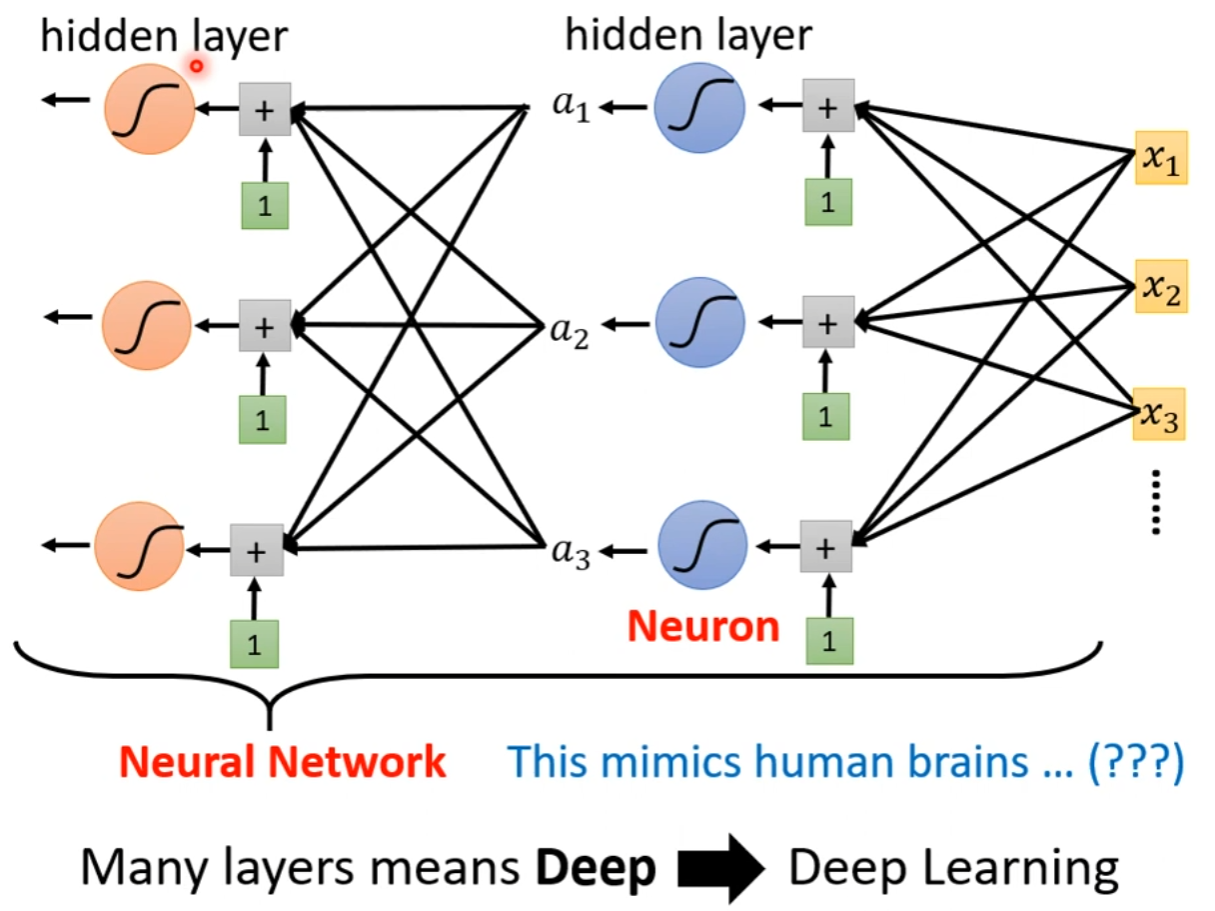
同时，Sigmoid或ReLU称为神经元（neuron），很多的神经元称为神经网络（neutral network）。人脑中就是有很多神经元，神经元串起来就是一个神经网络，因此神经网络就是就是在模仿人的大脑。每一排神经元又被称为一层，称为隐藏层（hidden layer）。

图 神经网络

二、docker学习部分

2.1 docker的基本组成

镜像（image）：

docker的镜像就好比是一个模板，可以通过这个模板来创建容器服务，一个镜像可以创建多个容器，最终服务或项目的运行就是在容器中的。

容器（container）:

docker利用容器技术，可以独立运行一个或一个组的应用，通过镜像来创建。包含启动，停止，删除等基本命令。

仓库（repository）:

仓库是存放镜像的地方。仓库分为公有仓库（Docker Hub，阿里云）和私有仓库。

2.2 docker的安装

主要参阅docker官网的文档，写得很详细，现在需要挂梯子访问：Install Docker Engine | Docker Docs。

如果是Centos系统，在执行下面的命令时会出错，因为Centos8于2021年年底停止了服务。

sudo yum install -y yum-utils

可以查看对应解决办法：问题解决：Failed to download metadata for repo ‘appstream‘: Cannot prepare internal mirrorlist:…-腾讯云开发者社区-腾讯云 (tencent.com)

同时注意要在docker配置中添加阿里的镜像加速源:容器镜像服务 (aliyun.com)

#常见的docker命令
systemctl start docker #启动docker服务
systemctl restart docker #重启docker服务
systemctl status docker #查看docker服务的状态
docker version #获取docker客户端和服务器的版本信息
docker images #列出本地主机上存在的docker镜像

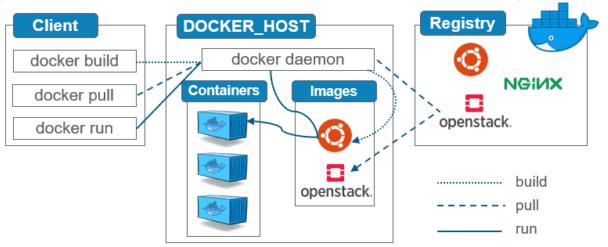
2.3 docker run的流程及原理

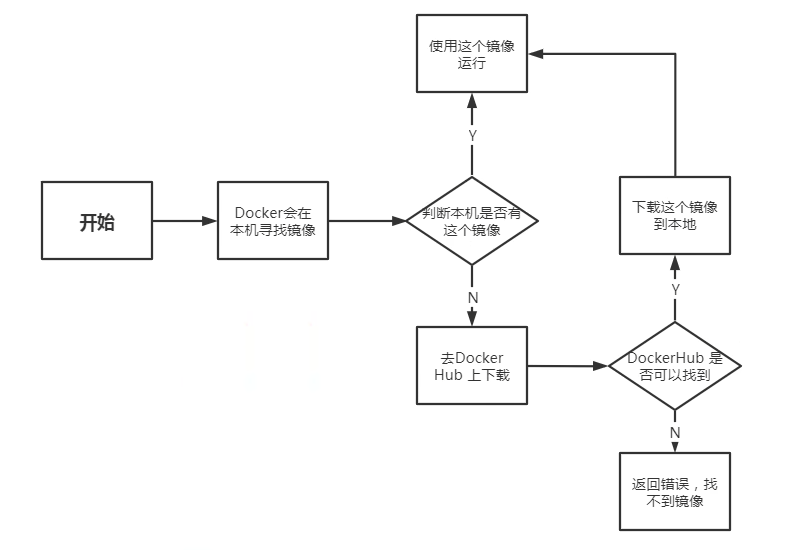
docker是一个Client-Server结构的系统，docker的守护进程运行在服务器上，通过socket从客户端访问。docker-server接收到docker-client的指令，就会执行这个指令。

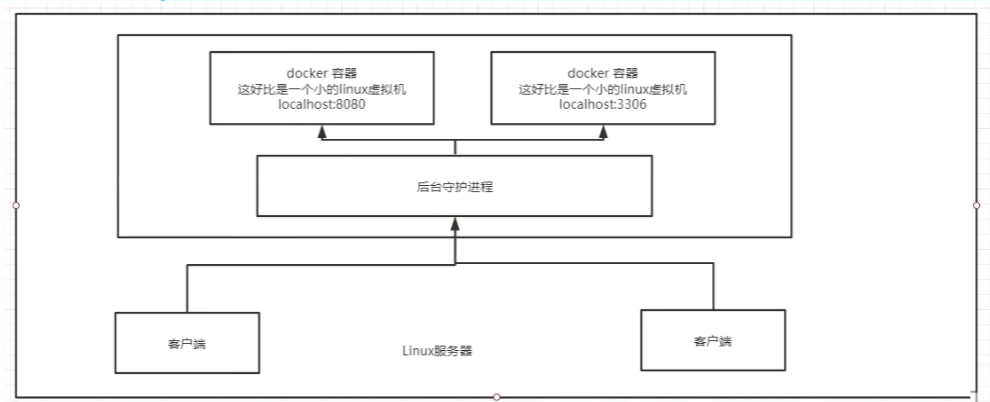
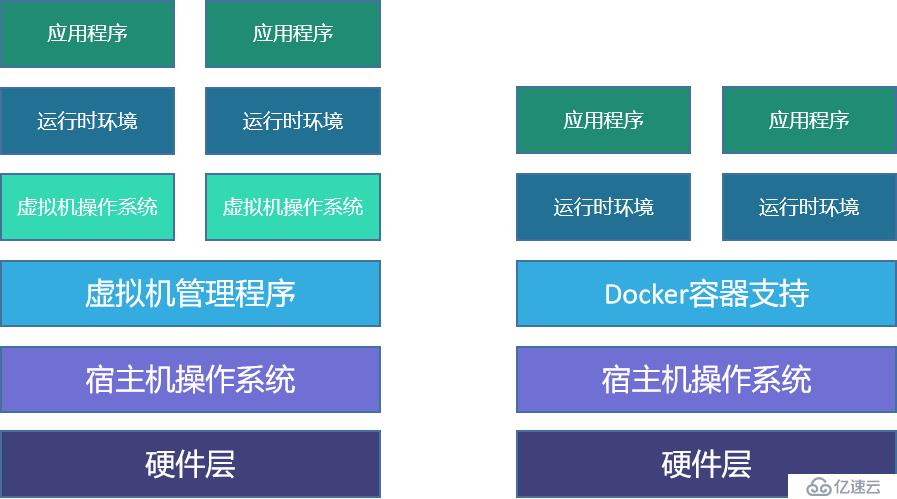
docker为什么比虚拟机VM快？

1. docker有着比虚拟机更少的抽象层。
2. docker利用的是宿主机的内核，vm利用的是虚拟机操作系统。

2.4 docker的常用命令

2.4.1 镜像命令

docker images #查看本地的所有镜像
docker search * #查找仓库中的镜像
docker pull * #下载镜像
docker pull mysql:版本号 #下载指定版本的镜像
docker rmi -f 镜像的名字/镜像的ID #删除镜像

2.4.2 容器命令

我们有了镜像才可以创建容器

docker run [可选参数] image #新建容器并启动
#参数说明
--name="xxx" 容器名字，用以区分容器
-d           后台方式运行
-it          使用交互方式运行，进入容器查看内容
-p           小写p，指定容器的端口
	-p 主机端口：容器端口（常用的端口映射）
	-p 容器端口
-P           大写P，随机指定容器的端口

exit #从容器中退出
Ctrl + P + Q #容器不停止并退出
docker rm 容器id #删除指定容器
docker rm -f $(docker ps -aq) #删除所有容器 

docker ps #列出所有运行中的容器
docker ps -a #查看所有已创建的容器

docker start 容器id   #启动容器,start是启动，run是创建一个全新的容器
docker restart 容器id #重启容器
docker stop 容器id    #停止当前正在运行的容器
docker kill 容器id    #强制停止当前容器

2.4.3 其他常用命令

docker run -d 镜像名 #后台启动容器
#容器使用后台运行，就必须要有一个前台进程，否则就会自动停止

docker logs -tf 容器id #查看日志

docker inspect 容器id #查看容器的元数据

docker exec -it 容器id /bin/bash #进入当前正在运行的容器（常用），开启一个新的终端
docker attach 容器id #也是进入当前正在运行的容器，但会进入正在执行的终端

docker cp 容器id：容器内路径  目的的主机路径 #拷贝容器内的文件到主机

2.5 docker实战练习

安装nginx

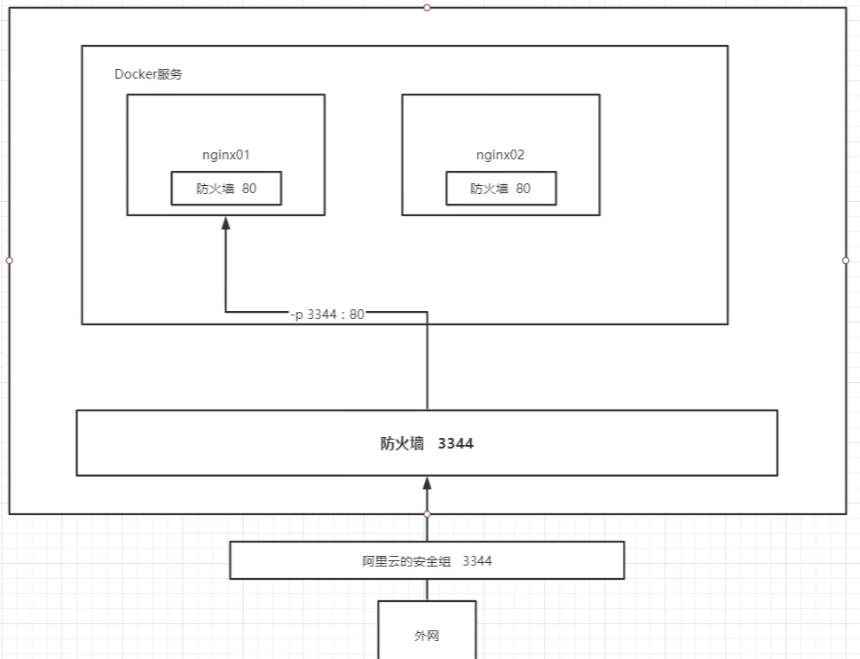
docker pull nginx
docker run -d --name nginx01 -p 3344:80 nginx #后台方式运行，服务名为nginx01，主机端口3344映射到容器内的80端口

• 公网访问 服务器地址：3344，需确保本地防火墙开放3344端口（默认防火墙关闭），同时服务器提供商的安全组开放3344端口（除22的ssh和3389的远程桌面连接，默认拒绝其他端口请求）。

Portainer可视化界面

docker run -d -p 8088:9000 --restart=always -v /var/run/docker.sock:/var/run/docker.sock --privileged=true portainer/portainer #安装docker的可视化管理界面

总结

下周计划：在机器学习部分，继续学习下一章节的内容。在docker学习部分，尝试打包在conda虚拟环境中已部署好的深度学习项目，并在服务器上部署。