pytorch_lesson4 张量的线性代数运算(矩阵的形变及特殊矩阵构造方法+矩阵的基本运算+矩阵的线性代数运算+矩阵的分解)

斯外戈的小白

已于 2022-05-09 17:52:34 修改

阅读量1.4k

点赞数 2

文章标签：线性代数 pytorch python

于 2022-05-09 16:31:47 首次发布

本文链接：https://blog.csdn.net/weixin_51589123/article/details/124665358

版权

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

前言

也就是PyTorch中BLAS和LAPACK模块的相关运算

一、BLAS和LAPACK概览

BLAS（Basic Linear Algeria Subprograms）和LAPACK（Linear Algeria Package）模块提供了完整的线性代数基本方法，由于涉及到函数种类较多，因此此处对其进行简单分类，具体包括：

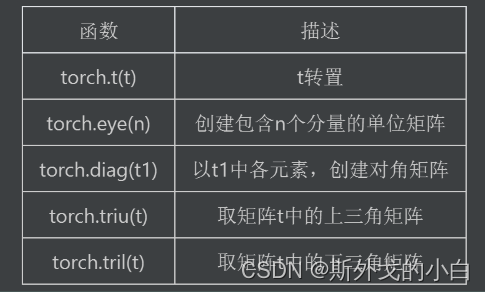
1、矩阵的形变及特殊矩阵的构造方法：包括矩阵的转置、对角矩阵的创建、单位矩阵的创建、上/下三角矩阵的创建等；
2、矩阵的基本运算：包括矩阵乘法、向量内积、矩阵和向量的乘法等，当然，此处还包含了高维张量的基本运算，将着重探讨矩阵的基本3、运算拓展至三维张量中的基本方法；
4、矩阵的线性代数运算：包括矩阵的迹、矩阵的秩、逆矩阵的求解、伴随矩阵和广义逆矩阵等；
5、矩阵分解运算：特征分解、奇异值分解和SVD分解等。

二、矩阵的形变及特殊矩阵构造方法

tensor矩阵运算
在这里插入图片描述

import torch
import numpy as np
#创建一个2*3矩阵
t1 = torch.arange(1, 7).reshape(2, 3).float()
print(t1)
'''
tensor([[1., 2., 3.],
        [4., 5., 6.]])
'''

#转置
print(torch.t(t1))
'''
tensor([[1., 4.],
        [2., 5.],
        [3., 6.]])
'''

print(t1.t())
'''
tensor([[1., 4.],
        [2., 5.],
        [3., 6.]])
'''
#矩阵的转置就是每个元素行列位置互换

print(torch.eye(3))
#制作一个三维的单位向量
'''
tensor([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.]])
'''
t = torch.arange(5)
print(torch.diag(t)) #将t中的元素创建为对角矩阵
'''
tensor([[0, 0, 0, 0, 0],
        [0, 1, 0, 0, 0],
        [0, 0, 2, 0, 0],
        [0, 0, 0, 3, 0],
        [0, 0, 0, 0, 4]])
'''
print(torch.diag(t, 1)) #对角矩阵中的对角线向上偏移一位
'''
tensor([[0, 0, 0, 0, 0, 0],
        [0, 0, 1, 0, 0, 0],
        [0, 0, 0, 2, 0, 0],
        [0, 0, 0, 0, 3, 0],
        [0, 0, 0, 0, 0, 4],
        [0, 0, 0, 0, 0, 0]])
'''
print(torch.diag(t, -1)) #对角矩阵中的对角线向下偏移一位
'''
tensor([[0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0],
        [0, 1, 0, 0, 0, 0],
        [0, 0, 2, 0, 0, 0],
        [0, 0, 0, 3, 0, 0],
        [0, 0, 0, 0, 4, 0]])
'''

t1 = torch.arange(9).reshape(3, 3)
print(t1)
'''
tensor([[0, 1, 2],
        [3, 4, 5],
        [6, 7, 8]])
'''

#取上三角矩阵
print(torch.triu(t1))
'''
tensor([[0, 1, 2],
        [0, 4, 5],
        [0, 0, 8]])
'''

#上三角矩阵向左下偏移一位
print(torch.triu(t1, -1))
'''
tensor([[0, 1, 2],
        [3, 4, 5],
        [0, 7, 8]])
'''
#上三角矩阵向右上偏移一位
print(torch.triu(t1, 1))
'''
tensor([[0, 1, 2],
        [0, 0, 5],
        [0, 0, 0]])
'''

#取下三角矩阵
print(torch.tril(t1))
'''
tensor([[0, 0, 0],
        [3, 4, 0],
        [6, 7, 8]])
'''

三、矩阵的基本运算

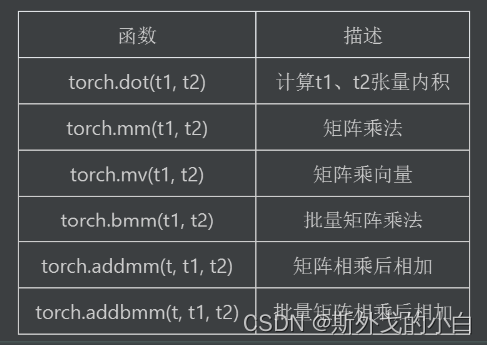
在这里插入图片描述

dot\vdot：点积计算

注意，在PyTorch中，dot和vdot只能作用于一维张量，且对于数值型对象，二者计算结果并没有区别，两种函数只在进行复数运算时会有区别。

t = torch.arange(1, 4)
print(t)
#tensor([1, 2, 3])
print(torch.dot(t, t)) #tensor(14)
print(torch.vdot(t, t)) #tensor(14)

#注意：dot/vdot不能对一维张量以外的张量进行计算，否则会报错

mm：矩阵乘法

t1 = torch.arange(1, 7).reshape(2, 3)
print(t1)
'''
tensor([[1, 2, 3],
        [4, 5, 6]])
'''
t2 = torch.arange(1, 10).reshape(3, 3)
print(t2)
'''
tensor([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
'''

#对应位置元素相乘
print(t1 * t1)
'''
tensor([[ 1,  4,  9],
        [16, 25, 36]])
'''

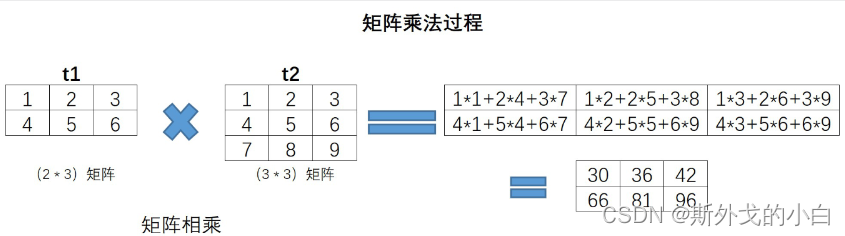
#矩阵乘法
print(torch.mm(t1, t2))
'''
tensor([[30, 36, 42],
        [66, 81, 96]])
'''

在这里插入图片描述

mv：矩阵和向量相乘

PyTorch中提供了一类非常特殊的矩阵和向量相乘的函数，矩阵和向量相乘的过程我们可以看成是先将向量转化为列向量然后再相乘。

met = torch.arange(1, 7).reshape(2, 3)
print(met)
'''
tensor([[1, 2, 3],
        [4, 5, 6]])
'''

vec = torch.arange(1, 4)
print(vec)
#tensor([1, 2, 3])
print(torch.mv(met, vec))
#tensor([14, 32])
print(torch.mm(met, vec.reshape(3, 1))) #将vec转变为矩阵之后就得用mm矩阵相乘了
'''
tensor([[14],
        [32]])
'''
print(torch.mm(met, vec.reshape(3, 1)).flatten())
#tensor([14, 32])

理解：mv函数本质上提供了一种二维张量和一维张量相乘的方法，在线性代数运算过程中，有很多矩阵乘向量的场景，典型的如线性回归的求解过程，通常情况下我们需要将向量转化为列向量（或者某些编程语言就默认向量都是列向量）然后进行计算，但PyTorch中单独设置了一个矩阵和向量相乘的方法，从而简化了行/列向量的理解过程和将向量转化为列向量的转化过程。

bmm：批量矩阵相乘

t3 = torch.arange(1, 13).reshape(3, 2, 2)
print(t3)
'''
tensor([[[ 1,  2],
         [ 3,  4]],

        [[ 5,  6],
         [ 7,  8]],

        [[ 9, 10],
         [11, 12]]])
'''

t4 = torch.arange(1, 19).reshape(3, 2, 3)
print(t4)
'''
tensor([[[ 1,  2,  3],
         [ 4,  5,  6]],

        [[ 7,  8,  9],
         [10, 11, 12]],

        [[13, 14, 15],
         [16, 17, 18]]])
'''


print(torch.bmm(t3, t4))
'''
tensor([[[ 1,  2,  3],
         [ 4,  5,  6]],

        [[ 7,  8,  9],
         [10, 11, 12]],
'''

注意：
1、三维张量内包括的二维张量的个数要一致；
2、每个内部矩阵，需要满足矩阵乘法的条件，也就是左乘矩阵的行数要等于右乘矩阵的列数

addmm：矩阵相乘后相加

addmm函数结构：addmm(input, mat1, mat2, beta=1, alpha=1)
输出结果：beta * input + alpha * (mat1 * mat2)

t = torch.arange(3)
print(t)
#tensor([0, 1, 2])
print(torch.mm(t1, t2))
'''
tensor([[30, 36, 42],
        [66, 81, 96]])
'''
print(torch.addmm(t, t1, t2))
'''
tensor([[30, 37, 44],
        [66, 82, 98]])
'''

print(torch.addmm(t, t1, t2, beta=0, alpha=10))
'''
tensor([[300, 360, 420],
        [660, 810, 960]])
'''

addbmm：批量矩阵相乘后相加

t = torch.arange(6).reshape(2, 3)
print(t)
'''
tensor([[0, 1, 2],
        [3, 4, 5]])
'''

print(t3)
'''
tensor([[[ 1,  2],
         [ 3,  4]],

        [[ 5,  6],
         [ 7,  8]],

        [[ 9, 10],
         [11, 12]]])
'''

print(t4)
'''
tensor([[[ 1,  2,  3],
         [ 4,  5,  6]],

        [[ 7,  8,  9],
         [10, 11, 12]],

        [[13, 14, 15],
         [16, 17, 18]]])
'''

print(torch.bmm(t3, t4))
'''
tensor([[[  9,  12,  15],
         [ 19,  26,  33]],

        [[ 95, 106, 117],
         [129, 144, 159]],

        [[277, 296, 315],
         [335, 358, 381]]])
'''

print(torch.addbmm(t, t3, t4))
'''
tensor([[381, 415, 449],
        [486, 532, 578]])
'''

注：addbmm会在原来三维张量基础之上，对其内部矩阵进行求和

四、矩阵的线性代数运算

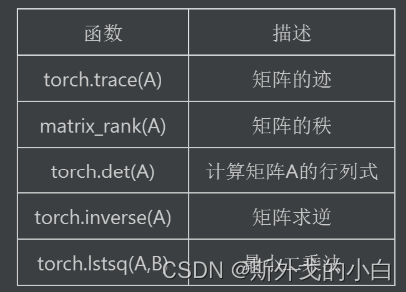
在这里插入图片描述

1.矩阵的迹（trace）

矩阵的迹的运算相对简单，就是矩阵对角线元素之和，在PyTorch中，可以使用trace函数进行计算。

A = torch.tensor([[1, 2], [3, 4]], dtype=torch.float32)
print(A)
'''
tensor([[1., 2.],
        [3., 4.]])
'''
print(torch.trace(A))
#tensor(5.)

#对于矩阵的迹来说，计算过程不需要是方阵
B = torch.arange(1, 7).reshape(2, 3)
print(B)
'''
tensor([[1, 2, 3],
        [4, 5, 6]])
'''
print(torch.trace(B))
#tensor(6)

2.矩阵的秩(rank)

矩阵的秩（rank），是指矩阵中行或列的极大线性无关数，且矩阵中行、列极大无关数总是相同的，任何矩阵的秩都是唯一值，满秩指的是方阵（行数和列数相同的矩阵）中行数、列数和秩相同，满秩矩阵有线性唯一解等重要特性，而其他矩阵也能通过求解秩来降维，同时，秩也是奇异值分解等运算中涉及到的重要概念。

matrix_rank计算矩阵的秩

A = torch.arange(1, 5).reshape(2, 2).float()
print(A)
'''
tensor([[1., 2.],
        [3., 4.]])
'''

print(torch.matrix_rank(A))
#tensor(2)


B = torch.tensor([[1, 2], [2, 4]]).float()
print(B)
print(torch.matrix_rank(B))
'''
tensor([[1., 2.],
        [2., 4.]])

3.矩阵的行列式(det)

所谓行列式，我们可以简单将其理解为矩阵的一个基本性质或者属性，通过行列式的计算，我们能够知道矩阵是否可逆，从而可以进一步求解矩阵所对应的线性方程。当然，更加专业的解释，行列式的作为一个基本数学工具，实际上就是矩阵进行线性变换的伸缩因子。

在这里插入图片描述
更为简单的情况，如果对于一个2*2的矩阵，行列式的计算就是主对角线元素之积减去另外两个元素之积

A = torch.tensor([[1, 2], [4, 5]]).float()     # 秩的计算要求浮点型张量
print(A)
'''
tensor([[1., 2.],
        [4., 5.]])
'''

print(torch.det(A))
#tensor(-3.)

print(B)
'''
tensor([[1., 2.],
        [2., 4.]])
'''

print(torch.det(B))
#tensor(-0.)

在这里插入图片描述
行列式的计算，要求二维张量必须是方正，也就是行列数必须一致，否则会报错

4.线性方程组的矩阵表达形式

在正式进入到更进一步矩阵运算的讨论之前，我们需要对矩阵建立一个更加形象化的理解。通常来说，我们会把高维空间中的一个个数看成是向量，而由这些向量组成的数组看成是一个矩阵。例如：（1，2），（3，4）是二维空间中的两个点，矩阵A就代表这两个点所组成的矩阵。

import matplotlib as mpl
import matplotlib.pyplot as plt

#绘制点图查看两个点的位置
plt.plot(A[:, 0], A[:, 1], 'o')
plt.show()

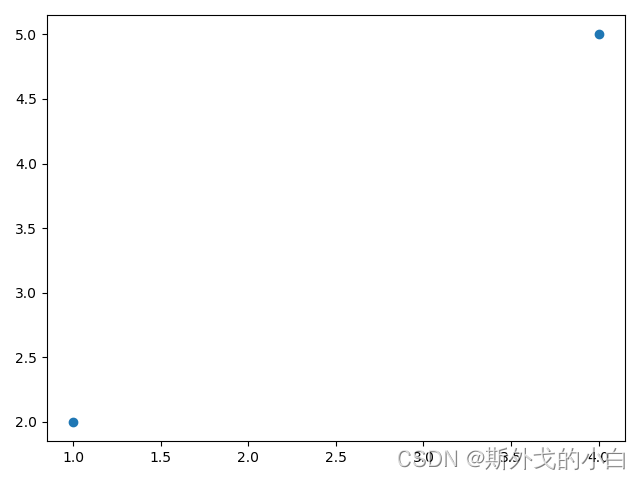
在这里插入图片描述

如果更进一步，我们希望在二维空间中找到一条直线，来拟合这两个点，也就是所谓的构建一个线性回归模型，我们可以设置线性回归方程如下
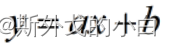
在这里插入图片描述
带入（1，2）和（3，4）两个点之后，我们还可以进一步将表达式改写成矩阵表示形式，改写过程如下

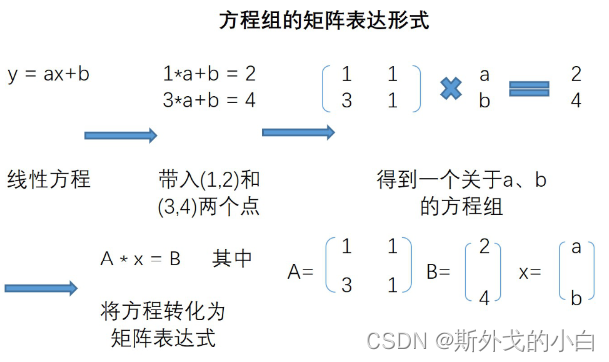
有了A的逆，我们就可以求出来权重矩阵，即：

在上述线性方程组求解场景中，我们已经初步看到了逆矩阵的用途，而一般来说，我们往往会通过伴随矩阵来进行逆矩阵的求解。由于伴随矩阵本身并无其他核心用途，且PyTorch中也未给出伴随矩阵的计算函数（目前），因此我们直接调用inverse函数来进行逆矩阵的计算。
在这里插入图片描述

inverse函数：求解逆矩阵

A = torch.tensor([[1.0, 1], [3, 1]])
print(A) #前面的[1, 1]是为了乘以偏置b而设置的

B = torch.tensor([2., 4.])

#然后用inverse函数求解额逆矩阵
print(torch.inverse(A))
'''
tensor([[ 1.0000e+00, -5.9605e-08],
        [-5.9605e-08,  1.0000e+00]]
'''
E = torch.mm(torch.inverse(A), A)
print(E)
'''
tensor([[ 1.0000e+00, -5.9605e-08],
        [-5.9605e-08,  1.0000e+00]]
'''
#之所以跟单位矩阵不一样，是因为pytorch本身计算精度带来的问题，因为数值较小，所以基本可以等同于0

#由于权重矩阵等于A的逆点成B矩阵
W = torch.mv(torch.inverse(A), B)
print(W)
#tensor([1.0000, 1.0000]) 说明a=1，b=1. y=ax+b过两点，验证成功

五、矩阵的分解

#运算中的常规计算，矩阵分解也有很多种类，常见的例如QR分解、LU分解、特征分解、SVD分解等等，虽然大多数情况下，矩阵分解都是在形式上将矩阵拆分成几种特殊矩阵的乘积，但本质上，矩阵的分解是去探索矩阵更深层次的一些属性。本节将主要围绕特征分解和SVD分解展开讲解，更多矩阵分解的运算，我们将在后续课程中逐渐进行介绍。值得一提的是，此前的逆矩阵，其实也可以将其看成是一种矩阵分解的方式，分解之后的等式如下：
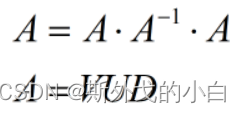
在这里插入图片描述

1.特征分解

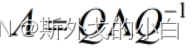
在这里插入图片描述
Q的列是A的特征值所对应的特征向量；中间的矩阵是矩阵A的特征值按照降序排列组成的对角矩阵

torch.eig函数：特征分解

A = torch.arange(1, 10).reshape(3, 3).float()
print(A)

print(torch.eig(A, eigenvectors=True))  # 注，此处需要输入参数为True才会返回矩阵的特征向量
'''
eigenvalues=tensor([[ 1.6117e+01,  0.0000e+00],
        [-1.1168e+00,  0.0000e+00],
        [ 2.9486e-07,  0.0000e+00]]),
eigenvectors=tensor([[-0.2320, -0.7858,  0.4082],
        [-0.5253, -0.0868, -0.8165],
        [-0.8187,  0.6123,  0.4082]]))
'''

输出结果中，eigenvalues表示特征值向量，即A矩阵分解后的Λ矩阵的对角线元素值，并按照又大到小依次排列，eigenvectors表示A矩阵分解后的Q矩阵，此处需要理解特征值，所谓特征值，可简单理解为对应列在矩阵中的信息权重，如果该列能够简单线性变换来表示其他列，则说明该列信息权重较大，反之则较小。特征值概念和秩的概念有点类似，但不完全相同，矩阵的秩表示矩阵列向量的最大线性无关数，而特征值的大小则表示某列向量能多大程度解读矩阵列向量的变异度，即所包含信息量，秩和特征值关系可用下面这个例子来进行解读。

B = torch.tensor([1, 2, 2, 4]).reshape(2, 2).float()
print(B)
#tensor(1)
print(torch.matrix_rank(B))
'''
tensor([[1., 2.],
        [2., 4.]])
'''

print(torch.eig(B))
'''
eigenvalues=tensor([[0., 0.],
        [5., 0.]]),
eigenvectors=tensor([]))
'''
#返回结果只有一个特征

2.奇异值分解（SVD）

由于特征分解只能作用于方阵，而大多数实际情况下矩阵行列数未必相等，此时要进行类似的操作就需要采用和特征值分解思想类似的奇异值分解（SVD）

奇异值分解（SVD）来源于代数学中的矩阵分解问题，对于一个方阵来说，我们可以利用矩阵特征值和特征向量的特殊性质（矩阵点乘特征向量等于特征值数乘特征向量），通过求特征值与特征向量来达到矩阵分解的效果
在这里插入图片描述
U和V是两个正交矩阵，其中每一行（每一列）分别被称为左奇异向量和右奇异向量。
本质上来讲，奇异值分解就是为了挑选重要的特征向量，去掉不重要的信息。

C = torch.tensor([[1, 2, 3], [2, 4, 6], [3, 6, 9]]).float()
print(C)
'''
tensor([[1., 2., 3.],
        [2., 4., 6.],
        [3., 6., 9.]])
'''
print(torch.svd(C))
'''
U=tensor([[-2.6726e-01,  9.6362e-01, -3.7767e-08],
        [-5.3452e-01, -1.4825e-01, -8.3205e-01],
        [-8.0178e-01, -2.2237e-01,  5.5470e-01]]),
S=tensor([1.4000e+01, 4.2751e-08, 1.6397e-15]),
V=tensor([[-0.2673, -0.9636,  0.0000],
        [-0.5345,  0.1482, -0.8321],
        [-0.8018,  0.2224,  0.5547]]))
'''
#从结果上可以看出，我们的
cu, cs, cv = torch.svd(C)
#验证svd分解
print(torch.diag(cs))
'''
tensor([[1.4000e+01, 0.0000e+00, 0.0000e+00],
        [0.0000e+00, 4.2751e-08, 0.0000e+00],
        [0.0000e+00, 0.0000e+00, 1.6397e-15]])
'''
#我们可以看出来，只有一个特征值的数值较大，也就说明用一列基本上可以表示整个矩阵
print(torch.mm(torch.mm(cu, torch.diag(cs)), cv.t()))
'''
tensor([[1.0000, 2.0000, 3.0000],
        [2.0000, 4.0000, 6.0000],
        [3.0000, 6.0000, 9.0000]])
'''

此时我们可以根据svd输出结果对c进行降维，此时c可以只保留第一列（因为右面的奇异值过小）

u1 = cu[:, 0].reshape(3, 1)
print(u1)
'''
tensor([[-0.2673],
        [-0.5345],
        [-0.8018]])
'''
cs = cs[0]
print(cs)
#tensor(14.0000)

cv = cv[:, 0].reshape(1, 3)
print(cv)
#tensor([[-0.2673, -0.5345, -0.8018]])
print(torch.mm((u1 * cs), cv))
'''
tensor([[1.0000, 2.0000, 3.0000],
        [2.0000, 4.0000, 6.0000],
        [3.0000, 6.0000, 9.0000]])
'''

总结

提示：这里对文章进行总结：
例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。

斯外戈的小白

关注

2
点赞
踩
6

收藏

觉得还不错? 一键收藏
0
评论
pytorch_lesson4 张量的线性代数运算(矩阵的形变及特殊矩阵构造方法+矩阵的基本运算+矩阵的线性代数运算+矩阵的分解)

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、pandas是什么？二、使用步骤1.引入库2.读入数据总结前言提示：这里可以添加本文要记录的大概内容：例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。提示：以下是本篇文章正文内容，下面案例可供参考一、pandas是什么？示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。二、使用步骤1.引入库代.
复制链接

扫一扫

pytorch_lesson4 张量的线性代数运算(矩阵的形变及特殊矩阵构造方法+矩阵的基本运算+矩阵的线性代数运算+矩阵的分解)

文章目录

前言

一、BLAS和LAPACK概览

二、矩阵的形变及特殊矩阵构造方法

三、矩阵的基本运算

dot\vdot：点积计算

mm：矩阵乘法

mv：矩阵和向量相乘

bmm：批量矩阵相乘

addmm：矩阵相乘后相加

addbmm：批量矩阵相乘后相加

四、矩阵的线性代数运算

1.矩阵的迹（trace）

2.矩阵的秩(rank)

matrix_rank计算矩阵的秩

3.矩阵的行列式(det)

4.线性方程组的矩阵表达形式

inverse函数：求解逆矩阵

五、矩阵的分解

1.特征分解

torch.eig函数：特征分解

2.奇异值分解（SVD）

总结

“相关推荐”对你有帮助么？