Topsis与熵权法

定义

熵权法是一种客观赋权方法。
原理：指标的变异程度（方差）越小，所反映的信息量也越少，其对应的权值也应该越低。（客观 = 数据本身就可以告诉我们权重）

如何度量信息量的大小

通过上面的例子我们可以看出，越有可能发生的事情，信息量越少；越不可能发生的事情，信息量就越多。如果用概率表示的话，即概率越大，信息量越少，概率越小，信息量越大。
如果把信息量用I表示，概率用p表示，那么我们就可以建立一个函数关系:

假设x表示事件X可能发生的某种情况，p(x)表示这种情况发生的概率，则我们可以定义为：

信息熵

假设x表示事件X可能发生的某种情况，p(x)表示这种情况发生的概率。

注：当p(x)均为1/n时，H(x)取最大值，此时H(x) = ln n。

算法步骤

1.判断输入的矩阵中是否存在负数，如果有则要重新标准化到非负区间(后面计算概率时需要保证每一个元素为非负数)。

2.计算第j项指标下第i个样本所占的比重，并将其看作相对熵计算中用到的概率。

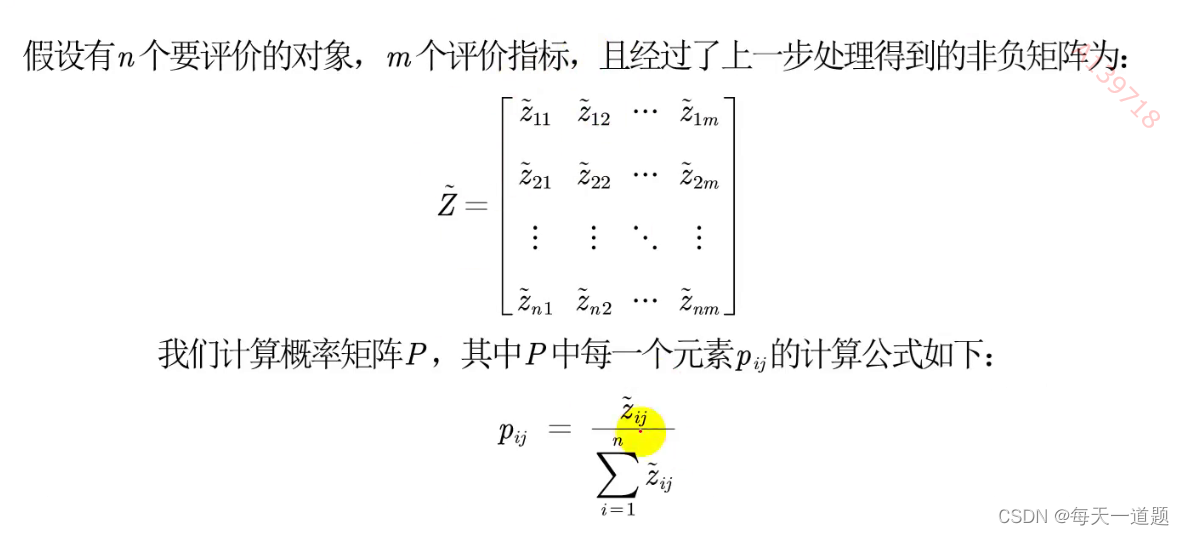
3.计算每个指标的信息熵，并计算信息效用值，并归一化得到每个指标的熵权。

代码

计算熵权：

function [W] = Entropy_Method(Z)
% 计算有n个样本，m个指标的样本所对应的的熵权
% 输入
% Z ： n*m的矩阵（要经过正向化和标准化处理，且元素中不存在负数）
% 输出
% W：熵权，1*m的行向量

%% 计算熵权
    [n,m] = size(Z);
    D = zeros(1,m);  % 初始化保存信息效用值的行向量
    for i = 1:m
        x = Z(:,i);  % 取出第i列的指标
        p = x / sum(x);
        % 注意，p有可能为0，此时计算ln(p)*p时，Matlab会返回NaN，所以这里我们自己定义一个函数
        e = -sum(p .* mylog(p)) / log(n); % 计算信息熵
        D(i) = 1- e; % 计算信息效用值
    end
    W = D ./ sum(D);  % 将信息效用值归一化，得到权重    
end

由于担心概率为0自己定义的函数：

% 重新定义一个mylog函数，当输入的p中元素为0时，返回0
function [lnp]