线性回归模型损失和优化

最新推荐文章于 2024-06-06 23:15:00 发布
最新推荐文章于 2024-06-06 23:15:00 发布
阅读量1.9k 收藏 2
点赞数 1
分类专栏： 机器学习基本算法 文章标签： 线性回归 算法 机器学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_51756104/article/details/121286363
版权
本文对比了正规方程与梯度下降在小规模和大规模数据学习任务中的应用，详细解释了正规方程的一次求解优点和在复杂特征下的局限，以及梯度下降的迭代优化过程。讨论了如何根据数据规模选择合适的方法：正规方程适用于简单线性回归，而梯度下降在大规模数据下通过SGDRegressor更有效。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

性回归模型损失和优化

学习任务

使用正规方程对损失函数优化的过程
使用梯度下降法对损失函数优化的过程

在这里插入图片描述

优化方法

正规方程

正规方程,一次就可以求得最合适的值
在这里插入图片描述
理解：X为特征矩阵，y为目标值矩阵。直接求得最好的结果
缺点：当特征值过多复杂时，求解速度太慢并且得不到结果。

正规方程推导过程

在这里插入图片描述

梯度下降

     梯度是微积分中一个很重要的概念，在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率;在多变量函数中，梯度是一一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向;
    这也就说明了为什么我们需要千方百计的求取梯度!我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向
     就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的反方向一直走，就能走到局部的最低点!

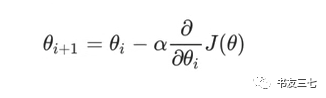
在这里插入图片描述
在这里插入图片描述

梯度下降公式

在这里插入图片描述

两者的对比

在这里插入图片描述

如何选择

小规模数据

    ·正规方程：LinearRegression（不能解决拟合问题）

    ·岭回归

大规模数据

·梯度下降法：SGDRegressor
人工智能类比赛从入门到精通 一
qq_39903036的博客
11-02 750
入门实战级比赛一前言1、赛题解读2、相关知识点2.1二分类问题2.1.1分类回归相关概念2.1.2 二分类评价指标2.1.3 二分类算法2.2 逻辑回归2.2.1 线性回归2.2.2 逻辑回归实战演练 前言 本篇文章是先进行赛题解读，然后介绍相关知识点，最后进行实战演练，此实战代码完全可应用到企业内部使用～ 1、赛题解读 本次进行的比赛是一个预测分析比赛，预测客户的购买行为，即银行的客服人员与客户进行至少一次的电话联系，以确认客户是否有意愿购买该银行的产品。 此次比赛的基本类型是分类任务，即预测客户是否购买
线性回归的损失和优化
lqq2578962384的博客
11-11 397
不看一定后悔的学习资料
线性回归，损失的定义，损失函数与优化方法，用统计学习方法来理解线性回归、损失函数和优化方法，Sklearn使用方法
ck784101777的博客
08-09 4941
目录 1.线性回归 一元线性关系 多元线性关系 2.损失：评估预测结果与真实值的偏差程度 误差累积的结果 总损失计算公式： 损失函数：最小二乘法 3.损失函数的优化方法 4.用统计学习方法来理解线性回归、损失函数和优化方法 5.Sklearn API接口与使用方式 波士顿房价预测案例 参考文档 1.线性回归 线性回归属于监督学习的回归问题的一类，由于回归问题的目标值是连续的，所以线性回归算法的目标是寻找连续的目标值之间的一种趋势，通过获取这种趋势来建立模型。得到测试集后，将特征值
线性回归---4.线性回归的损失和优化
singularity1980的博客
05-06 1383
1.什么是损失 真是值和预测值之间的误差 公式:最小二乘法 2.如何进行优化 第一种方法 正规方程 举例 详解: 1.特征值逆矩阵 乘 特征值原矩阵 乘 特征值逆矩阵 * 目标值矩阵 T 就是矩阵转置 -1就是逆矩阵 第二种方法 梯度下降 概念 梯度是微积分中一个很重要的概念 ​ 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率 ​ 在多变...
机器学习算法------2.4 线性回归的损失和优化（损失函数、优化算法、 正规方程、梯度下降）
程序猿-凡白的博客
07-17 1756
文章目录2.4 线性回归的损失和优化学习目标1 损失函数2 优化算法2.1 正规方程2.1.1 什么是正规方程2.1.2 正规方程求解举例2.1.3 正规方程的推导2.2 梯度下降(Gradient Descent)2.2.1 什么是梯度下降2.2.2 梯度的概念2.2.3 梯度下降举例2.2.4 梯度下降**（**Gradient Descent）公式3 梯度下降和正规方程的对比3.1 算法选择依据：4 小结 2.4 线性回归的损失和优化 学习目标 知道线性回归中损失函数 知道使用正规方程对损失函数优化
Python 机器学习 线性回归的损失和优化
weixin_42098295的博客
02-08 1213
机器学习中，线性回归是一种预测连续值的算法，例如房价、销售额等。线性回归模型试图找到一条直线（在多维空间中则是一个平面或超平面），这条直线能够尽可能准确地表示输入变量（特征）和输出变量（目标值）之间的关系。模型的损失（Loss）和优化（Optimization）是建立有效线性回归模型的两个关键方面。
第4章 回归与聚类算法 2 4.1. 线性回归 2 4.1.1. 线性回归的原理 2 4.1.2. 线性回归的损失和优化原理（理
05-21
4.5.1节讲解了sklearn库中保存和加载模型的API，4.5.2节给出了线性回归模型保存加载的实例，这样可以确保模型训练的结果能够在后续使用中复用。 无监督学习在4.6节被提及，尤其是K-means聚类算法，它是无监督学习中...
线性回归：损失函数.pdf
最新发布
05-14
线性回归模型可以简单分为简单线性回归和多元线性回归，简单线性回归只涉及一个自变量和一个因变量之间的关系，而多元线性回归则涉及多个自变量。当特征数量较多时，为了防止过拟合，可以引入正则化项（如L1、L2正则...
线性回归模型详解
码上飞扬的博客
06-06 5876
线性回归模型的目标是寻找最佳的线性组合来预测目标变量。具体来说，对于简单线性回归，模型试图找到一条最佳拟合直线，而对于多元线性回归，则是在多维空间中找到一个最佳拟合的超平面。多元线性回归模型可以表示为：其中，𝑌Y 是因变量，𝑋1,𝑋2,...,𝑋𝑛X1​,X2​,...,Xn​ 是自变量，𝛽0β0​ 是截距，𝛽1,𝛽2,...,𝛽𝑛β1​,β2​,...,βn​ 是每个自变量对应的斜率，表示其对𝑌Y的影响程度，而𝜖ϵ 是误差项，反映了模型未能解释的随机波动。
回归模型诊断与优化
weixin_44336181的博客
06-01 2010
文章目录 1、异方差 2、自相关 3、异常值 异方差：回归模型中的异方差（Heteroscedasticity）是指随机误差项的方差不是一个常数，儿是随着自变量的取值变化而变化 由于不满足回归分析中的同方差（Homoscedasticity）的前提假设，异方差将可能带来以下问题： 对使用最小二乘法求解参数时，参数估计是虽然无偏，但不是最小方差线性无偏估计 参数的显著性检验失效 回归方程的应用效果不理想 造成异方差的常见原因： 模型缺少了某些解释变量，缺省变量本身的方差被包含在了随机误差的方差中。 模型
机器学习01-(机器学习概述、数据预处理、线性回归，损失函数、梯度下降)
yegeli的博客
07-03 648
机器学习机器学习概述什么是机器学习为什么需要机器学习机器学习的问题机器学习的种类机器学习的一般过程机器学习的典型应用机器学习的基本问题数据预处理均值移除(标准化)范围缩放归一化二值化独热编码（onehot）标签编码回归模型线性回归 机器学习 概述 什么是机器学习 机器学习是一门能够让编程计算机从数据中学习的计算机科学。 一个计算机程序在完成任务T之后，获得经验E，其表现效果为P，如果任务T的性能表现，也就是用以衡量的P，随着E增加而增加，那么这样计算机程序就被称为机器学习系统。 自我完善，自我增进，自我适应
Linear Regression分析概率解释和SVD优化
xiaoxu1025的专栏
02-17 437
线性回归可以说是最简单模型。 给定训练数据 D={ xi, yi} i=1,2,...n，其中 ，回归学习一个从输入x 到输出y的映射 f 且f是一个线性函数y= f (x|w)=w.Tx 如果损失函数采用RSS J(w) = ∑(yi -w.Txi)^2 i=1,2...n 如果没有正则项就等价于最小二乘线性回归 正则项采用L2时得到Ridge回归模型，正则项为L1得到La...
（六）线性回归模型优化求解之‘梯度下降法’
fly_Xiaoma的博客
02-01 865
1、理解梯度下降法      2、梯度下降法和OLS的梯度下降      3、岭回归的梯度下降、Lasso      4、随机梯度下降法以及它的实现方法-SGDRegressor 随机梯度下降法：      SGDRegressor优化相关的参数：             ...
08线性回归+基础优化算法
qq_59414507的博客
01-06 948
08线性回归+基础优化算法
机器学习【2】：梯度下降算法，梯度下降实现简单回归案例
qq_36499794的博客
11-10 379
一. 梯度下降 1. 什么叫梯度下降？ 假设现在在一个二维空间，只有x,y坐标。我模拟一个简单的场景： 梯度下降法的基本思想可以类比为一个游客下山的过程。假如一个人被困在山上，需要下山(也就是找到山的最低点)。但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮...
Lecture3 损失函数和优化损失函数
pinkshell_1314的博客
08-19 1381
Lecture3 损失函数和优化损失函数
最优化算法之梯度下降法
tian_panda的博客
08-27 4296
0 前言     优化问题最常见的求解方式是迭代优化，常见的优化算法有梯度下降。因此来记录下梯度下降算法。 1  原理     优化的目标是损失函数最小化，函数的梯度方向代表了函数值增长最快的方向，那么和它相反的方向就是函数减少速度最快的方向。梯度下降的优化思想是用当前位置负梯度（相反方向）方向作为搜索方向，也称“最速下降法”。梯度下降法是迭代算法，每一步需要求解目标函数与梯度向量。   ...
Python-Level5-day02:回归问题:线性模型定义,训练(损失函数，梯度下降)；线性回归代码实现与评价指标；多项式回归模型定义与代码实现；过拟合欠拟合
dpq666dpq666
06-22 793
2022年7月9日16:42:52
源代码优化：线性与非线性回归模型探究
“优化源代码全集线性回归非线性回归模型”涉及了一系列复杂的概念，包括源代码优化、线性与非线性回归模型的理论和实操、以及代码管理和维护的最佳实践。通过这些知识点的综合应用，可以有效地提高机器学习模型的...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值