数值最优化---二阶条件

夏威夷大核桃

已于 2023-02-05 18:18:06 修改

阅读量647

点赞数

分类专栏：数值最优化文章标签：线性代数算法

于 2023-02-05 18:11:57 首次发布

本文链接：https://blog.csdn.net/weixin_51991224/article/details/128875052

版权

数值最优化专栏收录该内容

7 篇文章 0 订阅

订阅专栏

首先定义critical cone（绝对锥）：

这里我们有必要对critical cone的定义式进行说明，首先要明确的是，线性可行方向 $F(x^* )$ 是一些向量的集合，进而critical cone的含义是从线性可行方向 $F(x^* )$ 中，取出满足一定条件的一些向量。

取出的条件就是：关于给定最优点 $x^*$ 的有效集中的不等式约束 $A(x^*)\cap I$ 中对应的乘子 $\lambda _i >0$ 的全部约束，都有 $\triangledown c_i(x^*)^Tw=0$ ；

比如有效集中的不等式约束有四个（ $c_1 \quad c_2\quad c_3\quad c_4$ ），对应的 $\lambda_i^*$ 写在后面，如下所示：

$A(x^*)\cap I = \left\{\begin{matrix} c_1(x^*) = 0\quad\quad\lambda_1^*>0\\ c_2(x^*) = 0\quad\quad\lambda_2^*>0\\ c_3(x^*) = 0\quad\quad\lambda_3^*=0\\ c_4(x^*) = 0\quad\quad\lambda_4^*=0 \end{matrix}\right.$

因此对应的乘子 $\lambda_i>0$ 的约束就是约束1和约束2，判断一个向量 $w$ 是不是critical cone中的元素就是要判断：是否 $w^T\triangledown c_1(x^*) = w^T\triangledown c_2(x^*) =0$ 。

接下来，我们再来看 $w\in C(x^*,\lambda^*)$ 的等价表述就会变得很清晰：

从左到右：第一个和第三个等式是 $F(x^*)$ 的定义保证的，第二个等式是 $C(x^*,\lambda^*)$ 的定义保证的。

从右到左同理。

进而加上有效集之外的 $\lambda_i^* = 0$ 我们可以推出，对于全部约束这两部分的乘积总是零：

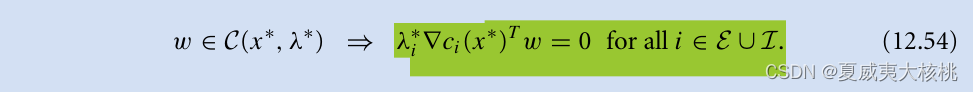
因此回到 $\L$ 的定义式12.33和KKT条件12.34a，

进而可以推得：

然后引入定理12.5（二阶必要条件）：

这个定理的证明在书上很清晰，就不再赘述。进而引入二阶充分条件：

首先是引入了一个 $C(x^*,\lambda^*)$ 的子集： $\bar{C} = \{d\in C(x^*,\lambda^*)\mid\left \| d \right \|=1 \}$ ，这个子集给出了一个模长的限制。

进而，在这个子集的基础上，引入一个正的最小值 $\sigma$ ：

我们要证明的就是在12.66成立的基础上: 对于当 $k$ 足够大时趋近于 $x^*$ 的任何可行点序列 $\{ z_k\}$ ，都会有：

$f(z_k) \geq f(x^*)+(\sigma /4)\left \| z_k-x^* \right \|^2$ ，当k足够大时

因此 $x^*$ 是极小值。

下面使用反证法：假设存在一个当 $k$ 足够大时趋近于 $x^*$ 的可行点序列 $\{ z_k\}$ ，当k足够大时，有 $f(z_k) < f(x^*)+(\sigma /4)\left \| z_k-x^* \right \|^2$ ：

进而令 $t_k = \left \| z_k-x^* \right \|$ ，我们可以给出一个属于切锥的方向向量 $d$ ：

由引理12.2的第一条，我们知道： $d\in F(x^*)$ 。

此外由于KKT条件和 $z_k$ 是可行点这两个已知条件，可以推得：

对于 $i\in \varepsilon :c_i(z_k) = 0$
对于 $i\in I :\lambda_i\geq 0$ 并且 $c_i(z_k)\geq 0$

因此有对于有效集中的约束来说 $\lambda_i^*c_i(z_k)$ 总是非负的，也就有：

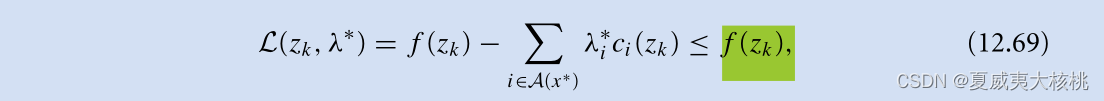
假设上面12.68所定义的向量 $d\notin C(x^*,\lambda^*)$ (这是一种情况，还有另一种情况是属于关系，要分别证伪才行)：

如果 $d\notin C(x^*,\lambda^*)$ ，那么回到 $C(x^*,\lambda^*)$ 的定义式就可以看出，一定存在某个约束 $j\in A(x^*)\cap I$ 使得 $\triangledown c_j(x^*)^Td>0$ 而不是 $\triangledown c_j(x^*)^Td=0$ ，所以再乘上KKT条件中的 $\lambda_j$ 就有：

然而对于有效集中的其他的约束，由于 $d\in F(x^*)$ ，则有：

我们对12.70式进行泰勒展开，并用到了12.68的一个代换，可得：

进而从12.69，我们有：

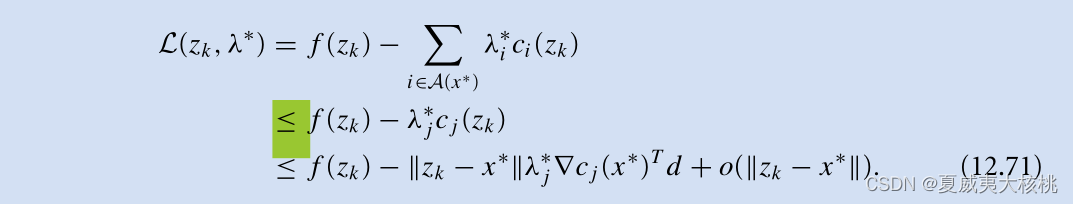
第一个不等号是因为相对于求和而去掉的所有累加项都是非负的。

然后将 $L(z_k,\lambda^*)$ 在 $(x^*,\lambda^*)$ 点展开：

等式右边第二项为零，第三项吸收到小项里，记作（这里我不太清楚这么理解对不对）：

$L(z_k,\lambda^*) = f(x^*)+ o(\left \| z_k-x^* \right \|)$

与12.71式合并可得：

这个式子，加上12.70，发现与反证法的假设相矛盾，因此 $d\notin C(x^*,\lambda^*)$ 这种情况的反证法不成立；

再对 $d\in F(x^*)$ 的情况进行讨论：

此时，有 $d\in C(x^*,\lambda^*)$ 并且 $d^T\triangledown ^2_{xx}L(x^*,\lambda^*)d\geq \sigma$ 。

简单的几步变换：

第一个不等式来自12.69 和 12.62的结合。

最后发现与大前提矛盾，因此第二种情况也假设失败。，综合两种情况，反证法证明结束。

这里容易产生疑惑的地方是在反证法中间又做了一个假设，然后把两个反证法嵌套在一起，很让人困惑，其实是这样的：

首先是最开始的反证法的假设，简单记作A=0；然后在后面的讨论时发现，在论证中存在一个向量 $d\in F(x^*)$ ，但是 $F(x^*)$ 分为两部分，因此 $d$ 也就存在两种情况：

$d\notin C(x^*,\lambda^*)$
$d\in C(x^*,\lambda^*)$

下面进行分类讨论：

对于第一种情况，正是书上花了很大篇幅论证的，发现与大前提A=0矛盾，但这时反证法还没有结束，因为还有第二种情况没有论证，讨论继续，后面又发现第二种情况也与大前提A=0矛盾，因此，大前提的假设错误，反证法结束。

因此，全部的论证过程并不是两个反证法嵌套，而是在反证法中存在一个分类讨论，进行分别论证了而已。

夏威夷大核桃

关注

0
点赞
踩
4

收藏

觉得还不错? 一键收藏
1
评论
数值最优化---二阶条件

对于第一种情况，正是书上花了很大篇幅论证的，发现与大前提A=0矛盾，但这时反证法还没有结束，因为还有第二种情况没有论证，讨论继续，后面又发现第二种情况也与大前提A=0矛盾，因此，大前提的假设错误，反证法结束。这里我们有必要对critical cone的定义式进行说明，首先要明确的是，线性可行方向。因此，全部的论证过程并不是两个反证法嵌套，而是在反证法中存在一个分类讨论，进行分别论证了而已。首先是最开始的反证法的假设，简单记作A=0；这个式子，加上12.70，发现与反证法的假设相矛盾，因此。
复制链接

扫一扫