谢尔宾斯基三角形本质上是分形。所谓分形是一个几何图形,它可以分为许多部分,每个部分皆是整体的缩小版。这个三角形的建立概念如下:
1.建立一个等边三角形,这个三角形称0阶(order=0)谢尔宾斯基三角形。
2.将三角形各边中点连接,称1阶谢尔宾斯基三角形。
3.中间三角形不变,将其他3个三角形各边中点连接,称2阶谢尔宾斯基三角形。
4.使用递归式函数概念,重复上述步骤,即可产生3阶、4阶级、或更高阶的谢尔宾斯基三角形。
# 谢尔宾斯基三角形,输入三角形的阶数,然后可用Turtle()绘出此三角形。
import time
import turtle
# 依据特定阶级数绘制Sierpinski三角形
def sierpinski(order, p1, p2, p3):
if order == 0:
# 将3个点连接绘制成三角形
drawLine(p1, p2)
drawLine(p2, p3)
drawLine(p3, p1)
else:
# 取得三角形各边长的中点
p12 = midpoint(p1, p2)
p23 = midpoint(p2, p3)
p31 = midpoint(p3, p1)
# 递归调用处理绘制三角形
sierpinski(order - 1, p1, p12, p31) # p1 、p2、p3三角形各中点连线得四个三角形,此处处理上面一个小三角形部分
sierpinski(order - 1, p12, p2, p23) # 此处处理左下角的一个小三角形部分
sierpinski(order - 1, p31, p23, p3) # 此处处理右下角的一个小三角形部分
# 绘制p1和p2之间的线条
def drawLine(p1, p2):
t.penup()
t.setpos(p1[0], p1[1])
t.pendown()
t.setpos(p2[0], p2[1])
t.penup()
t.seth(0)
# 传回2点的中间值
def midpoint(p1, p2):
p = [0, 0]
p[0] = (p1[0] + p2[0]) / 2
p[1] = (p1[1] + p2[1]) / 2
return p
t = turtle.Pen()
p1 = [0, 86.6]
p2 = [-100, -86.6]
p3 = [100, -86.6]
order = eval(input("输入阶数:"))
sierpinski(order, p1, p2, p3)
time.sleep(3)eval()函数
eval(<字符串>)能够以Python表达式的⽅式解析并执⾏字符串,并将返回结果输出。eval()函数将去掉字符串的两个引号,将其解释为⼀个变量。
作⽤:
a. 处理数字:
单引号,双引号,eval()函数都将其解释为int类型;三引号则解释为str类型。
b.处理字符串类型的字符串:
对于eval()括号中的的字符串(⾮数字),如果字符串带的是单引号或者是双引号都会引起NameError,这是因为eval()函数在处理字符串时会去掉其两个引号。正确应该使⽤⼀个单引号包含⼀个双引号组成的三引号来包含字符串。
这里的eval()函数也可以直接使用int(),也就是将输入的数字字符串转为整型数字。
绘图效果:
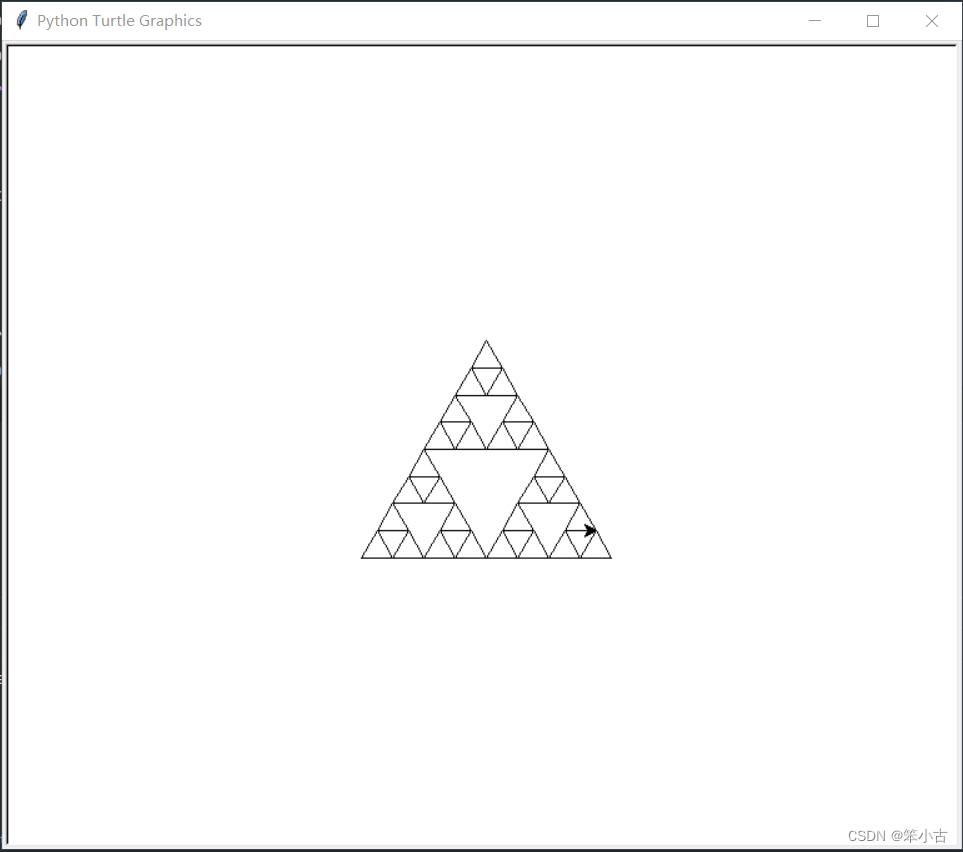








 这篇博客介绍了如何利用Python的turtle模块绘制谢尔宾斯基三角形,这是一种分形几何图形。通过递归函数实现不同阶数的三角形绘制,用户可以输入阶数来观察分形的细节。博客内容涉及Python编程、图形绘制和分形几何。
这篇博客介绍了如何利用Python的turtle模块绘制谢尔宾斯基三角形,这是一种分形几何图形。通过递归函数实现不同阶数的三角形绘制,用户可以输入阶数来观察分形的细节。博客内容涉及Python编程、图形绘制和分形几何。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










