【最优控制笔记】——2离散系统最优控制之不定终值

离散系统最优控制

说明：

在前述对终端状态确定情况的最优控制问题的基础上，进一步对终端状态不确定情况进行具体地讨论。

2.4 终端状态不确定——闭环控制

（2.4-1）思路：

类似的分析思路，我们还是根据Hamilton函数由式(2.2-5~8)可以得到状态、协状态和控制量的最初表达式：

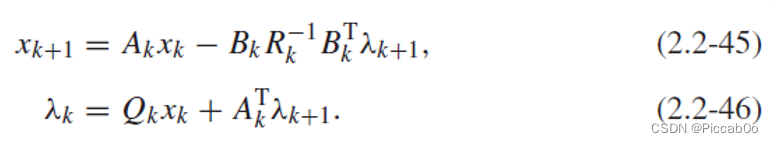
但，对于终端状态不确定情况的$x_N$，$d{x}_N\ne 0$，可以需要根据其边界条件：

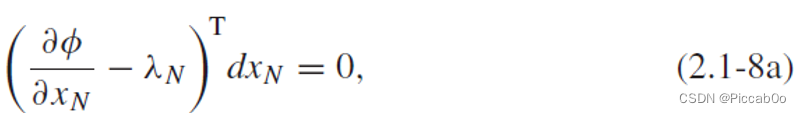
得到：

又根据性能指标中的终端状态权重项$\varphi =\frac{1}{2}{x}_N^{\mathrm{T}}{S}_N{x}_N$可得：

此处，不同于终端状态固定情况下状态和协状态解耦的形式，这里终端状态不固定时，状态和协状态耦合，很难求解。
但很容易看出，如果我们假设所有的${\lambda }_k$都满足式(2.2-49)的形式，即：

便使问题求解容易。因此，只需要找到${\lambda }_k$的一致表达形式即可。

（2.4-2）解决：

将式(2.2-50)代入状态$x_{k+1}$的表达式(2.2-45)得：

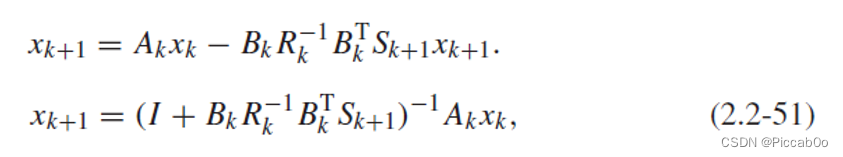
将式(2.2-50)代入协状态${\lambda }_k$的表达式(2.2-46)得：

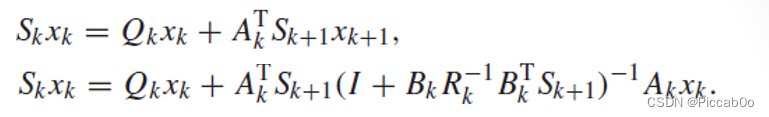
由于$x_k$往往非零，故两边可同除$x_k$，再利用matrix inversion lemma 可得：

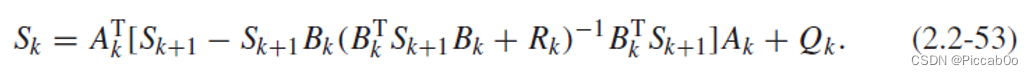
这说明$S_k$完全取决于系统的权重矩阵和$s_{k+1}$，因此${\lambda }_k$的形式满足，假设成立，可以基于此继续求解最优控制问题。

（2.4-3）最优控制问题求解：

上式(2.2-53)称为Riccati equation，如果$\forall k,|S_k|\ne 0$，可以继续用matrix inversion lemma改写：

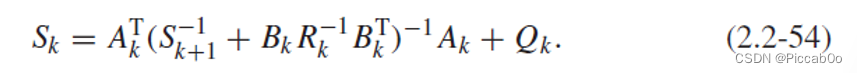
其代入式(2.2-51)可得状态轨迹$x_k$的迭代关系式。

进一步，考虑控制量$u_k$。由式(2.2-47)可得：

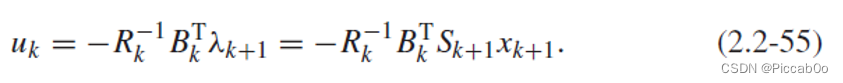
由于将$S_{k+1}$和$x_{k+1}$都带入数值求解太过于繁琐，因此，考虑将约束方程$x_{k+1}=A_k{x}_k+B_k{u}_k$代入，可得：

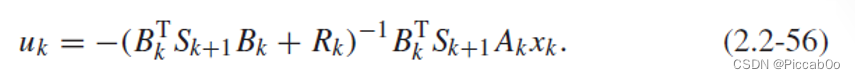
此处，控制量可以利用Kalman gain改写成：

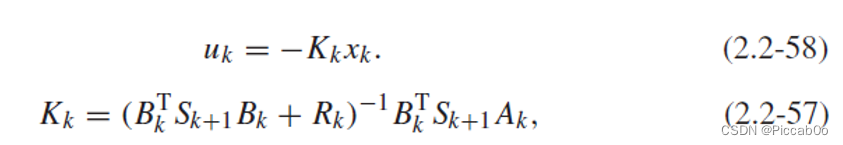
因此，为了找到最优控制量，只需要求解Riccati equation找到$S_k$，算出Kalman Gain即可。

同时，很有趣的一点是，最优控制序列$u_k$是状态$x_k$的比例函数。

（2.4-4）总结：

对于终端状态不确定的LQ问题，求解步骤总结如下：

对于the final-state weighting matrix $S_k$的原始形式，可以采用Kalman Gain改写：

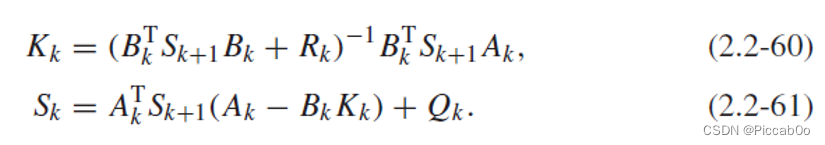
其等价于Joseph stabilized version of the Riccati equation：

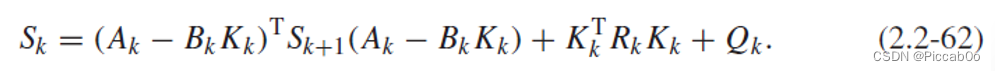
其求解起来具有更优的数值求解性能。

（2.4-5）对该情况下性能指标的研究：

研究上述最优控制量作用下系统的性能指标：

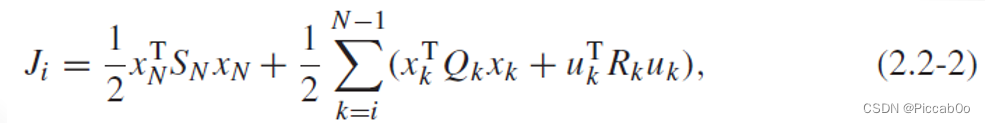
利用下式改写$J_i$：


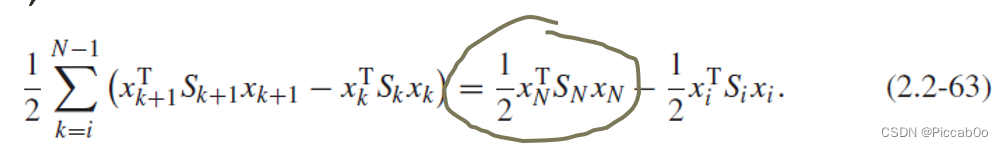
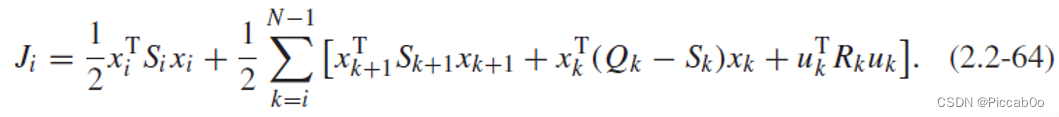
再将$x_{k+1}=A_k{x}_k+B_k{u}_k$代入，等价于：

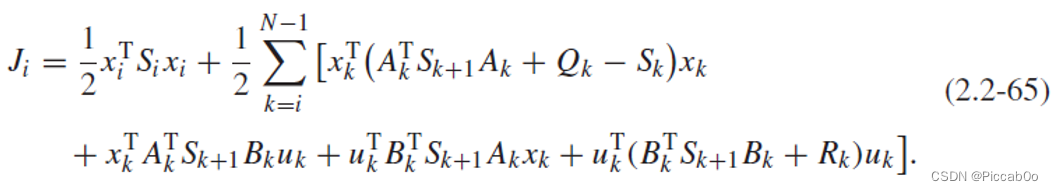
根据Riccatt Equation(2.2-53)，其又可以写成：

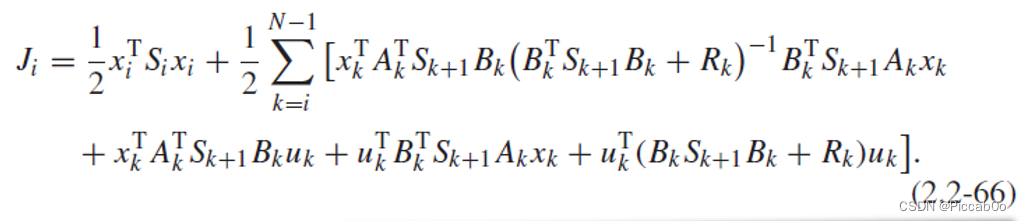
可以整理成：

容易发现，当采用最优控制量$u_k$控制时，性能指标为：

更一般地，$\forall k\in [i,N]$，都能算出$[k,N]$区间段的性能指标$J_k$：

由此，称$S_k$为performance index kernel matrix。

（2.4-6）与前述内容的联系

说明：

为了直观地理解基于Riccati方程的控制律，回顾前述内容。

在静态优化部分例1.2-2，考虑二次型性能指标：

其线性约束设为：

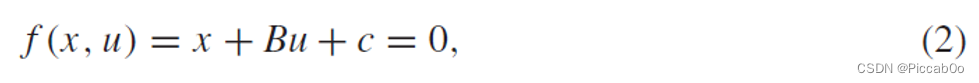
写出Hamilton函数：

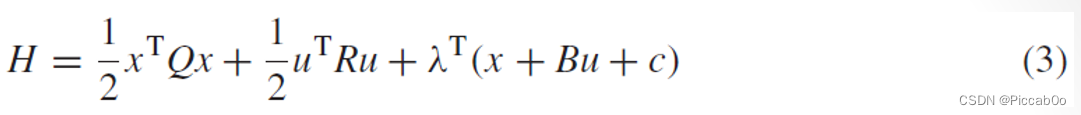
可以得出：

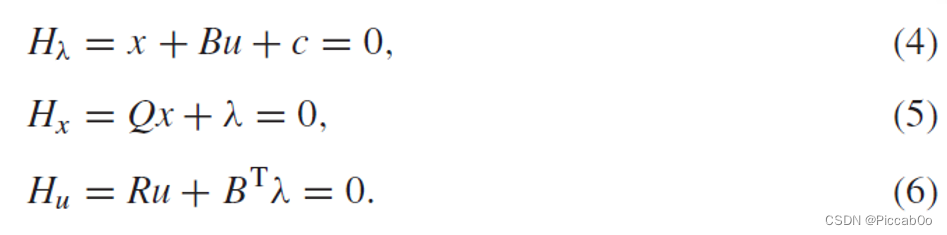
最优控制量：

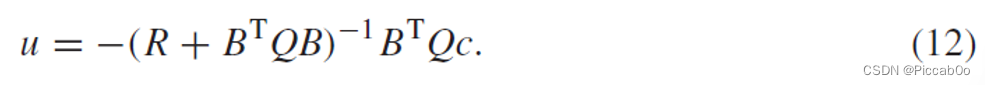
通过最优控制量，可以得到最优状态和拉格朗日乘子：

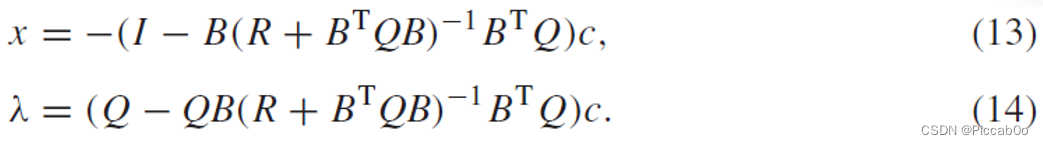
利用the matrix inversion lemma，拉格朗日乘子可以改写成：

利用式(1.2-31)：

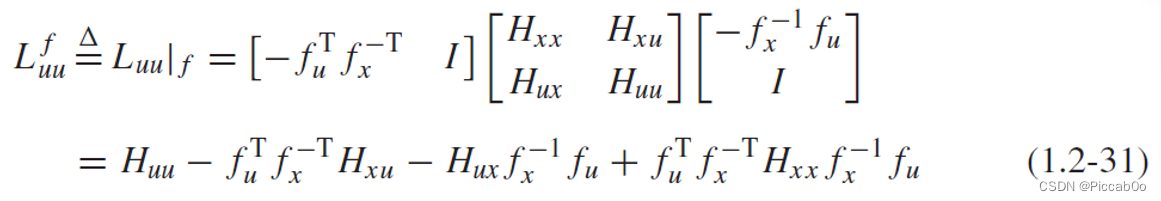
可以得出the constrained curvature matrix ：

回顾：

①由式(2.2-66)可得time-varying curvature matrix：

$\frac{{\partial }^2{J}_i}{\partial u_k^2}=B_k^T{S}_{k+1}{B}_k+R_k$

易知，时变情况下的系统与静态系统的曲率矩阵具有类似的形式。

②由式(2.2-51)经the matrix inversion lemma 改写可得状态表达式：

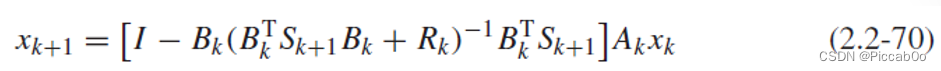
其也与静态系统的最优状态(13)具有类似的形式。

③在终端固定条件的讨论零输入情况下（$B_k=0$），二次的Riccati Eqution也降阶成了线性的Lyapunov equation：

（2.4-7）示例：

$Pag{e}_{158}-Pag{e}_{169}$，例子中的$S_k$差分方程难以求解，分别讨论了不同情况下的数值求解方法。