学习笔记 - 决策树

已于 2022-11-12 09:55:36 修改
阅读量1.2k 收藏
点赞数
分类专栏： 学习笔记 文章标签： 决策树 学习
于 2022-10-12 21:48:15 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_52167116/article/details/127290827
版权

10.12学习笔记 - 决策树

学习了分类和回归问题下的决策树模型，手写决策树结构

一、决策树处理分类问题 - 鸢尾花

1.数据处理&划分数据集

# 引入包

from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import DecisionTreeRegressor
from sklearn.tree import plot_tree

from sklearn.datasets import load_boston
from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

import numpy as np
from matplotlib import pyplot as plt

# 加载数据集
X, y = load_iris(return_X_y=True)

# 切分数据集
X_train, X_test, y_train, y_test =train_test_split(X,y,test_size=0.15,random_state=1)

# 构建分类模型
dtc = DecisionTreeClassifier(max_depth=2)
# 这里默认为gini，以下两种情况都会阐述

# 模型评估
score = dtc.score(X=X_test, y=y_test)
# output: 0.9565217391304348

# 绘制决策树
plot_tree(dtc)

在这里插入图片描述

2.计算信息熵&构建二叉树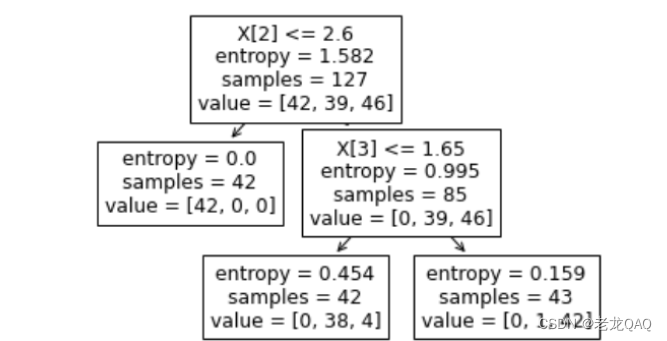在这里插入图片描述

上图为sklearn中plot_tree绘制出的决策树，DecisionTreeClassifier()参数为criterion="entropy"

根节点内容解释：

  • x[3] <= 0.8 以x的第三个特征是否小于0.8为判断标准
  • entropy —> 信息熵 —>代表信息混乱程度
  • samples = 127 ===》有127个样本
  • value = [42,39,46] 第一类有42个,第二类有39个…
"""
    计算训练集的熵

"""
samples = np.array([42, 39, 46])
p = samples / samples.sum()
entropy = -(p* np.log2(p)).sum()
entropy
# outputing: 1.5816621019614714


"""
遍历每个特征及其分割值
寻找下降最大的分割点

"""
X_train.shape
for feaure_idx in range(4):
    
    print("当前分割特征为", feaure_idx)
    
    for value in set(X_train[:, feaure_idx]):  # set 去重减少数据量
        print("分割值：", value)
        
        left_idx = X_train[:, feaure_idx] <= value
        right_idx = X_train[:, feaure_idx] > value
        
        X_left = X_train[left_idx]
        X_right = X_train[right_idx]
        
        print("向左走", X_left)
        print("向右走", X_right)
        
        break # 跳出当前循环
    
    break
  • 当数据量非常大、任务非常复杂时，观察内部细节可以通过break来打印第一个内(外）层循环
(1).计算信息熵

如何确定信息熵降低最快呢 —> 遍历每一个特征，比较遍历后的左右子树加权平均值

def get_entrepy(y):
    # 判断value如果是最大则没有右子树
    if len(y) == 0:
        return 0
    samples = np.array([y.tolist().count(idx) for idx in range(3)])
    p = samples /samples.sum() + 1e-6
    entropy = -(p * np.log2(p)).sum()
    return entropy

X_train.shape
for feaure_idx in range(4):

    print("当前分割特征为", feaure_idx)

    for value in set(X_train[:, feaure_idx]):  # set 去重减少数据量
        print("分割值：", value)

        left_idx = X_train[:, feaure_idx] <= value
        right_idx = X_train[:, feaure_idx] > value

        #求信息熵:计算每一类的概率，然后把每一类的概率相乘再相加再取负号

        # 求左边样本个数
        n_left = len(left_idx)
        n_right = len(right_idx)
        if n_left == 0 or n_right == 0:
            continue

        # 左
        X_left = X_train[left_idx]
        y_left = y_train[left_idx]

        # 左熵
        """
        print("左侧熵：", y_left)
        temp = {0:0, 1:0, 2:0} # 初始化一个temp 第0类为0个，第1类为0个，第2类为0个
        for ele in y_left: # 遍历，是哪一类哪一类就加1
            temp[ele] += 1
        print(temp)
         
        samples = list(temp.values())
        print(samples)
        
        """
        entropy_left = get_entrepy(y_left)
        print(entropy_left)

        # print([y_left.tolist().count(idx) for idx in range(3)])

        # 右
        X_right = X_train[right_idx]
        y_right = y_train[right_idx]

        # print("右侧熵", y_right)

        entropy_right = get_entrepy(y_right)
        print(entropy_right)

        # print("向左走", X_left)
        # print("向右走", X_right)

        # 加权平均
        entropy = n_left / (n_left + n_right) * entropy_left + n_right / (
            n_left + n_right) * entropy_right
        print(entropy)
            # 另一种写法
        print(np.average(a = np.array([entropy_left,entropy_right]),weights = np.array([n_left,n_right])))

        break

    break
"""output

当前分割特征为 0
分割值： 4.8
3.8420441376530785e-05
1.5562814756042398
0.7781599480228082
0.7781599480228082
"""

判断哪个熵减最大，思路是计算所有分出值的熵的最小值

#              特征编号       当前分割值           entropy      
best_split = {"feature_idx":0,"feature_value":0,"entropy":np.inf}

for feaure_idx in range(4):

    # print("当前分割特征为", feaure_idx)

    for value in set(X_train[:, feaure_idx]):  # set 去重减少数据量
        # print("分割值：", value)

        left_idx = X_train[:, feaure_idx] <= value
        right_idx = X_train[:, feaure_idx] > value

        #求信息熵:计算每一类的概率，然后把每一类的概率相乘再相加再取负号

        # 求左边样本个数 这里不能用len 因为right_idx里面是True和False，长度一样
        n_left = sum(left_idx)
        n_right = sum(right_idx)

        # 左
        X_left = X_train[left_idx]
        y_left = y_train[left_idx]

        # 左熵
        """
        print("左侧熵：", y_left)
        temp = {0:0, 1:0, 2:0} # 初始化一个temp 第0类为0个，第1类为0个，第2类为0个
        for ele in y_left: # 遍历，是哪一类哪一类就加1
            temp[ele] += 1
        print(temp)
         
        samples = list(temp.values())
        print(samples)
        
        """
        entropy_left = get_entrepy(y_left)
        # print(entropy_left)

        # print([y_left.tolist().count(idx) for idx in range(3)])

        # 右
        X_right = X_train[right_idx]
        y_right = y_train[right_idx]

        # print("右侧熵", y_right)

        entropy_right = get_entrepy(y_right)
        # print(entropy_right)

        # print("向左走", X_left)
        # print("向右走", X_right)

        # 加权平均
        entropy = n_left / (n_left + n_right) * entropy_left + n_right / (n_left + n_right) * entropy_right
        # print(entropy)
        # 另一种写法
        # print(np.average(a = np.array([entropy_left,entropy_right]),weights = np.array([n_left,n_right])))

        # 判断是否为最佳 - 野蛮计算 穷举思想
        if entropy < best_split["entropy"]:
            best_split["feature_idx"] = feaure_idx
            best_split['feature_value'] = value
            best_split["entropy"] = entropy

注意：np.inf 代表无穷大(infinity)

输出计算结果best_split：

best_split
# output:{'feature_idx': 2, 'feature_value': 1.9, 'entropy': 0.666038791145047}
  • 这里发现与sklearn中feature_value有差距，接着完善
values = list(set(X_train[:,2]))  # X_train[:,2]行都要第二列
values.sort()
values

在这里插入图片描述
上图为计算结果，可以发现这里遍历的是离散值，所以feature_value会从上面的数字中产生，而sklearn中将数据视为连续数据所以将 （1.9+3.3）/ 2 = 2.6 做为分割值，鲁棒性会更高

4.基尼系数

  • Q:为什么工程中都使用基尼系数呢？

    • 基尼系数 gini = P*(1-P)

    • entropy = -P(logP)
      (1-P)和(logP)都是大于零的减函数，从逻辑上讲都是一样的，但是(1-P)计算代价很低，所以不妨用(1-P)代替(logP)

在这里插入图片描述

(1).计算基尼系数
def get_gini(y):
    """
        根据标签，计算 gini 系数
    """
    
    samples = np.array([y.tolist().count(idx) for idx in range(3)])
    
    print(samples)
    p = samples / samples.sum()
    
    gini = (p * (1-p)).sum()
    
    return gini

二、回归问题 -波士顿房价预测

1.划分数据集

X,y = load_boston(return_X_y=True)

X_train, X_test, y_train, y_test =train_test_split(X,y,test_size=0.12,random_state=1)

dtr = DecisionTreeRegressor(max_depth=2)

dtr.fit(X=X_train,y=y_train)

plot_tree(dtr)

在这里插入图片描述
这里的value其实就是均值

y_train.mean()
# output:22.574831460674158
  • 回归问题怎么求信息熵 （一堆连续数据怎么衡量混乱程度 ） ==》方差
y_train.var()
# output:82.57397328620124

这里的mse是假mse 其实就是方差

"""
    穷举思想
    
    遍历每个特征及其分割值
    寻找方差下降最快的分割点

"""

#              特征编号       当前分割值           entropy      
best_split = {"feature_idx":0,"feature_value":0,"mse":np.inf}

for feaure_idx in range(13): # 13 个特征

    # print("当前分割特征为", feaure_idx)

    for value in set(X_train[:, feaure_idx]):  # set 去重减少数据量
        # print("分割值：", value)

        left_idx = X_train[:, feaure_idx] <= value
        right_idx = X_train[:, feaure_idx] > value

        #求信息熵:计算每一类的概率，然后把每一类的概率相乘再相加再取负号

        # 求左边样本个数 这里不能用len 因为right_idx里面是True和False，长度一样
        n_left = sum(left_idx)
        n_right = sum(right_idx)
        
        if n_right == 0:
            continue

        # 左
        X_left = X_train[left_idx]
        y_left = y_train[left_idx]

        # 左熵
        """
        print("左侧熵：", y_left)
        temp = {0:0, 1:0, 2:0} # 初始化一个temp 第0类为0个，第1类为0个，第2类为0个
        for ele in y_left: # 遍历，是哪一类哪一类就加1
            temp[ele] += 1
        print(temp)
         
        samples = list(temp.values())
        print(samples)
        
        """
        mse_left = y_left.var()
        # print(entropy_left)

        # print([y_left.tolist().count(idx) for idx in range(3)])

        # 右
        X_right = X_train[right_idx]
        y_right = y_train[right_idx]

        # print("右侧熵", y_right)

        mse_right = y_right.var()
        # print(entropy_right)

        # print("向左走", X_left)
        # print("向右走", X_right)

        # 加权平均
        mse = n_left / (n_left + n_right) * mse_left + n_right / (n_left + n_right) * mse_right
        # print(entropy)
        # 另一种写法
        # print(np.average(a = np.array([entropy_left,entropy_right]),weights = np.array([n_left,n_right])))

        # 判断是否为最佳 - 野蛮计算 穷举思想
        if mse < best_split["mse"]:
            best_split["feature_idx"] = feaure_idx
            best_split['feature_value'] = value
            best_split["mse"] = mse



best_split # 同理 （71+74） / 2 = 72.5
# output:{'feature_idx': 12, 'feature_value': 9.71, 'mse': 45.50584908896213}

查看feature_value

sorted(X_train[:,12])
怎么画出决策树-两种决策树的可视化方法
botf201802的博客
12-01 9176
策树模型是一种常用于研究类别归属和预测关系的模型。在决策树中，每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。
Python小白记录2：Decision Tree中tree.plot_tree参数解释
chanwoyee1的博客
10-25 7148
1.参考网站：sklearn.tree.plot_tree — scikit-learn 1.0 documentationhttps://scikit-learn.org/stable/modules/generated/sklearn.tree.plot_tree.html2. 中英文解释（自己 Parameters: 1. decision_tree:decision tree regressor or classifier #决策树 2. max_depth:int, default=No..
[机器学习&数据挖掘]机器学习实战决策树plotTree函数完全解析
tian544556的博客
09-26 1246
https://www.cnblogs.com/fantasy01/p/4595902.html
【scikit-learn】sklearn.tree.plot_tree() 函数：决策树可视化
最新发布
彬彬侠的博客
03-19 429
plot_tree()是sklearn.tree提供的决策树可视化工具，可以直观地查看决策规则、分裂特征、类别分布，适用于分类和回归任务的决策树模型。plot_tree()可视化决策树结构，适用于DecisionTreeClassifier和DecisionTreeRegressor，可以帮助理解模型决策逻辑，是调试和解释决策树的好工具。
【机器学习&数据挖掘】matplotlib画一棵决策树：plotTree函数完全解析
像我这样的人
03-15 2011
在看机器学习实战时候，到第三章的对决策树画图的时候，有一段递归函数怎么都看不懂，因为以后想选这个方向为自己的职业导向，抱着精看的态度，对这本树进行地毯式扫描，所以就没跳过，一直卡了一天多，才差不多搞懂，才对那个函数中的plotTree.xOff的取值，以及计算cntrPt的方法搞懂，相信也有人和我一样，希望能够相互交流。 先把代码贴在这里： import matplotlib.pyplot as ...
《机器学习实战》决策树plotTree函数完全解析
jiangsujiangjiang的博客
11-22 3069
函数中的plotTree.xOff的取值，以及计算cntrPt的方法 python3.X 环境下的代码 import matplotlib.pyplot as plt #这里是对绘制是图形属性的一些定义，可以不用管，主要是后面的算法 decisionNode = dict(boxstyle="sawtooth", fc="0.8") leafNode = dict(boxstyle="r...
决策树
酸乳乳酸的博客
06-06 321
决策树（Decision Tree）主要是用来处理分类问题，是最经常使用的数据挖掘算法之一。 决策树须知概念 熵指的是体系的混乱程度 信息熵（香农熵）是一种信息的度量方式，表示信息的混乱程度，信息越有序，熵越低。 信息增益：在划分数据集前后信息发生的变化称为信息增益 决策树工作原理： 决策树算法特点： 优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数...
tree.plot_tree（）函数里面具体的参数作用
qq_47104322的博客
06-27 1万+
课程设计的学习记录
《机器学习by周志华》学习笔记-决策树-01决策树流程与划分规则
vanilla698的博客
05-10 1099
本书中的「决策树」有时指学习方法，有时指学得的树。
《机器学习by周志华》学习笔记-决策树-04多变量决策树
vanilla698的博客
08-14 1230
我们将每个样本的属性作为坐标轴，则n个属性的描述值的样本就对应了n维空间中的一个数据点。对样本分类就意味着我们将在这个空间中寻找不同类样本之间的分类边界。多变量决策树，亦称「斜决策树(obliquedecision tree)」即决策树的分类边界由若干与属性轴平行的分段组成。
《机器学习by周志华》学习笔记-决策树-03连续值与缺失值
vanilla698的博客
08-12 1045
到目前为止，我们在决策树01、02中仅讨论了基于离散属性来生成决策树，而现实任务中常会遇到连续属性，所以在本章的学习中，我们将会讨论如何在决策树学习中使用连续属性。缺失值处理现实生活中的数据结构经常会遇到不完整的样本，即有些样本的某些属性值缺失。且样本数量越大，缺失的属性值会越多。例如医疗数据中隐私测量结果等。
《机器学习by周志华》学习笔记-决策树-02预剪枝与后剪枝
vanilla698的博客
08-05 1117
上文「」的学习中，我们了解了著名的3种决策树算法ID3、C4.5、CART。这3种决策树算法最根本的核心就是根据特征选择离散属性作为节点来搭建树结构，运用搭好的结构进行推理。剪枝(pruning)则就是将搭好的决策树去掉一些「非叶节点」的过程。
分类问题学习笔记-决策树
Pioo_的博客
11-16 1073
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录决策树案例:原理：基于信息论的三种决策树算法：1、ID3算法**信息熵:****案例：**ID3算法的不足2、C4.5算法3、CART算法优点：缺点：关于剪枝：python鸢尾花案例： 决策树 案例: 假如现在我想买一个西瓜，需要判断好瓜，还是坏瓜。西瓜拿过来后先看纹理，纹理如果不清晰直接pass，纹理清晰的再看根蒂，触感等其他特征，如果我此时构建了一颗决策树，没问题，马上就可以知道是好瓜，还是坏瓜，如下图所示： 原理： 决策树
机器学习实战决策树plotTree函数完全解析
乐乐的博客
06-22 1万+
原文  http://www.cnblogs.com/fantasy01/p/4595902.html 在看机器学习实战时候，到第三章的对决策树画图的时候，有一段递归函数怎么都看不懂，因为以后想选这个方向为自己的职业导向，抱着精看的态度，对这本树进行地毯式扫描，所以就没跳过，一直卡了一天多，才差不多搞懂，才对那个函数中的plotTree.xOff的取值，以及计算cntrPt的方法
决策树(Decision Tree) | 绘制决策树
热门推荐
Data Hero
09-22 1万+
01 起 在这篇文章中，我们讲解了如何训练决策树，然后我们得到了一个字典嵌套格式的决策树结果，这个结果不太直观，不能一眼看着这颗“树”的形状、分支、属性值等，怎么办呢？ 本文就上文得到的决策树，给出决策树绘制函数，让我们对我们训练出的决策树一目了然。 在绘制决策树之后，我们会给出决策树的使用方法：如何利用训练好的决策树，预测训练数据的类别？ 提示：不论是绘制还是使用决策树，中心思想都是递归。 ...
机器学习（二）——决策树（DecisionTree）
qq_40296818的博客
02-01 794
机器学习（一）——决策树（DecisionTree）一、算法简介1.1 概念1.2 决策树基本构造步骤1.2.1 特征选择 一、算法简介 1.1 概念 决策树（Dicision Tree）是一种基本的分类与回归方法。决策树模型是一种描述对实例进行分类的树形结构。决策树由结点（node）和有向边（directed edge）组成。结点由两种类型：内部结点（internal node）和叶节点（leaf node）。内部结点表示一个特征或属性，叶节点表示一个类。 1.2 决策树基本构造步骤 一般分三步： 特征
机器学习--决策树（第六章）
qq_52754254的博客
05-23 1971
决策树 决策树.py from sklearn.tree import DecisionTreeClassifier #创建分类器对象 tree=DecisionTreeClassifier(criterion="entropy") #训练数据fit tree.fit([[0],[1],[2],[3]],["a","a","b","c"]) #预测新数据 target=tree.predict([[2]]) #模型评估，打分，验证方法，评估方式 print(target) print(tree.scor
decision tree
weixin_44412864的博客
04-21 191
参考： 决策树：https://github.com/apachecn/AiLearning/blob/master/src/py3.x/ml/3.DecisionTree/DecisionTree.py 画图： https://github.com/apachecn/AiLearning/blob/master/src/py3.x/ml/3.DecisionTree/decisionTreePlot.py 文档： https://apachecn.gitee.io/ailearning/#/docs/ml
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值