「1066」Root of AVL Tree-CSDN博客

本文链接：https://blog.csdn.net/weixin_52435933/article/details/128291022

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

Ω

AVL，平衡二叉搜索树，不仅拥有BST的性质，同时每个顶点左右两棵子树的高度差不超过1，从而使树的高度尽可能维持在一个较低水平，提高搜索效率。给出一组数据，输出最终AVL的根节点，注意每个元素插入后都应及时调整为AVL。

当初看树这一块的时候，AVL的旋转调整让我头疼不已，现在亦是如此。苦苦思索，原来这是第一次撞上AVL的题目，于是我又回去重温了一遍《数据结构与算法分析》里的相关内容。

每次插入一个数后我们都从该树开始向根节点回溯，找到第一个左右子树高度差>1的节点X，只要将这棵子树恢复至插入前的高度即可重新满足AVL。

接下来我们将插入后不满足平衡性的情形分为两种(每种都包含两个镜像对称的情况)：

向X节点的左(右)子节点的左(右)子树插入后不满足
向X节点的左(右)子节点的右(左)子树插入后不满足

我们用来表示子树，来表示子树的高度，首先显然

那么不可能是空树，因为。因此我们还可以将进行拆分：

其次，否则在插入之前就已经不满足平衡性，另外由于节点X是第一个不满足平衡性的节点，因此。

综上所述，，且。

接下来，我们通过两种不同的旋转方法在不破环BST的前提下使其重新符合平衡性(序号与上述情形相对应，只考虑镜像对称中的一种情况)：

拎住绿点向上提，成为节点X的左子树

显然满足平衡性，且BST的有序性也未被破坏
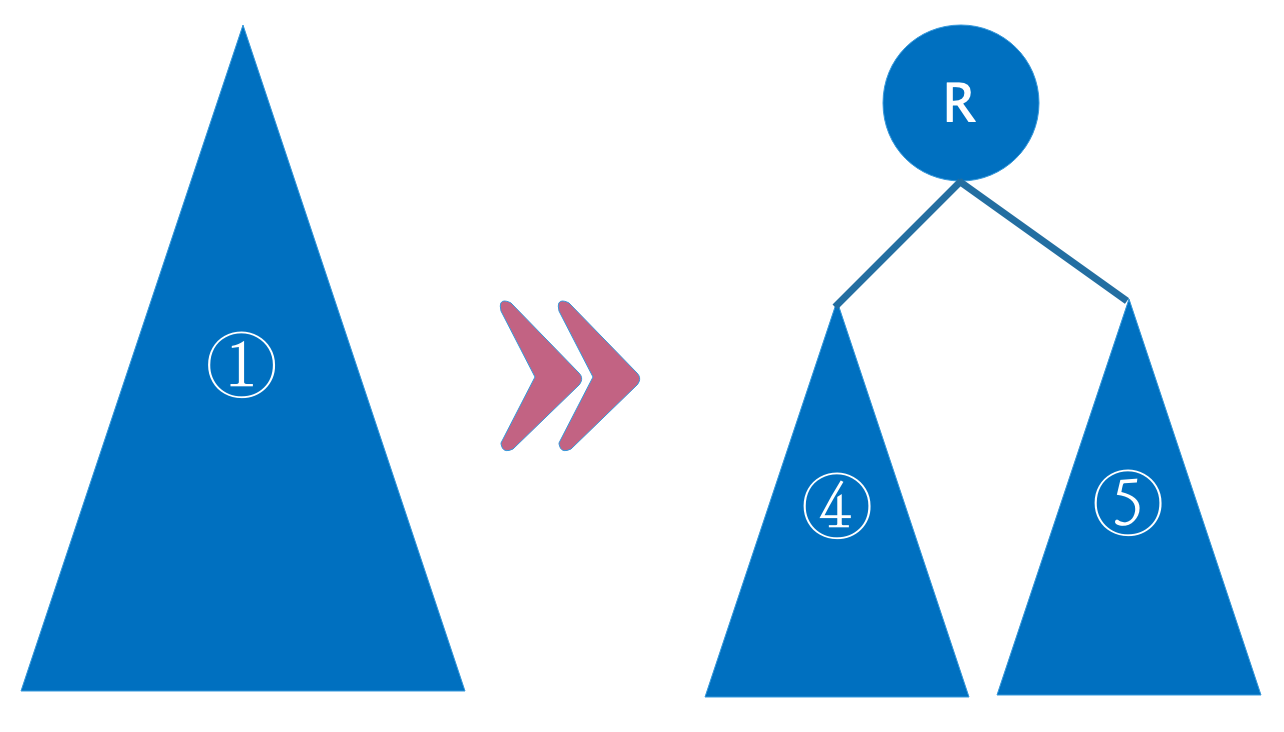
拎住节点R向上提成为根节点，想象每条边的端点都是有磁性的，在上提的过程中脱落自动吸附到其他节点上，绿节点和节点X成为其左右子树，而成为绿节点的右子树，成为X节点的左子树

和的高度关系无法确定，但注意到，因此依然可以肯定是符合平衡性要求的。

🐎

#include <iostream>
#include <map>
#include <vector>
#define diff(x) height[child[x].first]-height[child[x].second]
using namespace std;

map<int, pair<int, int>> child;
map<int, int> height;

int insert(int &node, int &num)
{
    if (node == -1)
    {
        node = num;
        height[num] = 1;
        child[num] = pair(-1, -1);
        return num;
    }
    if (num > node)
        child[node].second = insert(child[node].second, num);
    else
        child[node].first = insert(child[node].first, num);
    height[node] = max(height[child[node].first], height[child[node].second]) + 1;
    int head = node;
    if (abs(diff(node)) > 1)
    {
        bool isLeft = diff(node) > 0;
        int &inSon = isLeft ? child[node].second : child[node].first,
            &outSon = isLeft ? child[node].first : child[node].second,
            &inGson = isLeft ? child[outSon].second : child[outSon].first,
            &outGson = isLeft ? child[outSon].first : child[outSon].second;
        if ((diff(node) ^ diff(outSon)) > 0)
        {
            height[node] = max(height[inSon], height[inGson]) + 1;
            height[outSon] = max(height[node], height[outGson]) + 1;
            head = outSon;
            outSon = inGson;
            inGson = node;
        }
        else
        {
            int &inGGson = isLeft ? child[inGson].second : child[inGson].first,
                &outGGson = isLeft ? child[inGson].first : child[inGson].second;
            height[outSon] = max(height[outGson], height[outGGson]) + 1;
            height[node] = max(height[inSon], height[inGGson]) + 1;
            height[inGson] = max(height[node], height[outSon]) + 1;
            head = inGson;
            inGson = outGGson;
            outGGson = outSon;
            outSon = inGGson;
            inGGson = node;
        }
    }
    return head;
}

int main()
{
    int n, head, m;
    cin >> n >> head;
    child[head] = pair(-1, -1);
    height[head] = 1;
    for (int i = 1; i < n; ++i)
    {
        cin >> m;
        head = insert(head, m);
    }
    cout << head;
}