C++简单实现Bézier曲线

贝塞尔曲线有着很多特殊的性质在图形设计和路径规划中应用都非常广泛。贝塞尔曲线完全由其控制点决定其形状，n个控制点对应着n-1阶的贝塞尔曲线，并且可以通过递归来定义。本篇文章的重点在于对Bézier Curve的理解以及用OpenGL绘制Bézier Curve。

〄 Bézier Curve·1阶

给定两个已知坐标的控制点P0，P1，那么1阶贝塞尔曲线可以用一个关于t的参数方程来描述：

很显然，这表示的即是两控制点之间的线段，而每一个则表示线段上的一个点，这个关于的动点我们姑且先称之为贝塞尔动点，贝塞尔动点遍历便构成贝塞尔曲线。

⚠️事实上贝塞尔曲线本身跟t是无关的，t只是方便描述曲线上的点而存在的，可以认为是画出贝塞尔曲线的画笔。

〄 Bézier Curve·2阶

给定三个已知坐标的控制点P0，P1，P2，那么这时候有两个线段，我们可以先求出这两个线段上的贝塞尔动点P0',P1'，然后求两个贝塞尔动点线段上的贝塞尔动点(三个贝塞尔动点关联同一个t)，第三个贝塞尔动点将构成2阶贝塞尔曲线：

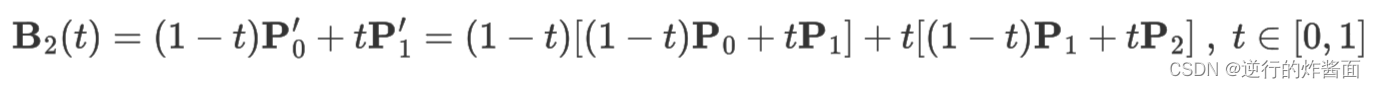
那么2阶贝塞尔曲线的参数方程即为

我们可以看到这是一个递归的过程。

〄 Bézier Curve·3阶

同理3阶贝塞尔曲线的方程为

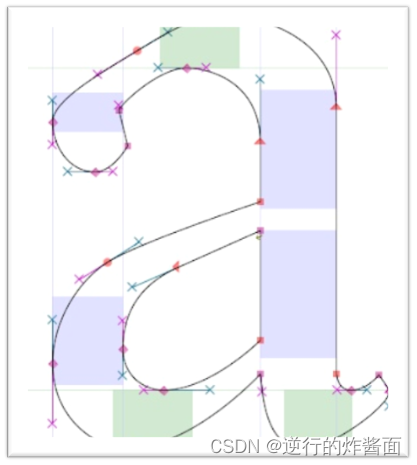
下图是当时的贝塞尔动点线段以及相应的3阶贝塞尔曲线

事实上对于贝塞尔曲线参数方程中每个控制点前的系数都是一个关于的函数，而这些系数函数我们可以类比杨辉三角(贝塞尔曲线的递归过程本质上就是个杨辉三角)

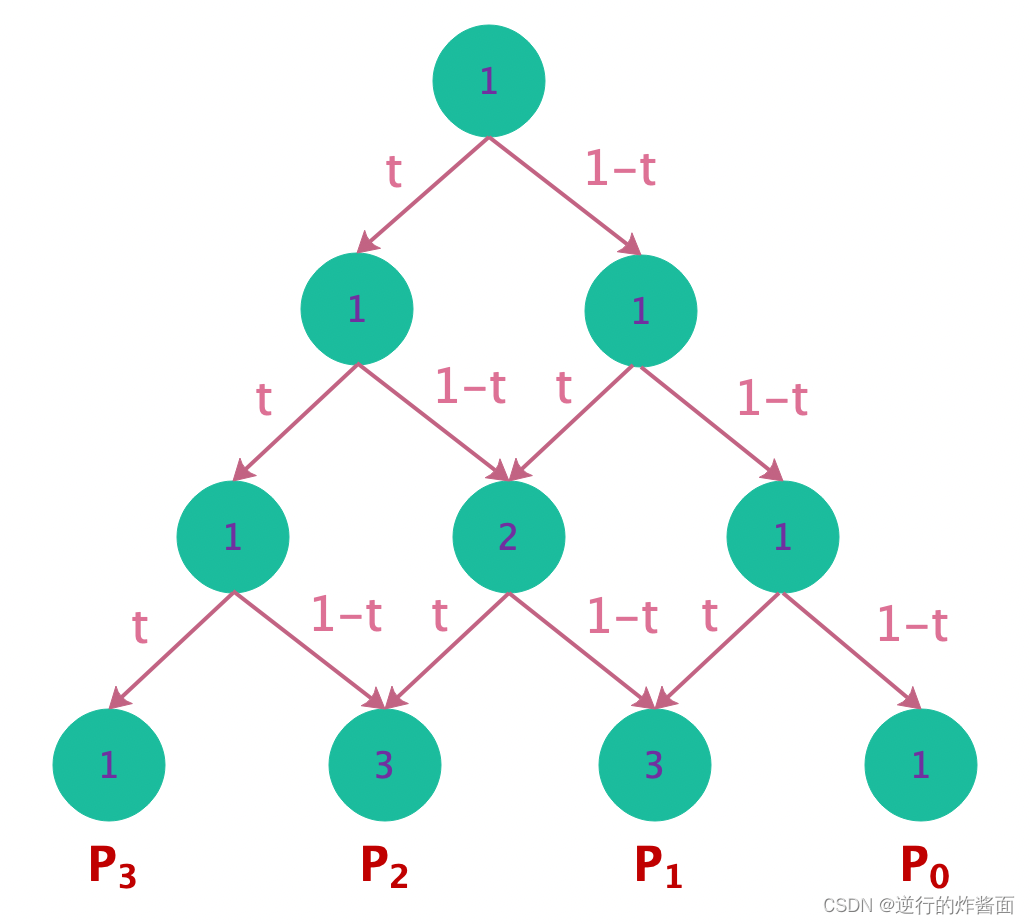
上图只是一个三阶的杨辉三角，我们可以看到每个控制点所在的叶子节点到根结点(最上面的那个点)的路径乘积乘以其所在叶子节点上的数字即为其系数函数。比如说P2，我们随便取一条到根结点的路径(不管哪条路径，乘积都是一样的)，将路径上的表达式进行相乘得到，再乘以其叶子节点3得到，对照B3(t)即为P2的系数。

〄 Bézier Curve· n阶

注意到上图中的杨辉三角其实就是的展开式，因此我们其实可以直接写出n阶贝塞尔曲线Bn(t)中控制点Pi(0 ≤ i < n)的系数为

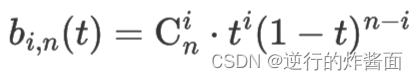
上式又称为n阶的波恩斯坦基底多项式。

---

接下来就到了激动人心的绘制阶段。不过其实理论内容已经差不多了，剩余的只是C++编程，OpenGL运用。

代码里没有什么高深的思想，没有啥优化(概括：懒)，就是实现了一个点类，然后不断递归求出新的控制点坐标。当然OpenGL不能绘制连续的曲线，因此我们需要化曲为直。这时候就派上用场了，我将从中均匀地取100个出来分别绘制相应的点，最后将这些点连起来即可。

⚡︎ 算法说明

1. 实现了一个点类Point，用于存储一个点的坐标(double x,y)，并重载了*、+符号，使坐标可以直接与浮点数进行加乘运算

2. 首先需要用户输入需要绘制的贝塞尔曲线的阶数n，随后输入(n+1)个控制定点的坐标，最后指定t0来绘制出相应的中间迭代控制点

   

3. 对每个点的坐标都/100来满足实际绘图坐标的范围(绘制函数传入的坐标范围)

4. vector<vector<Point>> control_points存储参数所对应的每一次迭代的控制点坐标，control_points[i]存储的是第次迭代的控制点坐标

5. 若表示第i次迭代的第j个控制点，那么控制点的迭代公式：

   

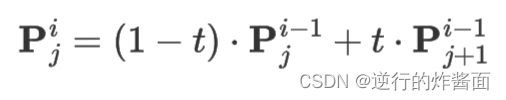
6.  绘制贝塞尔曲线是化曲为直，首先均匀取了100个，画出每个t所对应的位于贝塞尔曲线上的点，最后将每个点连起来
7. vector<vector<Point>> middle_points存储的是每个t迭代过程中的中间控制点坐标以及最后所要连起来的100个点
8. 绘制过程：t0对应的迭代过程控制点连线→贝塞尔曲线连线→t0在贝塞尔曲线上对应的点

其余就看代码注释吧～

---

C☺DE

#include <glew.h>
#include <glfw3.h>
#include <vector>
#include <iostream>

using namespace std;

//重载了*，+运算符的点类
class Point
{
public:
    double x, y;

    Point(double _x, double _y) : x(_x), y(_y) {};

    inline Point operator*(const double &t) const
    {
        return Point(t * this->x, t * this->y);
    }

    inline Point operator+(const Point &rhs) const
    {
        return Point(this->x + rhs.x, this->y + rhs.y);
    }
};

int main(void)
{
    int n;
    cout << "Bézier Curve的阶数：";
    cin >> n;

    //control_points存储指定t的每一次迭代控制点，middle_points存储绘制过程中的每一次迭代控制点(t会变)
    vector<vector<Point>> control_points(n + 1), middle_points(n + 1);
    double x, y, t0;
    cout << "请输入" << n + 1 << "个控制点坐标(0 ≤ |x|,|y| ≤ 100)：" << endl;
    for (int i = 0; i < n + 1; ++i)
    {
        cin >> x >> y;
        control_points[0].emplace_back(Point(x / 100, y / 100));
    }

    //输入指定t，可绘制出t0时每一次的迭代控制点
    cout << "t0 = ";
    cin >> t0;
    //计算t0时每一次的迭代控制点
    for (int i = 1; i < n + 1; ++i)
        for (int j = 0; j < n + 1 - i; ++j)
            control_points[i].emplace_back(control_points[i - 1][j] * (1 - t0) + control_points[i - 1][j + 1] * t0);
    //求100个t所对应的点
    middle_points[0] = control_points[0];
    for (int k = 0; k < 101; ++k)
    {
        double t = k / 100.0;
        for (int i = 1; i < n; ++i)
        {
            middle_points[i].clear();
            for (int j = 0; j < n + 1 - i; ++j)
                middle_points[i].emplace_back(middle_points[i - 1][j] * (1 - t) + middle_points[i - 1][j + 1] * t);
        }
        middle_points[n].emplace_back(middle_points[n - 1][0] * (1 - t) + middle_points[n - 1][1] * t);
    }
    //开始绘制，初始化glfw库
    if (!glfwInit())
        return -1;
    //创建窗口以及上下文
    GLFWwindow *window = glfwCreateWindow(800, 600, "Bézier Curve", NULL, NULL);
    if (!window)
        glfwTerminate();
    //建立当前窗口的上下文
    glfwMakeContextCurrent(window);
    //循环绘制使其停留在屏幕上
    while (!glfwWindowShouldClose(window))
    {
        glfwPollEvents();
        //背景颜色
        glClearColor(0.2, 0.1, 0.2, 1);
        glClear(GL_COLOR_BUFFER_BIT);

        //绘制t0时每次迭代的控制点连线
        glLineWidth(5);
        for (int i = 0; i < n; ++i)
        {
            //使每次迭代的控制点连线颜色不同
            glColor3f(1.0 * (n - 1 - i) / (n - 1), 1.0 * i / (n - 1), 0);
            glBegin(GL_LINE_STRIP);
            for (auto &p: control_points[i])
                glVertex2f(p.x, p.y);
            glEnd();
        }
        //绘制贝塞尔曲线
        glColor3f(0, 0, 1);
        glBegin(GL_LINE_STRIP);
        for (auto &p: middle_points[n])
            glVertex2f(p.x, p.y);
        glEnd();

        //绘制出贝塞尔曲线上t0所对应的点
        glColor3f(0, 0.7, 0.7);
        glPointSize(20);
        glEnable(GL_POINT_SMOOTH);
        glBegin(GL_POINTS);
        glVertex2f(control_points[n][0].x, control_points[n][0].y);
        glEnd();

        glfwSwapBuffers(window);
    }
    glfwTerminate();
    return 0;
}

---

⚛︎ 5 order Bezier curve (t0=0.5)