多元回归分析

Fran OvO

已于 2022-12-21 21:59:09 修改

阅读量6.8k

点赞数 12

分类专栏：数学建模文章标签：回归逻辑回归

于 2022-12-12 12:58:29 首次发布

本文链接：https://blog.csdn.net/weixin_52640021/article/details/128268511

版权

数学建模专栏收录该内容

9 篇文章 5 订阅

订阅专栏

建模复习

前言

回归分析是数据分析中最基础也是最重要的分析工具。通过研究自变量X和因变量Y的相关关系，尝试去解释Y的形成机制，进而达到通过X去预测Y的目的。

常见的回归分析有：线性回归，0-1回归，定序回归，计数回归和生存回归。其划分的依据是因变量Y的类型。

一、回归的思想

1,介绍

回归分析：研究X和Y之间的相关性。

2，回归分析的分类

类别	模型	Y	例子
线性回归	OLS,GLS(最小二乘)	连续数值型变量	GDP与产量，收入关系
0-1回归	logistic回归	二值变量（0-1）	是否好瓜，是否突变
定序回归	probit回归	定序变量	等级评定（优良差）
计数回归	泊松分布	计数变量	每分钟的车流量
生存回归	cox等比例风险回归	生存变量（截断数据）	企业产品寿命

3，数据类型

数据类型	建模方法
横截面数据：某一时间点收集的不同对象数据	多元回归分析
时序数据：一串时间序列数据	LSTM,灰色时间预测，指数平滑，ARIMA,SARIAM,GARCH,VAR,协积
面板数据：横截数据+时序数据	固定效应，随机效应，静态面板，动态面板

横截数据在比赛中，往往可以使用回归进行建模，建立自变量和因变量间的相关分析模型和预测模型

二、一元线性回归

1，一元线性函数拟合

设这些样本点为 $\left ( x_{i},y_{i} \right ),i=1,2,...,n$

我们设置拟合曲线为 $y=kx+b$ ,令拟合值 $\hat{y}_{i}=k x_{i}+b$

那么 $\hat{k}, \hat{b}=\underset{k, b}{\arg \min }\left(\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\right)=\underset{k, b}{\arg \min }\left(\sum_{i=1}^{n}\left(y_{i}-k x_{i}-b\right)^{2}\right)$

令 $L=\sum_{i=1}^{n}\left(y_{i}-k x_{i}-b\right)^{2}$ ，现在找k和b,使得L最小。

（L为损失函数，在回归中也叫作误差平方和）

2，一元线性回归模型

假设x是自变量，y是因变量，且满足如下线性关系：

$y_{i} = \beta_{0}+\beta_{1} x_{i}+\mu_{i}$

$\beta_{0}$ ， $\beta_{1}$ 是回归系数， $\mu_{i}$ 为无法观测得且满足一定条件得扰动项

令预测值 $\widehat{y_{i}}=\widehat{\beta_{0}}+\widehat{\beta_{1}} x_{i}$ ，其中： $\begin{array}{c} \widehat{\beta_{0}}, \widehat{\beta_{1}}=\underset{\beta_{0}, \beta_{1}}{\operatorname{argmin}}\left(\sum_{i=1}^{n}\left(y_{i}-\widehat{y_{i}}\right)^{2}\right)=\underset{\beta_{0}, \beta_{1}}{\arg \min }\left(\sum_{i=1}^{n}\left(y_{i}-\widehat{\beta_{0}}-\widehat{\beta}_{1} x_{i}\right)^{2}\right) \\ \widehat{\beta_{0}}, \widehat{\beta_{1}}=\underset{i=1}{\arg \min }\left(\sum_{i=1}^{n}\left(\widehat{\mu_{i}}\right)^{2}\right) \end{array}$

我们称 $\widehat{\mu_{i}}=y_{i}-\widehat{\beta_{0}}-\widehat{\beta_{1}} x_{i}$ 为残差

这部分为建模凑字数部分（建模论文写作公式存储）

2.线性的理解

假设x是自变量，有是因变量，且满足如下线性关系：

$y_{i} = \beta_{0}+\beta_{1} x_{i}+\mu_{i}$

当然，线性假定并不是要求初始模型都呈现严格的线性关系。自变量与自变量可以通过变量替换转化成线性模型，如：

$\begin{array}{c} y_{i}=\beta_{0}+\beta_{1} \ln x_{i}+\mu_{i} \\ \ln y_{i}=\beta_{0}+\beta_{1} \ln x_{i}+\mu_{i} \\ y_{i}=\beta_{0}+\beta_{1} x_{i}+\beta_{2} x_{i}^{2}+\mu_{i} \\ y_{i}=\beta_{0}+\beta_{1} x_{1 i}+\beta_{2} x_{2 i}+\delta x_{1 i} x_{2 i}+\mu_{i} \end{array}$

对变量x进行ln操作，或平法，开方操作是提高模型准确性的一大常用数据预处理，当然，也容易出现过拟合。。。

3，回归系数

1，回归系数的解释

$y_{i} = \beta_{0}+\beta_{1} x_{i}+\mu_{i}$ ， $\beta_{0}$ ， $\beta_{1}$ 是回归系数

假设x为某产品品质评分(1-10之间)，y为该产品的销量，我们对和y使用一元线性回归模型,如果得到 $y=3.4+2.3x_{i}$ ;

评估分析：
3.4:在评分为0时，该产品的平均销量为3.4
2.3:评分每增加一个单位，该产品的平均销量增加2.3

2，内生性

(写建模论文严谨的解释)

内生性问题 (endogeneity issue) 是指模型中的一个或多个解释变量与误差项存在相关关系。换言之，如果 OLS回归模型中出现，则模型存在内生性问题，以致于 OLS 估计量不再是一致估计。

接上个假设，假设 $x_{1}$ 为某产品品质评分(1-10之间)， $x_{2 }$ 某产品价格， $y$ 为该产品的销量。那么我们建立多元线性回归模型 $y_{i} = \beta_{0}+\beta_{1} x_{2}+\beta_{2} x_{2}+\mu_{i}$

得到 $y_{i} =5.3+0.19 x_{1}-1.74x_{2}$

评估分析：

5.3:在评分为0日价格为0时，该产品的平均销量为5.3个(没现实意义)

0.19:在保持其他变量不变的情况下，评分每增加一个单位，该产品的平均销量增加0.19

-1.74:在保持其他变量不变的情况下，价格每增加一个单位，该产品的平均销量减少1.74

看见，加入新的自变量价格后，对回归系数的影响非常大，可能原因是产品评分和价格两变量存在相关性，所以遗漏变量导致的内生性问题

3，完全多重共线性

共线性问题指的是输入的自变量之间存在较高的线性相关度。共线性问题会导致回归模型
的稳定性和准确性大大降低，另外，过多无关的维度计算也很浪费时间。

计算VIT

解决法子：

1）向前逐步回归：将自变量逐个引入模型，每引入一个自变量后都要进行检验，显著时才加入回归模型。（缺点，随着以后其他自变量的引入，原来显著的自变量也可能变成不显著的了）

2）向后逐步回归：与向前逐步回归相反，先将所有变量均放入模型，之后尝试将其中一个自变量从模型中剔除，看整个模型解释因变量的变异是否有显著变化，之后将最没有解释力的那个自变量剔除；此过程不断迭代，直到没有自变量符合剔除的条件。（缺点：一开始把全部变量都引入回归方程，这样计算量比较大。若对一些不重要的变量，一开始就不引入，这样就可以减少一些计算。当然这个缺点随着现在计算机的能力的提升，已经变得不算问题了）

3）岭回归和lasso回归：正则化，这两种方法在OLS回归模型的损失函数上加入了不同的惩罚项，该惩罚项由回归系数的函数构成，一方面，加入的惩罚项能够识别出模型中不重要的变量，对模型起到简化作用，可以看作逐步回归法的升级版；另一方面，加入的惩罚项能够让模型变得可估计，即使之前的数据不满足列满秩。

4）改变特征（变量）的表现形式：有些变量可以改变其表现形式，如像网页的浏览次数、点击次数等特征属于长尾分布，可以对其进行log变换，变换后的变量可以有效的降低变量之间的相关性。

5）主成分分析（PCA）：通过主成分分析提取主要的特征，从而忽略次要的成分，得到相关性很低的特征。

4，拟合优度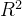 $R^{2}$

拟合优度（Goodness of Fit）是指回归直线对观测值的拟合程度。度量拟合优度的统计量是可决系数（亦称确定系数）R²。

R² 最大值为 1。R² 的值越接近1，说明回归直线对观测值的拟合程度越好；
反之，R² 的值越小，说明回归直线对观测值的拟合程度越差。

1 ）回归分为解释型回归和预测型回归。

预测型回归一般才会更看重 $R^{2}$ 。

2 ）可以对模型进行调整，例如对数据取对数或者平方后再进行回归。

3 ）数据中可能有存在异常值或者数据的分布极度不均匀。

$\begin{array}{c} R^{2}=\frac{\sum\left(\hat{y}_{i}-\bar{y}\right)^{2}}{\sum\left(y_{i}-\bar{y}\right)^{2}}=1-\frac{S S E}{S S T}=1-\frac{\sum\left(\hat{y}_{i}-y_{i}\right)^{2}}{\sum\left(y_{i}-\bar{y}\right)^{2}} \end{array}$

三，实验

1，变量说明

符号	解释
$\beta _{i}$	未知待估计参数
$\mu _{i}$	满足一定条件的误差项
VIF	方差膨胀因子
X	原始数据矩阵

2，模型的建立与求解

2.1，数据来源：

diabetes 是一个关于糖尿病的数据集，该数据集包括442个病人的生理数据及一年以后的病情发展情况。

from sklearn.datasets import load_iris, load_wine, load_diabetes

diabetes = load_diabetes()
data = diabetes['data']
target = diabetes['target']
feature_names = diabetes['feature_names']
df = pd.DataFrame(data, columns=feature_names)
df.head()  # 查看前几行数据

该数据集共442条信息，特征值总共10项, 如下:
age:年龄
sex:性别

bmi(body mass index):身体质量指数，是衡量是否肥胖和标准体重的重要指标，理想BMI(18.5~23.9) = 体重(单位Kg) ÷ 身高的平方
(单位m) bp(blood pressure):血压（平均血压）
s1,s2,s3,s4,s4,s6:六种血清的化验数据，是血液中各种疾病级数指针的6的属性值。 s1——tc，T细胞（一种白细胞）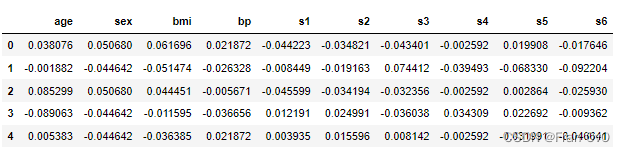

2.2，线性假设

已知442个病人的生理数据与年龄，性别，身体质量指数，BMI，六种血清的化验数据，有关。为了方便探求病人的生理数据与各项生理指标的具体关系，假设病人的生理数据（因变量）与各项生理指标（自变量）间的关系为线性关系：

$\begin{array}{c} y_{i}=\beta_{1} x_{i 1}+\beta_{2} x_{i 2}+\beta_{3} x_{i 3}+ \cdots+\beta_{10} x_{i 10}+\mu_{i}(i=0,1, \cdots, 442) \end{array}$

其中， $\beta _{i}$ 是未知代估参数， $\mu _{i}$ 是无法观测且满足一定条件的误差项

2.3，相关性分析（建模考虑点）

import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(15,8))
mask = np.triu(np.ones_like(df.corr(), dtype=bool))
sns.heatmap(df.corr(), annot=True, mask=mask, vmin=-1, vmax=1)
plt.title('Correlation Coefficient Of Predictors')
plt.show()

2.4，完全多重共线性（建模考虑点）

如果数据矩阵X不满秩，即存在某一解释变量可以被其他解释变量线性表示出，则存在“严格多重共线性”。其表现为： $\left ( X^{T}X^{-1} \right )$ 不存在，总体参数 $\beta$ 不可识别，无法定义最小二乘估计量。

严格多重共线性在现实数据中极少出现,现实中较为常见的是近似(非严格)多重共线性。其具体表现为: 存在第k个解释变量，如果将 $x_k$ 对其他解释变量 $\left \{ x_1,\cdots,x_{k-1},x_{k},\cdots,x_K \right \}$ 了进行回归，所得到的可决系数 $R^2$ 较高。在存在近似多重共线性的情况下，OSL 依然是最佳线性无偏估计，但不意味着 OSL 估计量方差绝对小。其主要负面效果为:单个系数的t检验不显著，或系数估计值不合理，甚至符号与理论值相反，另一种可能情况是增减解释变量会使得系数估计值发生很大的变化。直观来看，若两个(或多个)解释变量高度相关，则不容易区分它们对被解释变量的单独影响力。

2.5，运用VIF法检验多重共线性（建模考虑点）

VIF 全称为方差膨胀因子(Variance Inflation Factor)，其计算方法为:

假设共有k个自变量，则第m个自变量的 $VIF_{m}=1 /\left(1-R_{1 \sim k/m}^{2}\right)$ 。其中 $R_{1 \sim k/m}^{2}$ 是将第m个自变量作为因变量,对剩下的K-1个自变量回归得到的拟合优度。VIF越大说明第m个自变量与其他自变量的相关性越大。
定义回归模型的 $VIF=max\left \{ x_1,x_2,\cdots,x_K \right \}$ 。

一个经验规则是：若VIF >10，则认为该回归方程存在严重的多重共线性

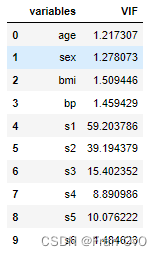
可以看出s1=59.203>10,s2=39.194>10,s3=15.4023>10可以认为该回归方程存在严重的多重共线性

#检验完全多重共线性
import pandas as pd
from statsmodels.stats.outliers_influence import variance_inflation_factor
import numpy as np
# 当VIF<10,说明不存在多重共线性；当10<=VIF<100,存在较强的多重共线性，当VIF>=100,存在严重多重共线性
vif = [variance_inflation_factor(df.values, df.columns.get_loc(i)) for i in df.columns]

探究单个变量与结果之间的可决系数，进行一元线性回归

plt.figure(figsize=(2*6, 5*5))  
for i, col in enumerate(df.columns): 
    train_X = df.loc[:, col].values.reshape(-1, 1)
    # 每一次循环，都取出datafram中的一列数据，是一维Series数据格式，但是线性回归模型要求传入的是一个二维数据，因此利用reshape修改其形状
    train_Y = target
    linearmodel = linear_model.LinearRegression()  
    reg = linearmodel.fit(train_X, train_Y)  
    score = reg.score(train_X, train_Y) 
  
    axes = plt.subplot(5, 2, i + 1)
    plt.scatter(train_X, train_Y)
    # 画出每一个特征训练模型得到的拟合直线 y= kx + b
    k = linearmodel.coef_  # 回归系数
    b = linearmodel.intercept_  # 截距
    x = np.linspace(train_X.min(), train_X.max(), 100)
    y = k * x + b
    # 作图
    plt.plot(x, y, c='red')
    axes.set_title(col + ' Coefficient of determination:' + str(score))
plt.show()

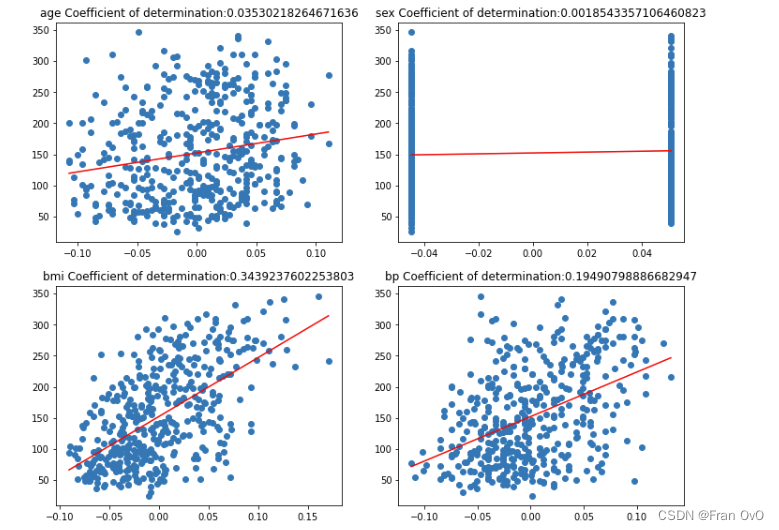
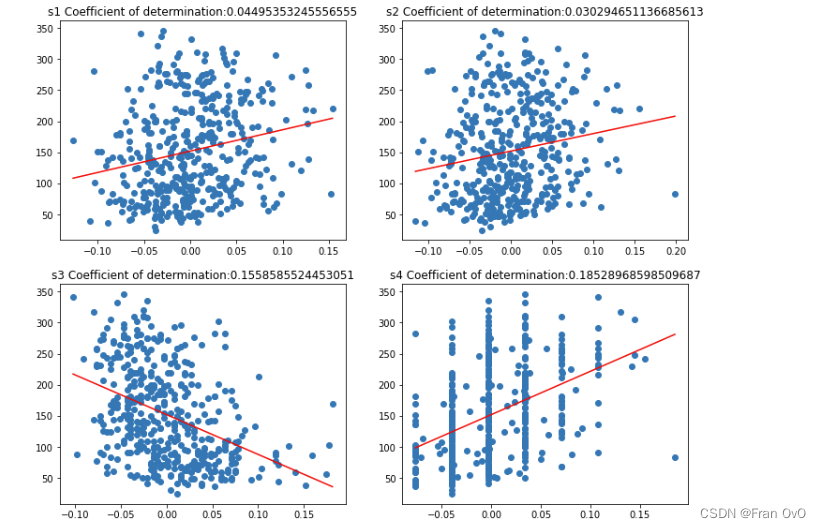
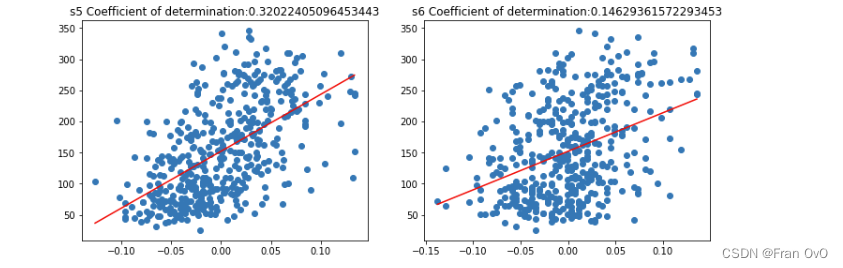
从中可以看出，糖尿病数据集中10的特征，对target的影响大小，从大到小分别是：

[[0.3439237602253803, 'bmi'], [0.32022405096453443, 's5'], [0.19490798886682947, 'bp'], [0.18528968598509687, 's4'], [0.1558585524453051, 's3'], [0.14629361572293453, 's6'], [0.04495353245556555, 's1'], [0.03530218264671636
（这个数据有些指标或多或少有点离谱）

2.5，多元线性回归模型

from sklearn.model_selection import train_test_split
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

train_X, test_X, train_Y, test_Y = train_test_split(data, target, train_size=0.8)

model = linear_model.LinearRegression(copy_X=True, fit_intercept=True, normalize=False)#计算截距
# 3、训练数据
model.fit(train_X, train_Y)
# 4、评估模型
y_pred = model.predict(test_X)
# The coefficients
print("Coefficients: \n", model.coef_)
# The mean squared error
print("MSE:",mean_squared_error(test_Y, y_pred))
# The coefficient of determination: 1 is perfect prediction
print("R2:",r2_score(test_Y, y_pred))

R2的numpy计算方法：

from sklearn.metrics import r2_score
import numpy as np
def test(a,b):
    # a：numpy一维数组，形状是(n,)，表示标签。
    # b：numpy一维数组，形状是(n,)，表示预测结果。
    # print(r2_score(a,b))
    return R2(b,a)
def SST(y_tar):
    y_mean = np.mean(y_tar)
    sst = np.sum((y_tar-y_mean)**2)
    return sst
def SSE(y_hat, y_tar):
    sse = np.sum((y_hat-y_tar)**2)
    return sse
def R2(y_hat, y_tar):#y_hat为预测结果，y_tar为标签目标值
    sst = SST(y_tar)
    sse = SSE(y_hat,y_tar)
    rr = 1-sse/sst
    return rr

多元线性回归求解推导：

MSE： $L=\displaystyle\sum^n_{i=1}\left[ y_i - \left( w_0+w_1x_i\right) \right]^2$

为了 $\left(y- X \beta \right)^T \left(y - X \beta \right)$ 最小

。。。。一堆计算之后（没必要看）

$\beta = \left(X^T X\right)^{-1} \left(X^T y\right)$

#一些numpy操作
# 矩阵拼接
import numpy as np
#拼接
np.concatenate((a,b), axis=1)
# 矩阵乘法
a.dot(b)
# 矩阵转置
a.T
# 矩阵的逆
aa=np.linalg.inv(aa)
#求方差
np.var(a)
#均值
np.mean(a)

计算 $\beta$ :

ones = np.ones([X.shape[0], 1])
X=np.concatenate((X,ones),axis=1)
XT=X.T
XTX=X.T.dot(X)
XTX=XTX.dot(XTX.T)
XTX_1=np.linalg.inv(XTX)
XTY=XT.dot(y)
beta=XTX_1.dot(XTY)

2.6 利用岭回归解决多重共线性问题

from sklearn.linear_model import Ridge

n_alphas = 100
alphas = np.logspace(-5, 0, n_alphas)

coefs = []
for alpha in alphas:
    ridge = linear_model.Ridge(alpha=alpha)
    ridge.fit(train_X, train_Y)
    coefs.append(ridge.coef_)
y_reg_pred = ridge.predict(test_X)
# The coefficients
print("Coefficients: \n", ridge.coef_)
# The mean squared error
print("MSE:",mean_squared_error(test_Y, y_reg_pred))
# The coefficient of determination: 1 is perfect prediction
print("R2:",r2_score(test_Y, y_reg_pred))

ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim())[::-1]
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.show()

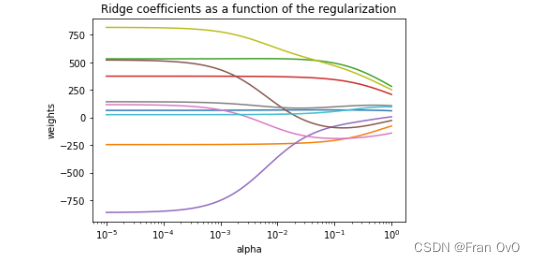
从岭迹图可以看出那些指标对结果显著那些指标不显著

岭回归的数学原理：最小化目标从MSE变成MSE+系数平方和

新的目标是： $\left(y- X \beta \right)^T \left(y - X \beta \right) + \alpha \left(\beta^T \beta \right)$

新的结果是： $\beta = \left( X^T X + \alpha I\right)^{-1}\left(X^T y\right)$

beta = np.linalg.inv(X.T.dot(X) + alpha*I).dot(X.T.dot(y))

2.6，多项式回归

改变特征（变量）的表现形式吧：

eg：一元一次线性回归 $y=w_0+w_1x$ ，变成一元二次线性回归 $y=w_0+w_1x+w_2x^2$

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(d)

d为多项式次数，这是一个改变特征的方法，可以解决多重共线性问题。虽然多项式的加入，对数据的拟合效果有所提高，但是容易出现过拟合或者（龙格现象），这时候给予模型正则化可适当缓解过拟合现象：

例子：进行一元线性回归，拟合sin

（随机数大一点导致过拟合嘿嘿）

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.metrics import mean_squared_error

# 用于训练的数据有20个
train_size = 20
# 用于测试的数据有15个
test_size = 15
# 生成用于训练的 X
train_X = np.random.uniform(low=0, high=1.2, size=train_size)
# 生成用于测试的 X
test_X = np.random.uniform(low=0.1, high=1.3, size=test_size)
# 生成用于训练的 y
train_y = np.sin(train_X * 2 * np.pi) + np.random.normal(0, 0.8, train_size)
# 生成用于测试的 y
test_y = np.sin(test_X * 2 * np.pi) + np.random.normal(0, 0.8, test_size)
plt.scatter(train_X, train_y, c="silver")
plt.scatter(test_X, test_y, c='black')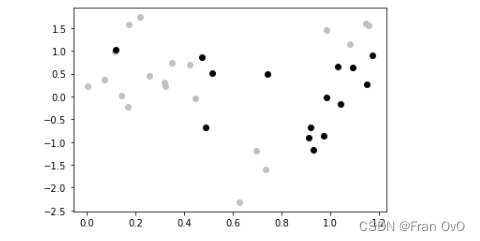

数据转换为多项式

poly = PolynomialFeatures(6) # 次数为6
# 训练数据进行转化
train_poly_X = poly.fit_transform(train_X.reshape(train_size, 1))
# 测试数据进行转换
test_poly_X = poly.transform(test_X.reshape(test_size, 1))

建立线性回归模型

# 1. 建立模型
model = LinearRegression()
# 2. 训练
model.fit(train_poly_X, train_y)
# 3. 预测
train_pred_y = model.predict(train_poly_X)
test_pred_y = model.predict(test_poly_X)
# 4. 评价
print(mean_squared_error(train_pred_y, train_y)) # MSE
print(mean_squared_error(test_pred_y, test_y))   # MSE

说明有些过拟合，那多项式就一个一个变试试：

polys = []   # 每次循环时要保存一个转换器，以便后面调用
models = []  # 每次循环时要保存一个模型，以便后面调用

for n in range(1,7):
    # 0. 数据准备：转换为多项式
    polys.append(PolynomialFeatures(n))  # 次数为n的多项式转换
    train_poly_X = polys[n-1].fit_transform(train_X.reshape(train_size, 1))
    test_poly_X = polys[n-1].transform(test_X.reshape(test_size, 1))
    # 1. 建立模型
    models.append(LinearRegression())
    # 2. 训练
    models[n-1].fit(train_poly_X, train_y)
    # 3. 预测
    train_pred_y = models[n-1].predict(train_poly_X)
    test_pred_y = models[n-1].predict(test_poly_X)
    # 4. 评价
    MSE_train = mean_squared_error(train_pred_y, train_y)
    MSE_test  = mean_squared_error(test_pred_y, test_y)
    print(f"{n}\t{MSE_train:.3f}\t{MSE_test:.3f}")

可以看见多项式为三次时最好

plt.scatter(train_X, train_y, c="silver")
plt.scatter(test_X, test_y, c='black')

n = 3   # 使用6次方模型展示拟合结果

# 准备拟合曲线，先从x入手，得到一系列的x
xR = np.linspace(-0.05, 1.4, 100)

# 将 x 扩展到 n 次多项式
xR_poly = polys[n-1].transform(xR.reshape(100, 1))

# n次方模型保存在models[n-1]处。用它预测得到拟合结果
yR = models[n-1].predict(xR_poly)

print(models[n-1].intercept_)      # n次方模型的参数
print(models[n-1].coef_)           # n次方模型的参数
plt.plot(xR, yR, 'r-')

加入岭回归：

polys2 = []   # 每次循环时要保存一个转换器，以便后面调用
models2 = []  # 每次循环时要保存一个模型，以便后面调用

for n in range(1,7):
    # 0. 数据准备：转换为多项式
    polys2.append(PolynomialFeatures(n))  # 次数为n的多项式转换
    train_poly_X = polys2[n-1].fit_transform(train_X.reshape(train_size, 1))
    test_poly_X = polys2[n-1].transform(test_X.reshape(test_size, 1))
    # 1. 建立模型
    models2.append(Ridge(alpha=0.1))
    # 2. 训练
    models2[n-1].fit(train_poly_X, train_y)
    # 3. 预测
    train_pred_y = models2[n-1].predict(train_poly_X)
    test_pred_y = models2[n-1].predict(test_poly_X)
    # 4. 评价
    MSE_train = mean_squared_error(train_pred_y, train_y)
    MSE_test  = mean_squared_error(test_pred_y, test_y)
    print(f"{n}\t{MSE_train:.3f}\t{MSE_test:.3f}")

画出多项式6次的拟合曲线

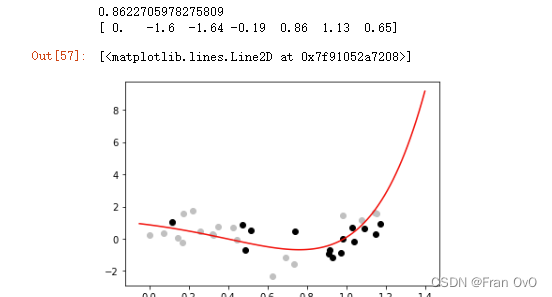
多元线性回归的多项式：

如果一个n元线性回归模型还要进行PolynomialFeatures(d)的变换，最终会得到 $C_{n+d}^d$ (含常数项)

例如，一元线性回归模型经过PolynomialFeatures(6)的变换，会得到7项特征；二元线性回归模型经过PolynomialFeatures(2)的变换，会得到6项特征。

糖尿病数据进行多项式多元线性回归

from sklearn.preprocessing import PolynomialFeatures

polys2 = []   
models2 = []  
for n in range(1,7):
    poly = PolynomialFeatures(n) # 次数为6
    train_poly_X = poly.fit_transform(train_X)
    test_poly_X = poly.transform(test_X)
    models2.append(Ridge(alpha=0.1))
    # 2. 训练
    models2[n-1].fit(train_poly_X, train_Y)
    # 3. 预测
    train_pred_y = models2[n-1].predict(train_poly_X)
    test_pred_y = models2[n-1].predict(test_poly_X)
    # 4. 评价
    MSE_train = mean_squared_error(train_pred_y, train_Y)
    MSE_test  = mean_squared_error(test_pred_y, test_Y)
    R2=r2_score(test_Y, test_pred_y)
    print(f"{n}\t{MSE_train:.3f}\t{MSE_test:.3f}\t{R2:.3f}")

pipeline:将一件需要重复做的事情切割成各个不同的阶段，每一个阶段由独立的单元负责。所有待执行的对象依次进入作业队列。

from sklearn.pipeline import Pipeline
# 1. 建立模型
p = Pipeline([
    ('ppp', PolynomialFeatures(6)),
    ('mm',  Ridge(alpha=0.1)),
])
# 2. 训练
p.fit(train_X, train_Y)
# 3. 预测
train_pred_y = p.predict(train_X)
test_pred_y  = p.predict(test_X)
# 4. 评价
MSE_train = mean_squared_error(train_pred_y, train_Y)
MSE_test  = mean_squared_error(test_pred_y, test_Y)

print(f"{MSE_train:.3f}\t{MSE_test:.3f}")

总结

多重共线性还是用逐步回归好一些,用lasso会比用Ridge好（自己感觉）

Fran OvO

关注

12
点赞
踩
127

收藏

觉得还不错? 一键收藏
1
评论
多元回归分析

回归分析是数据分析中最基础也是最重要的分析工具。通过研究自变量X和因变量Y的相关关系，尝试去解释Y的形成机制，进而达到通过X去预测Y的目的。常见的回归分析有：线性回归，0-1回归，定序回归，计数回归和生存回归。其划分的依据是因变量Y的类型。一、回归的思想回归分析：研究X和Y之间的相关性。相关性：不解释Y:因变量，类型：1）0-1变量：1是好瓜，0是坏瓜。2）定序变量：Y为a,b,c,d或者为1，2，3，4....表示不同的水平3）计数变量：次数，非负整数（完成作业的次数）
复制链接

扫一扫