ANSYS Workbench有限元分析——网格精度确定问题

相信很多初学workbench的同学会碰上一个比较奇怪的问题,就是在同一个模型中如果设置不同的网格精度,计算出来的等效应力(Equivalent Stress)差别会很大,围绕着网格精度的同时也衍生出了以下三个问题,这里我通过一个简单的模型进行仿真求解.

1. 出现最大等效应力的位置是否和网格精度有关?
    
2. 如果网格精度与等效应力呈现正相关是否意味着网格精度越高

应力趋于无穷? / 应力随着网格精度的变化是否会趋于收敛?

1. 直角、圆角或者模型的某些特征是否有影响等效应力?

分析模型:L型支架

材      料:Structure Steel (结构钢)

相关定义:使用solid works生成一个简易的L型支架,并且导入workbench 中,支架的上端面固定(Fixed Support),同时在下断面施加1100N 的弯曲荷载,分别使用5mm、1mm、0.5mm、0.3mm、0.1mm网格求解模型,对比等效应力结果.  

假      设:在弯曲荷载作用下支架的最大应力会出现在内直角处

 

相关的仿真结果如下:
 

 

 

图1

 

图2

 从图1中可以清楚看到,当网格精度设定为5mm时,出现最大应力的位置并不是我们设想的内直角处(这是不符合实际的);但是随着网格精度的提高,最大应力无一例外都出现在预想的内直角处,这也就意味着网格精度不够导致第一次计算结果是不正确的,所以我们的第一个问题就解决了出现最大等效应力的位置是否和网格精度有关?在一定条件下,模型的实际最大等效应力是客观存在的,并且不会随网格精度变化而改变,会出现如上的情况是因为网格精度不够导致的求解不正确.第一个问题解决了,我们要研究的第二个问题来了:如果网格精度与等效应力呈现正相关是否意味着网格精度越高?

从图2来看,随着网格精度的提高,求解的最大应力呈现线性增长,似乎没什么问题,事实上,在给定的条件下,模型的应力必定会趋于某一数值.那到底是什么原因导致的?我们先把这个问题放一放,我再给出另外一组数据.

 

 

图3

 

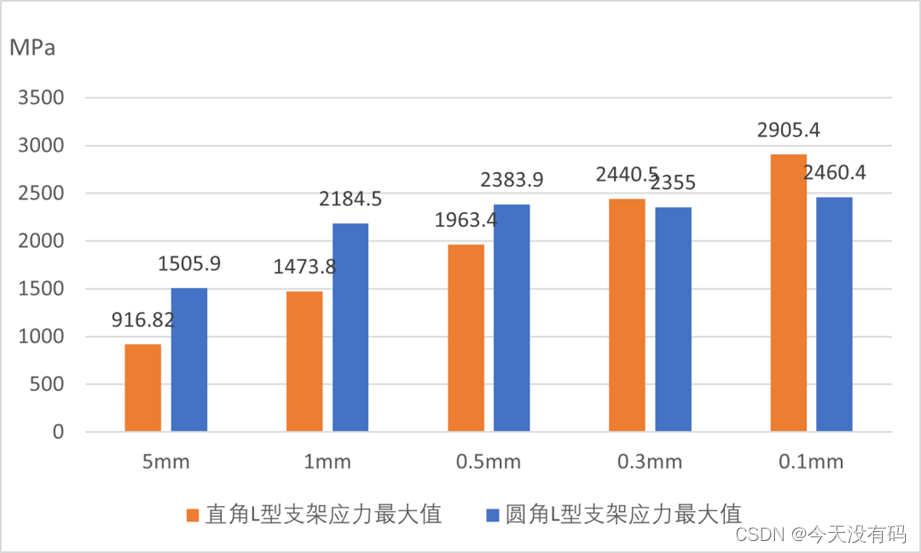
图四

 

第二个模型只是在原模型上将直角处改成了圆角,其余的参数没有变化,得出的结果是在网格精度为0.5mm后的最大等效应力值并没有太大的数值变化,考虑实际中应用几乎可以认为已经趋于收敛了,所以在这里0.5mm的网格精度是足够用的.

在此引入如下两个相关的概念才能更好的回答第二个问题:应力集中和应力奇异性.

应力集中:

应力集中是设计工程师在设计产品过程中不可避免的问题。指受力构件由于外界因素或自身因素几何形状,外形尺寸发生突变而引起局部范围内应力显著增大的现象。多出现于尖角、孔洞、缺口、沟槽以及有刚性约束处及其邻域。

应力奇异性:

受力体由于几何关系，在求解应力函数的时候出现的应力无穷大。根据弹性理论，在尖角处的应力是无穷大(即根据弹性力学的理论难以计算尖角处的应力);由于离散化误差，有限元模型并不会产生无穷大的应力结果，而会形成本例中随着网格的细化,得出的应力值大幅度增加的现象。应力奇异是数学算法问题。应力奇异点般出现在刚性约束和尖角处。我们可以认为应力奇异是应力集中的最极端现象.

所以在第一个直角L型支架模型中,因为应力奇异性的关系其等效应力的求解的结果是不具有参考价值的.但是我们可以通过改结构来避开奇异点,将直角处修改成圆角,值得一提的是当圆角相对于模型非常小,并且趋向直角时候也会出现应力奇异性.
 

那么第二个问题也就解决了,所谓的呈现正相关增长是因为应力奇异性的原因,满足网格精度足够、避开应力奇异那么他的应力也就可以计算出来一个相对稳定的数值.

同时第三个问题:
 

直角、圆角或者模型的某些特征是否有影响等效应力?

自然而然的解决了:因为奇异性的关系,在尖角、孔洞、缺口、沟槽以及有刚性约束处及其邻域导致应力显著增大.

最后真正应该思考的问题是:

(1)应力奇异点在很多模型中都会有，我们怎么办?

答:多数应力奇异点都在结构的非危险部位，可以忽略。

(2)L型支架有应力奇异点，并且在最容易断裂的地方，怎么把它算准?

答:应力奇异点要用数值算法算准是不可能的,但是我们应该对自己提一个问题，我们为什么要算准，从设计角度来说，危险部位应力过度集中已经引起了应力奇异的极端现象，改结构才是工程师应该考虑的问题。

 

图五​

当然了,在分析的直角L型支架模型中并不是说所有的数据都不能使用,变形结果受网格精度影响较小(如图五差别并不大),并且不存在类似应力奇异的问题,因此优先对比位移结果会比较好,位移结果如果出现较大偏差,说明设置存在问题.