最大似然估计法

        参考资料：

        3.1. 线性回归 — 动手学深度学习 2.0.0 documentation (d2l.ai)

        3.4. softmax回归 — 动手学深度学习 2.0.0 documentation (d2l.ai)

        总是听到别人说最大似然、极大似然估计，自己查过，但事后总是忘记到底是什么意思，还是记录一下，加深印象。

1、最大似然

        首先了解一下正太分布，若随机变量 x 具有均值 u 和方差  2（标准差），其正态分布概率密度函数如下：

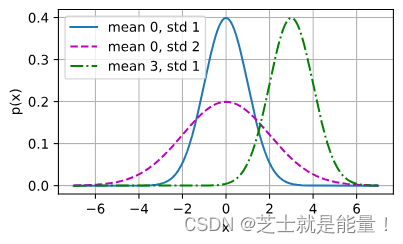
        现在使用该函数作为损失函数计算，计算的函数为y'=ax+b，真实的函数为y。现在可以写出通过给定的x观察到特定y的似然：

        根据最大似然估计法，参数 a 和 b 的最优值是使整个数据集的似然最大的值：

（通俗的说，就是当y'=y时，需要计算的函数与真实的函数最接近，函数有最大值，所以最大似然估计法就是求P(Y=y|x)的最大值。）

 ————————————————————————————分界线————————————————————————————

2、对数似然

        由于历史原因，优化通常是说最小化而不是最大化。 我们可以改为最小化负对数似然−log⁡P(y∣X)。

        由此可以得到最小化负对数似然的数学公式：

3、求损失：

        ①为了让预测的输出总是非负，且概率总和为1，所以我们写为（相当于先写成指数除以指数和的形式，输出从o1变成了概率y1^）：

其中

（ 也写成：，其中 ， ）

       softmax回归对样本i分类的矢量计算表达式为：

        ②在图像分类的例子中，在计算损失时，我们其实并不需要预测概率完全等于标签概率，只要其中一个预测值比其他预测值都大就行了。使用平方损失则过于严格，例如y1^(i)=y2^(i)=0.2要比y1^(i)=y2^(i)=0.4的损失要小很多，虽然两者都有同样正确的分类预测结果。

        所以此处我们使用交叉熵(cross entropy)衡量两个概率分布差异：

        假设训练数据集的样本数为n，交叉熵损失函数(cross entropy loss)定义为(Θ代表模型参数)：

 

（  如果样本只有一个标签，则可写成  ）

        ③再求损失函数（由于y是一个独热编码向量，只需要考虑其为1时的值）：

 

        对损失函数求导：