智慧通信|IEEE Trans. Commun. 论文解读：延迟敏感的能量收集无线传感器的最佳调度、结构特性和近似分析

原文信息

Sharma, Nikhilesh, Nicholas Mastronarde, and Jacob Chakareski. “Delay-sensitive energy-harvesting wireless sensors: Optimal scheduling, structural properties, and approximation analysis.” IEEE Transactions on Communications 68.4 (2019): 2509-2524.

关键字：马尔可夫决策过程、能量收集、延迟敏感无线传感、近似动态规划、结构特性

1 问题背景

能量受限 (energy-constrained) 的无线传感器通常运行在动态信道 (dynamic channel) 和对数据传输延迟非常敏感的环境中。这种传感器具备能量收集能力，能利用环境中的能量（例如环境光或射频能量）维持自身能量所需。这种新兴应用的成功关键在于及时传输采集的数据，而成功部署此类系统的关键是理解此类系统在不同运行条件下的基本性能极限，以及有效计算达到该极限的最佳策略。

文章考虑一个在衰落信道上传输延迟敏感数据的能量收集传感器 (energy-harvesting sensor, EHS)，并将其构建为延迟敏感能量收集调度 (delay-sensitive energy harvesting scheduling, DSEHS) 问题。尽管EHSs可以在不更换电池的情况下自主运行，但能量收集源中的流量负载、能量收集和信道变化随机性对传感器功率管理、传输功率分配和传输调度提出了新的挑战。截止原文发表，许多研究确定了多种计算最优策略的方法，但它们并没有提供对其结构性质的一般性见解。本文作者在文章中将 DSEHS 问题构建为一个马尔可夫决策过程 (Markov Decision Process, MDP)，并分析了其性质，在此基础上量化了在给定能量收集的情况下最小化队列延迟的最优调度策略的长期性能，并提出一种低复杂度的近似值迭代算法来计算近似最优策略，其在近似精度、计算复杂度和内存之间提供了一种可控的权衡。具体而言，文章探讨了以下问题：

1. 如何建模时延敏感的能量收集调度问题 (DSEHS) ？
2. 最优价值函数关于状态是否有良好的结构性质？（最优价值函数即最优策略下使得目标函数能取得的最小值）
3. 如何设计近似值迭代算法？
4. 近似值迭代算法的有效性如何？

2 无线传感器模型

考虑一种在衰落信道上传输延迟敏感数据的时隙单输入单输出能量收集传感器，系统模型如图1所示。该系统包括两个缓冲区：大小为$N_b$的数据包缓冲区和大小为$N_e$的能量缓冲区（电池）。

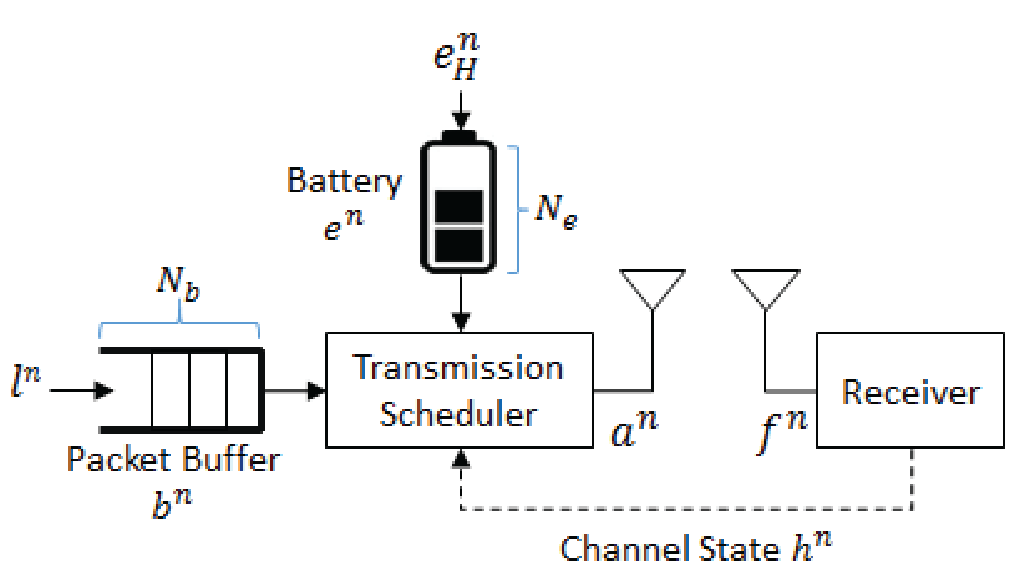
图1：能量收集无线传感器模型

假设时间被划分为长度为$\Delta T(s)$的时隙，系统在第$n$个时隙的状态表示为$s^n=(b^n,e^n,h^n)\in \mathcal{S}$, 其中$b^n$为数据包缓冲状态（即积压的数据包数量），$e^n$为电池状态（即可用能量包数），$h^n$为信道衰落状态。在第$n$个时隙开始时，传输调度器观察系统状态$s^n$，并采取调度动作$a^n$.

信道模型$P^h(h^{\prime }|h)$：假设信道是一个块衰落信道，在每个时隙内信道是恒定的，但在不同时隙之间信道可能发生变化。假设发射机在每个时隙开始时就已知信道状态$h^n$，因此信道状态变化可以建模为具有转移概率函数$P^h(h^{\prime }|h)$的马尔可夫链。

物理层模型$P_{\text{TX}}^n=P_{\text{TX}}(h^n,a^n;BE{P}_{target})$，其中为所有传输设置一个目标比特错误概率(bit error probability, BEP). 假设给定信道状态和目标BEP，发射功率是调度动作$a^n$的非减函数。

能量收集模型：$e^{n+1}=\min (e^n-e_{\text{TX}}^n+e_H^n,N_e)$，其中$e_h^n$表示第$n$个时隙可收集的能量包数量，在第$n$个时隙到达的能量包可以用于未来的时隙，$e_{TX}^n=e_{TX}(h^n,a^n;BE{P}_{target})$表示在时隙$n$消耗的能量包数，并假设传输能量$e_{TX}^n$是能量包的整数倍。

流量模型$b^{n+1}=\min (b^n-f^n+l^n,N_b)$，其中$I^n$表示传感器在第$n$个时隙中产生的数据包数量，$f^n=f(a^n;BE{P}_{target})$为$n$个时隙中成功发送 (goodput) 的数据量。需要注意的是，新到的数据和未成功接收的数据必须在未来的一个时隙中重新发送。

3 延迟敏感能量收集调度问题

DSEHS 问题的目标是在给定可用能量的情况下，确定使平均分组排队延迟最小化的最优策略${\pi }^{\ast }$, 但这并不意味着只要有足够的能量，该策略就会无限地地发送分组——相反，避免在坏信道状态下发送分组，系统倾向于等待在好的信道状态下发送分组，以节省有限的能量收集。另一方面，如果电池 (几乎) 满了，通过传输数据包来消耗能量将为更多收集的能量腾出空间，否则这些能量将因电池大小有限而丢失。

问题表述

现定义一个缓冲区成本来量化大的队列积压。形式上，将缓冲区成本 (buffer cost) 定义为数据队列的积压长度和数据溢出成本之和
c ( [ b , h ] , a ) = b + E f , l [ η max ⁡ { b − f + l − N b , 0 } ] , c([b,h],a)=b+\mathbb{E}_{f,l}[\eta\max\{b-f+l-N_b,0\}], c([b,h],a)=b+Ef,l​[ηmax{b−f+l−Nb​,0}],
值函数$V^{\pi }(s)$
$$V^{\pi }(s)=\mathbb{E}\left[\sum _{n=0}^{\infty }(\gamma {)}^{n}c(s^n,\pi (s^n))|s=s^0\right]$$
表示 EHS 在遵循策略$\pi$时处于某个状态的好（或坏）程度，其中$\gamma$是折扣化因子，且$c(s,a)$和$c([b,h],a)$指代相同的量。因此 DSEHS 问题的目标是确定解决以下优化问题的最优策略${\pi }^{\ast }$:${\min }_{\pi \in \Pi }{V}^{\pi }(s)$ ，其中
V ∗ ( s ) = min ⁡ a ∈ A ( b , e , h ) { c ( [ b , h ] , a ) + γ E l , f , e H , h ′ [ V ∗ ( min ⁡ ( b − f + l , N b ) , min ⁡ ( e − e T X ( h , a ) + e H , N e ) , h ′ ) ] } V^*(s)=\min_{a\in\mathcal{A}(b,e,h)}\{c([b,h],a)+\gamma\mathbb{E}_{l,f,e_H,h^{\prime}}[V^*(\min(b-f+l,N_b),\min(e-e_{\mathrm{TX}}(h,a)+e_H,N_e),h^{\prime})]\} V∗(s)=a∈A(b,e,h)min​{c([b,h],a)+γEl,f,eH​,h′​[V∗(min(b−f+l,Nb​),min(e−eTX​(h,a)+eH​,Ne​),h′)]}

基于动态规划的决策后状态（post-decision states，PDSs）

文章使用决策后状态 [1-3] 而不是传统状态，因为使用PDSs来计算值函数比使用传统状态计算值函数要简单。
决策后状态PDS
$${\tilde{s}}^n=({\tilde{b}}^n,{\tilde{e}}^n,{\tilde{h}}^n)=([b^n-f^n],[e^n-e_{\mathrm{TX}}(h^n,a^n)],h^n)$$
表示在受到可控/已知作用之后，但在受到不可控动态发生之前的系统状态 [1]. 重要的是，下一个状态可以用 PDS 表示如下:
$$s^{n+1}=(b^{n+1},e^{n+1},h^{n+1})=(\min ({\tilde{b}}^n+l^n,N_b),\min ({\tilde{e}}^n+e_H^n,N_e),h^{n+1}).$$
类似传统状态，文章在 PDSs 上定义 PDS 值函数。令${\tilde{V}}^{\ast }(\tilde{s})$表示最优 PDS 值函数，则${\tilde{V}}^{\ast }$和$V^{\ast }$可满足：
$${\tilde{V}}^{\ast }(\tilde{s})=\eta {\mathbb{E}}_l[\max (\tilde{b}+l-N_b,0)]+\gamma {\mathbb{E}}_{l,e_H,h^{\prime }}[V^{\ast }(\min (\tilde{b}+l,N_b),\min (\tilde{e}+e_H,N_e),h^{\prime })],$$
$$V^{\ast }(s)=\underset{a\in \mathcal{A}(s)}{\min }\left\{b+{\mathbb{E}}_f[{\tilde{V}}^{\ast }(b-f,e-e_{TX}(h,a),h)]\right\}.$$
如果数据包到达、能量收集和信道动态是已知且固定的，则可以离线进行 PDS 值迭代。如果动态是非平稳的，那么该算法可以周期在线执行，以随着动态的变化更新PDS值函数。但是如果缓冲区和电池容量足够大，那么任何需要计算和存储每个单一状态的值函数的表格方法由于维度指数增大变得难以处理。此外，如果缓冲区和电池大小是无限的，这种表格式方法就不适用。

离线 (offline) 是指已知数据包到达、能量收集和信道动态下，可以直接计算最优的价值函数，并获得最优策略，从而可以部署执行。在线(online) 是指上述过程未知，在实际部署中需要不断更新和估计，从而不断接近最优策略。

决策后状态价值函数性质

虽然 PDS 值迭代过于复杂，无法在EHS上实现，但利用其迭代结构，利用数学归纳法推导出最优PDS值函数${\tilde{V}}^{\ast }(\tilde{s})$的结构性质。

若一个函数$f(x,y)$在$(x,y)$上有增差 (decreasing differences), 如
$$f(x^{+},y^{+})-f(x^{+},y^{-})\le f(x^{-},y^{+})-f(x^{-},y^{-}),\forall x^{+}\ge x^{-},y^{+}\ge y^{-}$$
则定义函数$f(x,y)$为子模函数 (submodular function).

最优PDS值函数${\tilde{V}}^{\ast }(\tilde{s})$的函数性质包括：

1. 单调性：最优 PDS 价值函数关于$\tilde{b},\tilde{e}$分别是非增和非减的。
2. 增差性：在 PDS 数据队列状态$\tilde{b}<N_b-M_l$下（其中$M_l$是一个时隙下最大数据包到达量），最优PDS价值函数关于$\tilde{b},\tilde{e}$是增差的。

性质1和2表明，在 PDS 数据队列状态$\tilde{b}<N_b-M_l$下，随着队列积压的增加，持有一个额外数据包的边际成本也会增加。此外，额外能量包的边际效益随着可用电池能量的增加而降低。

4. 子模性：最优 PDS 价值函数关于$(\tilde{b},\tilde{e})$是子模的。

性质3表明，数据包和能量数据包是互补的 (complementary); 也就是说，拥有更多的能量包降低了持有额外数据包的边际成本，即当可用能量更多时，额外一个数据包产生的边际成本更小。而持有更多的数据包会增加拥有额外能量数据包的边际效益；换句话说，缓冲区越满，额外能量包的边际效益就越大。

4 近似算法

上述最优策略可以通过如PDS价值迭代或策略迭代算法获得最优策略。尽管如此，由于维度影响，尤其是状态变量需要遍历电池队列、数据队列、信道三个维度，因此文章利用上一节提出最优策略的性质，文章设计了一个 AVI 近似算法，从而降低算法复杂度。

分段平面近似误差有界

为了在缓冲-电池平面上进行空间自适应近似，文章使用四叉树数据结构，其叶节点顶点定义网格，且四叉树的每个叶子被分成两个三角形。所有叶节点的平面共同组成了图2所示的分段平面近似如下。

四叉树构造：设$\mathcal{T}$表示定义在缓冲电池状态对集合上的四叉树，边界框定义如下
$$\text{BB}(\mathcal{T})=\{(b_{-},e_{-}),(b_{+},e_{-}),(b_{-},e_{+}),(b_{+},e_{+})\},$$
其中$0\le b_{-}<b_{+}\le N_b,0\le e_{-}<e_{+}\le N_e$.如果子树是叶节点，那么它可以进一步细分为四个子树。

设$\mathcal{T}(\tilde{h})$表示用于近似信道状态$\tilde{h}$中的PDS值函数的四叉树，现构造 PDS 值函数$\tilde{V}$的近似$\hat{V}$，其中

近似函数首先使用从根开始的递归搜索将$(\tilde{b},\tilde{e})$与包含它的叶节点关联起来。随后，它将$(\tilde{b},\tilde{e})$与包含它的三角形关联起来。这个三角形构成了分段平面逼近平面。最后对近似平面的方程进行求解，可得到近似值$\hat{V}(\tilde{b},\tilde{e},\tilde{h})$.

另一方面，在边界框之外的 PDS对不属于任何叶节点，必须与其最近的叶节点相关联。将它们关联到叶节点的三角形，并将其值近似于该近似三角形定义的平面，类似于边界框内的PDS对。

引入一个算子${\mathcal{A}}_{\mathcal{T}}$作用于PDS值函数$\tilde{V}$，以使用四叉树$\mathcal{T}$给出一个分段平面近似$\hat{V}$, 进而$\hat{V}={\mathcal{A}}_{\mathcal{T}}\tilde{V}$表示其分段平面逼近。设$(\tilde{b},\tilde{e})$位于三角形内，顶点${\mathbf{x}}_i=(b_i,e_i,\tilde{V}(b_i,e_i,\tilde{h}))$，对于$i=1,2,3$的四叉树$\mathcal{T}$, ${\mathcal{A}}_{\mathcal{T}}\tilde{V}-\tilde{V}$的误差有界如下:
$$({\mathcal{A}}_{\mathcal{T}}\tilde{V})(\tilde{b},\tilde{e},\tilde{h})-\tilde{V}(\tilde{b},\tilde{e},\tilde{h})\le \delta ,$$
其中
δ = max ⁡ i ∈ { 1 , 2 , 3 } V ~ ( b i , e i , h ~ ) − min ⁡ i ∈ { 1 , 2 , 3 } V ~ ( b i , e i , h ~ ) δ = \max_{i∈\{1,2,3\}}\tilde V(b_i, e_i, \tilde h)−\min_{i∈\{1,2,3\}}\tilde V(b_i, e_i, \tilde h) δ=i∈{1,2,3}max​V~(bi​,ei​,h~)−i∈{1,2,3}min​V~(bi​,ei​,h~)
依赖于PDS状态$\tilde{s}$，且对于位于同一近似三角形内的所有 PDS 均相等。

近似 PDS 值迭代 (AVI) 算法

算法2给出了AVI (approximate value iteration)算法。

令${\mathcal{T}}^m(\tilde{h})$表示 AVI 算法迭代$m$期间用于近似信道状态$\tilde{h}$中的PDS值函数的四叉树。在AVI算法 (m = 0) 开始时，利用$BB({\mathcal{T}}^0(\tilde{h}))$初始化${\mathcal{T}}^0(\tilde{h})$或使用任意四叉树。因此，${\mathcal{T}}^0(\tilde{h})$作为初始网格点集，使用提出的分段平面逼近方法估计所有$(\tilde{b},\tilde{e})$的值。AVI 算法与 PDS 值迭代有两个关键的区别。

首先，它不是作用于完整的值函数$V_m(b,e,h)$和${\tilde{V}}_m(b,e,h)$，而是作用于相应的近似值函数$J_m(b,e,h)$和${\hat{V}}_m(b,e,h)$.

其次，我们可以在每次迭代后(可选)改进四叉树以满足目标容错。这可以通过细化四叉树${\mathcal{T}}^m$的每个叶节点到$\delta \le {\delta }_{target}$的最粗层次。

作者证明的命题表明AVI算法收敛于$\epsilon -\text{optimal}$ PDS值函数而不是最优的PDS值函数。

计算和内存复杂性分析

文章比较了传统值迭代 [4]、可分解值迭代、PDS值迭代和近似PDS值迭代的计算和内存复杂度。

表格中$|\mathcal{S}|$和$|\mathcal{A}|$分别表示状态和动作的数量，

$|{\mathcal{S}}_b|$、$|{\mathcal{S}}_e|$、$|{\mathcal{S}}_h|$分别表示数据缓冲状态数、电池状态数、通道状态数，

$|\mathcal{L}|$和$|\mathcal{E}|$分别表示数据包和能量包到达分布$P^L$和$P^{eH}$的尺寸大小 (a support of size),

吞吐量分布$P^f$的尺寸大小为$|\mathcal{A}|$,其中$|\Sigma |=|\mathcal{A}{|}^2+|\mathcal{L}|+|\mathcal{E}|+|{\mathcal{S}}_h{|}^2$、${\Pi }_1=\mathcal{L}\times \mathcal{A}\times \mathcal{E}\times {\mathcal{S}}_h$、$|{\Pi }_2|=|\mathcal{L}\times \mathcal{E}\times {\mathcal{S}}_h|$.

本文提出的近似PDS值迭代算法与PDS值迭代算法具有相似的复杂度，但是有两个关键的差异。首先，评估的状态跨越四叉树$\mathcal{T}$而不是$\mathcal{S}$的整个状态空间。其次，在最大四叉树深度$k$处近似与叶子(子树)相关联的状态$(\tilde{b},\tilde{e})\notin \mathcal{T}$的值具有复杂度$O(k)$。因此，更稀疏的近似将在计算和内存效率方面更高。

5 数值结果

最优PDS值函数的结构性质

图4a、图4g和图4b、图4h分别给出了最优PDS值函数和策略。最优PDS值函数(i)在队列积压(命题1和3)中不减小且差异越来越大，(ii)在电池状态(命题2和4)中不增大且差异越来越大。在较好的信道状态下(-4.68 dB)，最优值函数的幅度较小，因为该状态的长期预期成本较低。

图4c和图4d分别为贪心值函数和策略。我们观察到最优策略比贪婪策略更保守，因为它在低电池状态下不传输数据包。这是因为在给定数据到达、能量到达和通道动态的情况下，最优策略权衡其当前调度操作对其未来性能的影响。

图4e、4i、图4f和图4j分别显示了使用动态改进的四叉树生成的近似PDS值函数和策略(在更高的缓冲状态下得到20个更精细的平面)。近似PDS值函数保留了最优PDS值函数的结构。此外，由近似PDS值函数派生的策略(即AVI策略)具有与最优策略相似的结构，并且比最优策略更冒险，但比贪婪策略更谨慎。

近似解与最优调度策略和贪婪策略的性能

贪婪策略在给定可用能量的情况下传输尽可能多的积压数据包，即 a n = min ⁡ { b n , max ⁡ { a : e n ≥ e T X ( h n , a ) } } ) a^n=\min\{b^n,\max\{a:e^n\geq e_{TX}(h^n,a)\}\}) an=min{bn,max{a:en≥eTX​(hn,a)}}).

而文章比较了在考虑伯努利和泊松分布数据包到达的两种情况下AVI、最优和贪婪策略的性能:

• 能量充足:能量包到达分布$P^{e_H}(e_H)=Bern(0.7)$和数据包到达分布$P^l(l)=Bern(x)$.
• 能量不足:与能量充足的情况相比，能量和数据包到达率减少了一半，同时保持相同的能量-数据转率。

在原文图6中，文章展示了在能源充足和不足的情况下，平均排队延迟、电池占用率、缓冲区溢出和电池中断是如何随数据包到达率变化的。每次测量都是通过对相应策略的1250,000个时隙模拟进行平均来进行的。使用所提出的近似PDS值迭代算法计算了标记为AVI-$l$的近似策略(AVI-$l$表示利用提出的有$l$四叉树分支近似PDS值迭代算法计算的近似策略)。

图6a为能量充足情景下的平均排队延迟(左轴)和平均电池占用(右轴)，图6b为相应的平均溢出(左轴)和平均中断(右轴)。文章观察到，随着四叉树经历更多的细分(即，随着$l$的增加)，AVI-$l$的性能在所有四个性能指标方面逐渐提高，并且其性能介于贪婪策略和最优策略之间。这可以归因于这样一个事实，即更粗糙的分段平面近似会导致近似和最优PDS值函数之间的误差更大，但根据这种近似策略比贪婪策略要好。

综上所述，这些结果表明，所提出的解决方案不仅比贪婪策略提供更多的传感器数据（因为当有更少的溢出时，更少的传感器数据丢失），而且在使用更少的能量的同时具有更低的延迟。文章认为同时改进这些指标是问题的内在特征，当优化延迟指标（排队延迟和溢出）时，改进电池指标对于有效地服务传入流量是必要的。

参考文献

[1] N. Mastronarde and M. van der Schaar, “Fast reinforcement learning for energy-efficient wireless communication,” IEEE Trans. Signal Process., vol. 59, no. 12, pp. 6262–6266, 2011.
[2] N. Mastronarde and M. van der Schaar, “Joint physical-layer and system- level power management for delay-sensitive wireless communications,” IEEE Trans. Mobile Comput., vol. 12, no. 4, pp. 694–709, 2013
[3] N. Salodkar, A. Bhorkar, A. Karandikar, and V. Borkar, “An on-line learning algorithm for energy efficient delay constrained scheduling over a fading channel,” IEEE J. Sel. Areas Commun., 2008.
[4] L. Kaelbling, M. Littman, and A. Moore, “Reinforcement learning: A survey,” J. Artif. Intell. Res., pp. 237–285, 1996.