
编者按
针对交通、物流网络中的枢纽选址问题,创新提出了一个机器学习增强组合优化算法的求解框架。在此算法框架的基础上,为单分配 p − p- p−枢纽中位问题(uncapacitated single allocation p − p- p−hub median problem, USApHMP)设计了两个基于图神经网络改进的启发式求解算法。仿真和标准数据集上的大量实验结果表明,所提出的改进算法在求解质量、计算效率的综合表现上优于传统的组合优化方法。这也是机器学习方法在轴辐式网络设计应用中的首次尝试。
1. 背景
在现代物流、交通运输系统中,运输网络结构的设计对于提高效率和降低成本至关重要。其中,轴辐式网络结构(Hub-and-Spoke)是一种常见的设计模式。在轴辐式网络中,以枢纽为轴,负责合并、分发节点之间的流量;以枢纽节点与非枢纽节点之间的运输线路为辐,通过辐线将流量转发至各个非枢纽节点。轴辐式网络通过集中处理流量,优化资源配置,在规模经济效益下产生成本折扣,降低了运输成本。此外,该网络结构减少了出发点-目的地节点(Origin-Destination, O-D)之间的连接,提高了运输系统的稳定性。
枢纽选址问题(Hub Location Problems, HLPs)涉及在轴辐式网络中确定枢纽节点,并确定每个O–D需求的所有运输路线。随着货运和客运需求的激增,枢纽选址问题受到了物流和交通运输领域的广泛关注,特别是在航空客运方面。然而,该问题涉及许多因素,如地理空间信息和O–D对之间的运输需求流量。此外,在大多数情况下,枢纽选址是NP难问题,这使得大规模问题求解变得困难。因此,迫切需要一种高效的方法来应对这一挑战。
在求解枢纽选址问题上,传统的组合优化算法多为精确算法和启发式算法。精确算法(例如Benders分解[1]、拉格朗日松弛[2])通过不断更新上界和下界直到收敛,来获取最优解,但通常计算时间较长,不适用于求解大规模实例。启发式算法包括禁忌搜索算法[3]、模拟退火算法[4]、变邻域搜索算法[5]等,求解速度较快,但容易陷入局部最优解。
随着人工智能技术的快速发展,机器学习在组合优化领域的研究引起了广泛关注。将机器学习应用于组合优化,一方面考虑用机器学习替代计算成本高昂的操作,从而快速获取近似解;另一方面,当专家知识在组合优化问题中不够充分时,机器学习能够通过经验探索来提升现有的决策水平[6]。
2. 算法框架
该算法框架是基于机器学习的两阶段提升算法。其设计的思想为:第一阶段,利用机器学习模型输出节点被选为枢纽的概率/排序分数,从而得到一个潜在的枢纽集合;第二阶段,将枢纽的排序分数、潜在的枢纽集合嵌入到启发式算法中,以提升求解质量和运算效率。算法框架如图1所示。
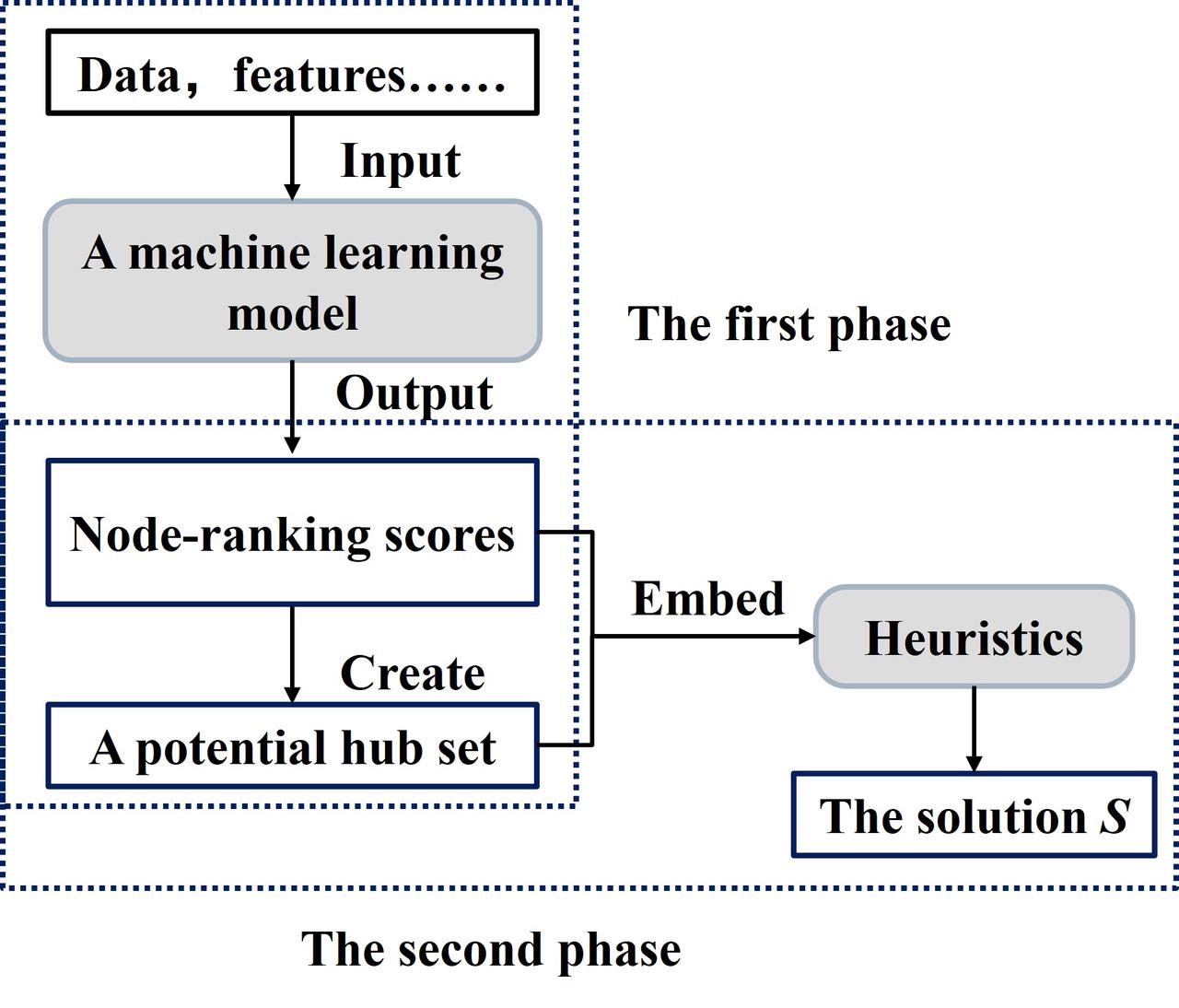
图1:算法框架图
在上述算法框架下,为枢纽选址问题设计具体的算法时,有两个主要问题需要考虑:
(1)如何设计机器学习模型,使其能够输出合理的节点分数?
(2)如何将得到的枢纽排序分数/潜在的枢纽集合嵌入到启发式算法中?
作者以一类经典的枢纽选址问题:单分配 p − p- p−枢纽中位问题(uncapacitated single allocation p − p- p−hub median problem, USApHMP)为具体研究对象,在上述算法框架基础上,提出了两个改进的启发式算法。
3. USApHMP:问题建模
USApHMP问题中,选择的枢纽数量需为 p p p个,每个非枢纽节点只能与一个枢纽节点连通(即,单分配),枢纽节点之间是完全连通的。该问题可建模为如下所示的混合整数规划模型,其中,节点 v ∈ V v \in V v∈V, w v u w_{vu} wvu表示从节点 v v v到节点 u u u的运输需求; c v u c_{vu} cvu表示两个节点之间的距离; O v = ∑ u ∈ V w v u O_v=\sum_{u\in V}w_{vu} Ov=∑u∈Vwvu为节点 v v v产生的总的运输需求(从 v v v运输至其他所有节点),而 D v = ∑ u ∈ V w u v D_v=\sum_{u\in V}w_{uv} Dv=∑u∈Vwuv表示从其他节点到 v v v的运输需求之和。参数 α \alpha α, χ \chi χ 和 δ \delta δ分别为枢纽之间运输、从非枢纽节点到枢纽节点,以及从枢纽节点到非枢纽节点之间运输的成本折扣系数。决策变量 X i j v X_{ij}^v Xijv表示节点 v v v产生的运输需求中,经由枢纽边 i − j i-j i−j运输的需求量, Y v i Y_{vi} Yvi表示节点 v v v是否分配到枢纽节点 i i i。
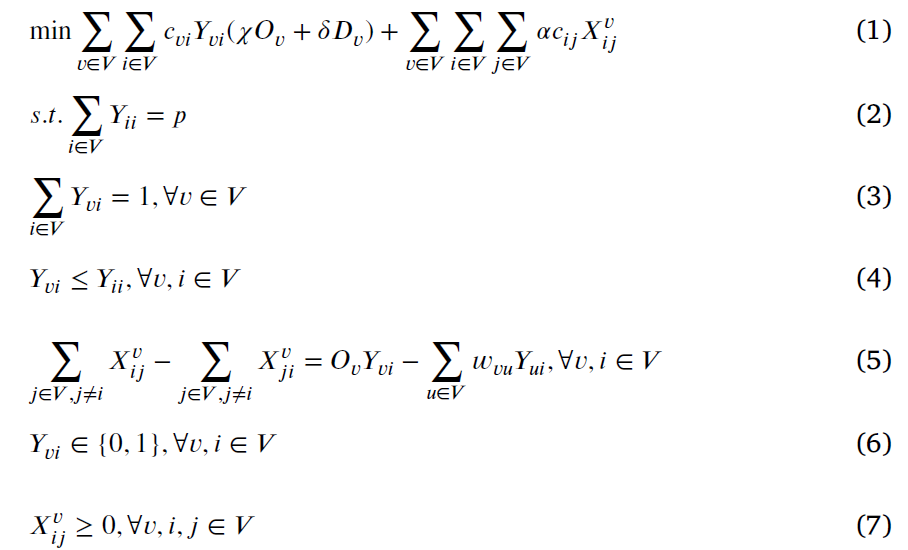
目标函数为最小化总运输成本。约束条件(2)表示选取的枢纽数量为 p p p;约束条件(3)保证了每个节点只能分配给一个枢纽节点;约束条件(4)表示了只有枢纽节点才能被分配;公式(5)是一个流平衡的约束;约束条件(6)和(7)定义了决策变量的取值范围。
4. USApHMP:求解算法设计
在所提出的算法框架下,作者设计了基于深度学习改进的启发式算法以求解USApHMP。算法流程如图2所示。针对轴辐式网络特性,构造了多类型图、多类型特征输入机制,并构建了基于图神经网络的深度学习模型DLHr (a deep-learning based probabilistic hub-ranker),输出节点排序分数。该分数可反映节点被选为枢纽节点的概率,从而生成一个潜在的枢纽集合。将输出结果分别嵌入基于聚类的潜在枢纽集合算法(clustering-based potential hub sets algorithm, CBS)和变邻域搜索算法(general variable neighborhood search , GVNS)中,从而得到两个改进的启发式算法DL-CBS和DL-GVNS。
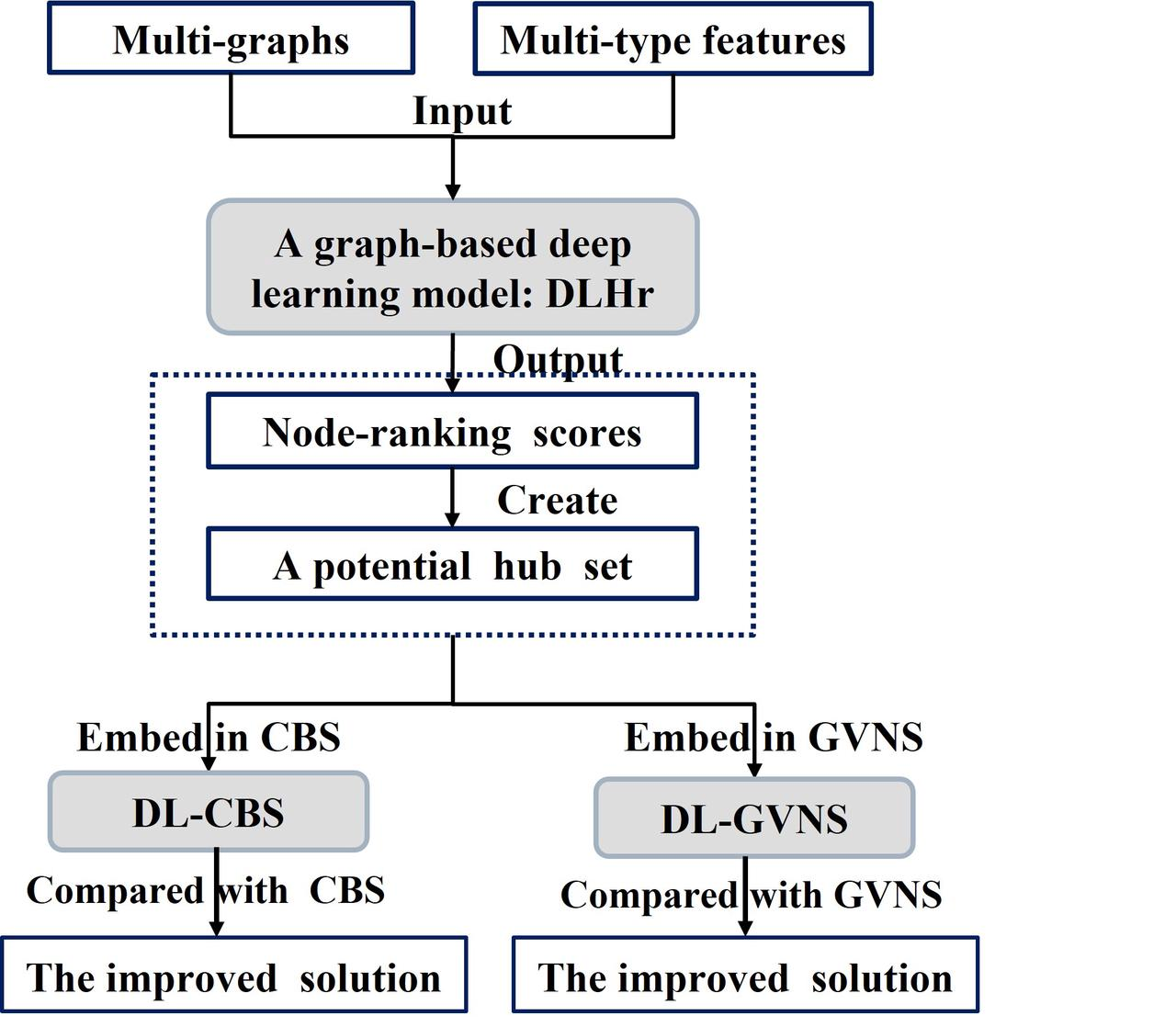
图2:基于深度学习改进的启发式算法流程图
(1)多类型图
为了捕捉运输网络中的重要信息,构建了两种类型的图:即需求-流量图和空间-距离图,分别反映了该运输系统中,节点之间的流量分布关系,和节点的地理空间分布信息。构建方法如下:
需求-流量图:为了捕捉网络中的需求流量信息,构建两个有向加权图,定义为 G O = ( V , E O , A O ) \mathcal{G_O=(V,E_O,A_O)} GO=(V,EO,AO)和 G D = ( V , E D , A D ) \mathcal{G_D=(V,E_D,A_D)} GD=(V,ED,AD),分别用来描述网络中节点的需求生成量( O v O_v Ov)和需求吸引量( D v D_v Dv)。
在图 G O = ( V , E O , A O ) \mathcal{G_O=(V,E_O,A_O)} G








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








