线性旋转变压器最佳变比求解

工科给事中

已于 2022-06-16 11:26:07 修改

阅读量1.6k

点赞数 2

文章标签：自动化

于 2022-06-16 11:12:42 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_53476134/article/details/125310856

版权

复习自动控制元件时，对线性旋转变压器的最佳变比产生了兴趣，查阅了一定的资料，也只是提到“当变压比K=0.52时，在 $\pm 60^\circ$ 的范围内，特性曲线与理想直线的误差最小，一般取K为0.56~0.57”，至于这个结果是怎么推导出来的，没有过多的介绍，这里，我利用一个较为简明的方法推导这个最佳变比。

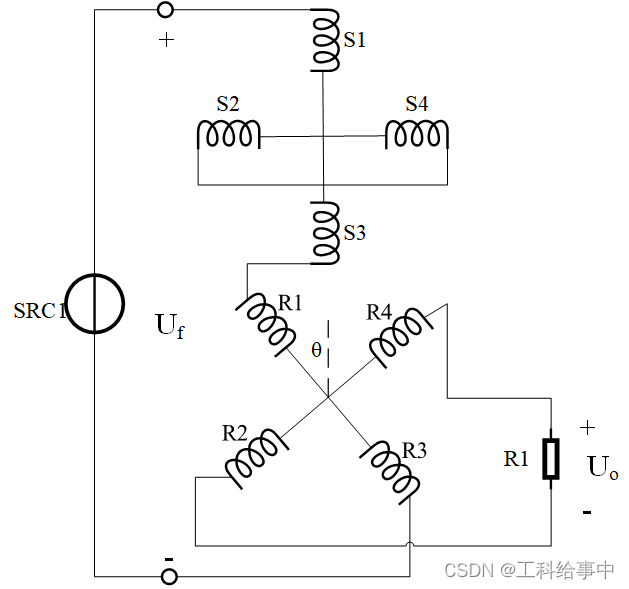
线性旋转变压器接线方法如上图所示，得到的输出电压与输入电压（励磁电压）的关系式为：

$U_o=\frac{K\sin\theta}{1+K\cos\theta}U_f$

由于电源是理想电压源，输入电压 $U_f$ 近似等于电源电动势，可以认为是一个恒定的值，则前面的系数应该是一个与角度值近似满足线性关系的比例式，即：

$\frac{K\sin\theta}{1+K\cos\theta}\approx k\theta,-60^\circ\leq \theta\leq60^\circ$

将上式作适当变形，并利用泰勒公式展开得：

$K\sin\theta\approx k\theta+kK\theta\cos\theta$

$K\theta-K\frac{\theta^3}{6}+K\frac{\theta^5}{120}=k(K+1)\theta-kK\frac{\theta^2}{2}\cdot\theta+kK\frac{\theta^4}{24}\cdot\theta$ （*）

上式对 $-60^\circ\leq\theta\leq60^\circ$ 内的 $\theta$ 均成立，因此应当使高次项正负项对消，同时保留一次项相等，即有：

$K\theta=k(K+1)\theta$ （1）

$-(\frac{kK}{2}-\frac{K}{6})\theta^3+(\frac{kK}{24}-\frac{K}{120})\theta^5=0$ （2）

化简（2）式，得到结果：

$(60-5\theta^2)k-(20-\theta^2)=0\Rightarrow k=\frac{20-\theta^2}{60-5\theta^2}$ （3）

这里的 $\theta$ 应用弧度值单位，则当其最大的时候，即取到 $\pm 60^\circ=\pm\frac{\pi}{3} rad=\pm 1.05 rad$ 的时候，此时：

$k=\frac{20-(\frac{\pi}{3})^2}{60-5(\frac{\pi}{3})^2}=0.347$

而当 $\theta$ 应用弧度值单位，当其最小的时候，即取到0的时候，有：

$k=\frac{20}{60}=0.333$

可见输出比例系数k的变化范围很小，以两个端点值的均值0.34作为输出比例系数，反解变比得：

$K=\frac{k}{1-k}=\frac{0.34}{0.66}=0.515\approx0.52$

这就求得了最佳变比，如果要进一步求更精确的值，可将（*）式多展开几项，求解高次方程，得到的结果与这个形式相差很小，如果要求解最佳变比K的范围，就根据两个端点值，分别代入（3）式中可以得到范围的结果。

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。