Fisher 精确检验与卡方检验(10X单细胞和10X空间转录组的基础知识)

本文链接：https://blog.csdn.net/weixin_53637133/article/details/138146086

本文介绍了Fisher精确检验在比较颜值与数学成绩关联性的例子中如何使用，包括单边检验过程、P值计算以及与卡方检验的比较。同时，给出了Python代码示例，展示了如何在实际数据中运用这两种统计方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Fisher精确检验是基于超几何分布计算的，它分为两种，分别是单边检验（等同于超几何检验）和双边检验。
应用于将对象分成两组后的分类数据，以检查两组分类间是否有显著关系。

举个例子：

我想知道颜值高的人是不是数学成绩也好（数据瞎编的），于是我们随机抽出10个人，5个颜值高，5个颜值低，对应的考试成绩如下表(这个表叫做列联表，英文是contingency table)：

零假设：颜值跟成绩无显著相关性。

为了知道能否拒绝零假设，我们下面做个Fisher精确检验（单边检验）

第一步：想知道零假设是否成立，就要看这组数据是不是随机偶然一抽就能抽到，因此我们计算零假设成立时，即颜值高与颜值低的人，高分低分的数量相同时，得到这样一组数据的超几何概率：

第二步：做完上面这一步还不够。如果行总数与列总数（又叫边际总数）不变，零假设不成立时的极端情况应该是，颜值高的学习都好！那么我们可以得到新的列联表：

这时，可以计算这个表格的超几何概率，

那么Fisher精确检验的P value就是两者加和，即
p值越小，我们越有信心拒绝零假设。如果我们以0.05为显著性水平判断值的话，我们可以认为，颜值高的人，数学学得好。

python 实现

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

obs2 = [[9,3], [1,7]]
aa, bb=stats.fisher_exact(obs2, alternative='greater')
print(aa,bb)

21.0 0.009883305548940234

卡方检验

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，卡方值越大，越不符合；卡方值越小，偏差越小，越趋于符合，若两个值完全相等时，卡方值就为0，表明理论值完全符合。
四格表的卡方计算公式:
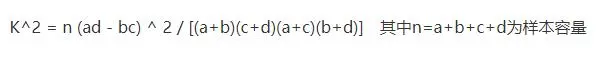
卡方检验一般要求交叉表中的单元格内的数值或者期望值大于5, 当这个条件不满足的情况下, 需要对其进行校正, 一般用Yates’s校正公式计算卡方值. 计算公式是:

Python中我们用scipy模块scipy.stats.chi2_contingency来计算卡方及其P值:

from scipy.stats import chi2_contingency
#未校正的卡方
chi2_contingency([[44, 4], [32, 10]],False)
#下面的结果依次是:卡方值, p值, 自由度, 期望频率
(4.0843179377013969, 0.043282916905174974, 1, array([[ 40.53333333,   7.46666667],
       [ 35.46666667,   6.53333333]]))
#校正过的卡方
chi2_contingency([[44, 4], [32, 10]],True)
(2.9911133861439323, 0.083722586239569685, 1, array([[ 40.53333333,   7.46666667],
       [ 35.46666667,   6.53333333]]))