二项分布的参数p的检验

        设某事件发生的概率为p，做m次的独立检验，以X为发生的次数，则X服从二项分布B(m, p)，则针对X可以做出假设

        定义一个合理的检验,，设置一个阈值C：

                F : 当 X < C时，接受H0，否则拒绝H0

        其中，则设置犯第一类错误的概率为

       因此，现在设置一个显著性水平，使得其犯错误的概率在一定的小范围内：

 那么现在，就转化为使得。从直观上面来说，“p值越小，X取到较小值的概率就越大”，则说明是关于p的减函数,也就是说,是随p的增函数。因此，当p = p0时，可以达到最大:

.

         但是，不一定每次都可以取到一个使方程成立的整数C，较常见的是存在一个使得：

此时，一般选取的是,因为这样是降低了检验水平，增加量拒绝域，降低了第一类错误的概率。因此，最终可以转化为方程，其实就是为了求解：

可以这样理解这一个公式，现在需要找到一个C。跳出这个公式，这个C就是我进行假设检验的阈值，如果超过了这个阈值，我就认为，在显著性水平为的情况下，拒绝原假设。回归公式，要是的右边的公式成立，现在是已知的，则需要在满足条件的下C的最小值。结合二项分布的图像，

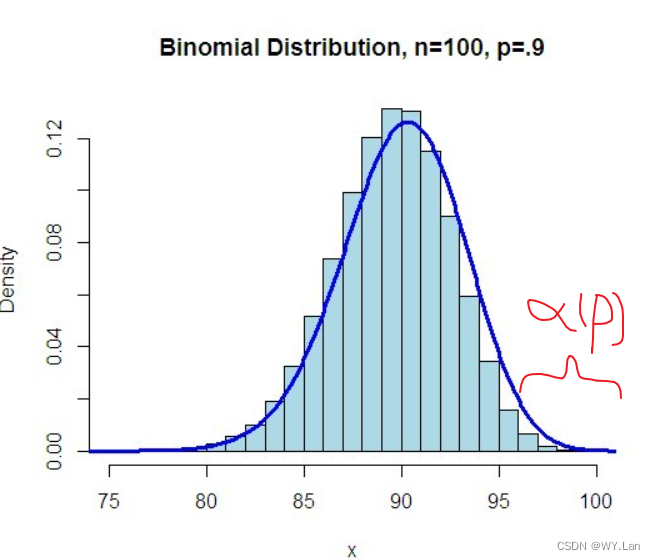
因此，C的取值范围其实就是, C其实可以是慢慢的向右。因此，最终可以求出这个阈值，再对采用中的样本的是否大于,若大于，则拒绝原假设，认为原假设是错误的。

        以上就是二项检验的全部内容，整个过程还是比较清楚的。

        下面开始胡说八道，有点自己的想法，但是不知道怎么表达：主要是针对进行假设检验中最后一步的计算。

        在定义显著性性水平和构造一个检验统计量之后，需要判断所采的样本是否满足阈值的条件。根据限制条件，找到检验统计量的阈值，再计算采集样本中的检验统计量的值，再对检验统计量进行判断。