二项分布（Binomial Distribution）

二项分布的基本描述：

　　　在概率论和统计学里面，带有参数n和p的二项分布表示的是n次独立试验的成功次数的概率分布。在每次独立试验中只有取两个值，表示成功的值的概率为p，那么表示试验不成功的概率为1-p。这样一种判断成功和失败的二值试验又叫做伯努利试验。特殊地，当n=1的时候，我们把二项分布称为伯努利分布。

　　　二项分布频繁地用于对以下描述的一种实验进行建模：从总数量大小为N的两个事物中进行n次放回抽样，以某一事物为基准，计算成功抽取这个事物的次数的概率。要注意的是必须进行的是放回抽样，对于不放回抽样我们一般用超几何分布来对这样的实验进行建模。

二项分布的概率质量函数：

　　　一般来说，如果一个随机变量X满足二项分布的话，那么它一定有一个参数n∈ ℕ且还有一个参数p∈ [0,1]。这样的话，我们可以把关于X的二项分布写成X ~ B(n, p)。对应的概率质量函数如下。

　　　这里k = 0, 1, 2, ......, n，并且原括号是组合的表示形式，组合的计算公式如下。

　　　这个公式表示的从n个数中取k个数构成一个组合能有多少种不同的取法。整个二项分布我们可以描述为求n次独立的伯努利试验，成功k次的概率是多少。由于一次成功的概率是已知的，因此我们必须求出n次试验中，成功k次可能发生在哪次试验中，一共有多少种可能都要求出来，因此求的就是n取k组合数目。

二项分布的均值：

　　　如果存在X~B(n, p)这样一个二项分布，也就是说X是呈现出二项分布的随机变量，n表示试验的总数，p表示每个试验中得到成功结果的概率，那么X的期望值如下。

　　　证明在最下面的维基百科链接中。

二项分布的方差：

　　　同样的，如果存在X~B(n, p)这样一个二项分布，也就是说X是呈现出二项分布的随机变量，n表示试验的总数，p表示每个试验中得到成功结果的概率，那么X的方差如下。

　　　证明在最下面的维基百科的链接中。

二项分布的和：

　　　如果存在两个独立的二项分布X~(n, p)和Y~B(m, p)，要注意的是它们在一次试验中成功的结果具有相同的概率p，那么X+Y也是一个二项分布。这样一个和的分布可以表示为Z=X+Y ~ B(n+m, p)：

　　　但是，如果X和Y一次试验成功的结果没有相同的概率p，那么X+Y的和的方差就会比B(n+m, p的均值)这样一个二项分布的方差要小。

使用二项分布近似其它的分布：

　　　①近似正态分布：当n足够大，且二项分布的近似曲线不是很弯曲的时候，我们可以用以下式子使二项分布B(n, p)近似于正态分布。并且我们可以用适当的连续性校正（continuity correction）来改善这样一个近似的正态分布。

　　　②近似泊松分布：在np固定不变，n趋于无穷大，p趋于0的时候，我们可以用一个二项分布来近似一个泊松分布。这样的话，泊松分布的λ=np。

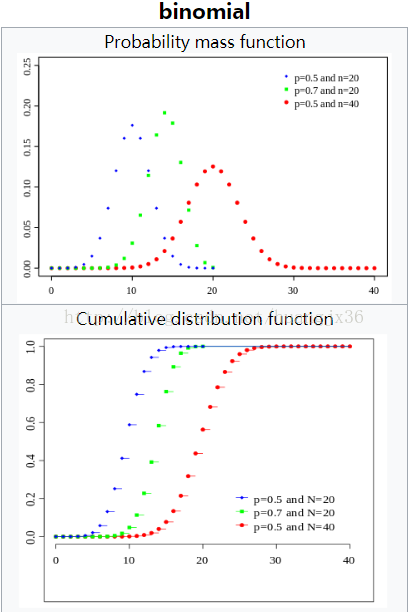
二项分布的属性图：

参考资料：

二项分布-维基百科  https://en.wikipedia.org/wiki/Binomial_distribution