【论文翻译】编码超材料、数字超材料和可编程超材料

论文名称：Coding metamaterials, digital metamaterials and programmable metamaterials
期刊名称：Light: Science & Applications
发表年份：2014年

摘要

  超材料是一种人工结构，在宏观尺度上可以用有效介质参数来描述。这些超材料被称为“模拟超材料”。本文中，我们通过两个步骤提出“数字超材料”。首先，我们提出了“编码超材料”，它仅由两种类型的单元构成，相位响应为0和$\pi$，我们分别将其命名为“0”和“1”编码元素。通过对“0”和“1”单元进行可控序列编码（即1位编码），可以对电磁波进行操纵，从而实现不同的功能。编码超材料的概念可以从1位编码扩展到2位或更高位的编码。在2位编码中，使用四种相位响应分别为$0$、$\pi$、$\pi$和$3\pi /2$的结构单元来模拟“00”、“01”、“10”和“11”四种编码元素。在控制电磁波方面，2位编码比1位编码具有更强的自由性。其次，我们提出了一种独特的超材料单元，它的“0”和“1”相位响应由偏置二极管控制。基于这种单元，我们提出了"数字超材料"，它的单元具有“0”或“1”两种编码状态。使用现场可编程门阵列，实现了对数字超材料的数字化控制。通过编程产生不同的编码序列，单个数字超材料具有以不同方式操纵电磁波的能力，从而实现了“可编程超材料”。上述概念和相关物理现象均通过数值模拟和超表面实验加以证实。
关键词：编码 数字 超材料 超表面 可编程

  超材料是一种人造结构，它被设计用来获得不寻常的特性，例如负折射、完美透镜、超透镜以及隐形斗篷等。目前的超材料根据其结构排列大致分为两类：均质（具有周期结构）和非均质（具有非周期结构）。先前对超材料的研究主要集中在亚波长尺度的周期性结构上，这些结构可以用宏观的均匀介质参数来描述。使用特殊的单元结构设计，可以根据有效介电常数和磁导率的极值（例如负折射率导致的负折射和完美透镜效应和零折射率导致的高定向发射和隧道效应）或有效介质的各向异性来控制电磁波。对于有效介质理论无法描述的周期性结构，例如光子晶体，可以通过允许和禁止能带来操纵电磁波。相反，结构形状呈梯度变化的亚波长非周期结构设计，在控制电磁场方面具有很大自由性，其结构通常为宏观非均匀超材料。变换光学为设计理想的各向异性和非均匀超材料提供了强大的工具，可以实现对电磁波传播、偏振和散射特性的任意控制，以产生不同寻常的物理现象或制造新型器件，包括隐形斗篷，聚光器，视错觉和新型透镜。传统的几何光学方法和费马原理为设计梯度折射率超材料提供了一种可替代发方法，用于制造高性能天线，高分辨率成像透镜和低散射截面，甚至用于执行数学运算。近期，周期性或梯度超表面也被研究用于操纵电磁波。
  基于有效介质理论，现有的超材料，无论是周期结构还是非周期结构，通常都具有连续的宏观介质，具有均匀或不均匀的有效介电常数和磁导率。“连续”特性导致现有的超材料可被归类为“模拟超材料”。Della Giovampaola和Engheta最近提出了一种通过“数字超材料比特”在空间的恰当混叠来构建“超材料字节”的方法，其中“数字超材料比特”是一些具有不同材料特性的人工原子（例如具有正介电常数的Si和具有负介电常数的Ag）。然而，由此产生的超材料字节仍然用有效介质参数来描述。在这里，我们提出了"编码超材料"、“数字超材料"和"可编程超材料"的一般概念。在这里，数字超材料是指单个可通过数字控制的超材料，能够获得明显不同的功能。为了实现编码超材料，我们将引入两种相位响应分别为0和\pi的单元格，来模拟1位数字信号的“0”和“1”编码，以便可以使用现有的数字技术进行控制。这些“0”和“1”码元不需要用宏观介质参数来描述。通过在编码超材料中设计“0”和“1”的编码序列，我们可以操纵电磁波来获得不同的功能。这个概念也可以扩展到2位或更高位实现。
  事实上，反相法已经在天线和光学领域得到了广泛的应用。通过设计一种薄的人造完美磁导体（相位为0），并将完美磁导体单元与完美电导体（相位为$\pi$）单元在一个棋盘状结构中结合，在平面电磁波正常入射下，任何反射将被抵消，雷达横截面（RCS）也随之减少。同样，在衍射光学中，双相（或多相）光栅也得到了深入的研究，它是由根据设计好的蚀刻模式的制作的多层介电掩模构成的。例如，对于相移$\pi$，蚀刻深度必须近似等于光的波长，对于微波来说，该波长是十分大的。相关领域还包括空间光调制器，它对波束施加某些形式的空间变化调制。通过与超材料单元的结合，可以在太赫兹频段实现超材料吸收空间光调制器的。
  在本文中，我们提出了编码超材料，并通过使用不同的“0”和“1”超材料单元编码序列证明了其对电磁波的调控能力。我们进一步提出了一种独特的超材料单元，它可以实现由偏置二极管控制下的“0”和“1”编码切换。然后，我们构建了一个数字超材料，它由只具有“0”或“1”状态的单元组成。采用现场可编程门阵列（FPGA）硬件，实现了对数字超材料的数字化控制。通过数值模拟和实验，我们证明了单个数字超材料在FPGA程序控制下具有独特的操纵电磁波的能力，从而实现了"可编程超材料”。

材料与方法

1位编码超材料

  本文中的所有结果都基于编码超材料的概念。我们从1位编码的超材料开始。如图1(a)所示，我们考虑一个特殊的超表面，它由二进制数字元素"0"或"1"组成。数字单元的物理实现并不是唯一的，但它需要不同的响应来获得显著的相位变化，以便有较大的自由性来控制电磁波。在二元情况下，相位差的最大值为$\pi$（或180°）。因此，我们将编码“0”设计为相位响应为0的超材料单元，将编码“1”设计为相位响应为$\pi$的超材料单元。这样，相位响应为“0”和“1”的单元可以简单定义为${\phi }_n=n\pi ,(n=0,1)$。可以选择完美的磁导体和电导体作为最简单的“0”和“1”元素。但是，为了达到更宽的带宽，我们利用印在电介质衬底上的亚波长方形金属片来实现二进制码元（参见图1(b)中的插图）。衬底的厚度为h=1.964 mm，介电常数为2.65，损耗角正切为0.001；所述金属贴片厚度为t=0.018 mm，宽度为w；单元的排列周期为a=55 mm。当贴片宽度分别设计为4.8 mm和3.75 mm时，在宽频带的相位差约为180°。特别是在8.1GHz到12.7GHz范围内，相位差在135°到200°之间（在8.7GHz和11.5GHz时恰好是180°）。因此，我们使用w=4.8 mm的贴片作为“0”编码单元，W=3.75 mm的贴片作为“1”编码单元，它们很容易在单层介电板上制造以构建超表面。注意，“0”编码单元的绝对相位响应在特定频率下可能不为0，但这种情况不会影响任何物理特性，因为相位可以归一化为0。

图1：1位数字超表面和编码超表面。(a) 1位数字超表面仅包含两种类型的单元：“0”和“1”。(b) 方形金属贴片单元结构（插图），以实现“0”和“1”单元以及一系列频率点对应的相位响应。(c, d) 两个1位周期编码超表面，通过设计“0”和“1”元素的编码序列来控制波束的散射：（c）010101…/010101…编码和 (d) 010101…/101010…编码。

  与现有模拟超材料利用有效的介质参数或特殊的色散关系来控制电磁场相比，编码超材料只是通过“0”和“1”码元组成的不同编码序列来操纵电磁波。例如，在周期编码序列为010101…/010101…时，正常入射的波束主要被超表面反射到两个对称定向的方向，而在周期编码序列为010101…/101010…/010101…/101010…时，正常入射的波束将主要被反射到四个对称定向的方向，如图1©和1(d)所示。为了定量地说明上述物理现象，我们考虑一块普通的正方形超表面，它包含$N\times N$个维度为D的等大方格，其中每个方格对应一个由“0”和“1”编码单元组成的子数组，如补充图S1所示。“0”和“1”方格的分布可以是任意的。假设每个方格的散射相位为$\phi (m,n)$，相位响应为0°或者180°。当平面波垂直入射时，超表面散射波的远场方向图函数可以表示为
$$f\left(\theta ,\phi \right)=f_e\left(\theta ,\phi \right)\cdot \sum _{m=1}^M\sum _{n=1}^N{e}^{-j\phi \left(m,n\right)+kDsin\theta \left[\left(m-\frac{1}{2}\right)cos\phi +\left(n-\frac{1}{2}\right)sin\phi \right]}$$   其中$\theta$和$\phi$分别为任意方向的俯仰角和方位角，$f_e(\theta ,\phi )$为每个单元的反射模式函数。注意，“0”元素的绝对相位响应可以放在$f_e(\theta ,\phi )$中，以确保其相对相位差为0。因此，超表面的方向性函数$Dir(\theta ,\phi )$可表示为
$$Dir\left(\theta ,\phi \right)=\frac{4\pi {|f\left(\theta ,\phi \right)|}^2}{{\int }_0^{2\pi }{\int }_0^{\pi /2}{|f\left(\theta ,\phi \right)|}^{2}sin\theta d\theta d\phi }$$   这里$f_e\left(\theta ,\phi \right)$项被消去了。从上述方程中，我们清楚地看到通过编码超表面单元格对散射场实现的控制。

图2 ：1位周期编码超表面的全波仿真结果，以证明它们在电磁波正常入射下通过不同编码序列控制散射模式的能力。(a-c)具有周期编码序列的1位超表面结构：(a) 00000…/00000…， (b) 010101…/010101…，(c) 010101…/101010…以及它们在垂直于超表面的观测平面上相应的近场分布。(d-f)超表面的编码序列为以下几种情况时，方程(1)的计算结果分析：(d) 00000.../00000...、(e) 010101.../010101...和(f) 010101..../101010...，通过使用不同的编码序列生成单个主要散射波束、两个主要波束和四个主要波束。(g-i) 编码超表面的全波仿真结果，编码序列为 (g) 00000.../00000...、(h) 010101.../010101...和(i) 010101.../101010...，这与分析预测非常吻合。

表1：不同N值下的最优化编码（RCS：雷达反射截面积）

图3：非周期1位编码超表面抑制电磁波正常入射下的散射主瓣的全波仿真和测量结果。(a) 具有表1中优化后的1位编码序列的超表面结构。(b) 优化后的1位编码超表面的F4B 电介质衬底制作样品。(c)在7.5至13 GHz频率范围内单基地RCS降低的模拟结果和测量结果。(d-f) 在(d) 8 GHz、(e) 10 GHz和(f) 11.5 GHz频率下双基地RCS散射模式的3D仿真结果。据观察，编码超表面将入射的电磁能量重新分散到所有方向，每个方向的电磁能量非常小，从而可以显著减少单基地和双基地的RCS。

  例如，当所有单元都设置为“0”编码时，我们很容易推导出 $$\left|f_1\left(\theta ,\phi \right)\right|=C_1|cos{\psi }_1+cos{\psi }_2|$$ 当编码序列的选择如图1©或(d)所示时，有
$$\left|f_2\left(\theta ,\phi \right)\right|=C_2|sin{\psi }_1+sin{\psi }_2$$ 或者
$$\left|f_3\left(\theta ,\phi \right)\right|=C_3|cos{\psi }_1-cos{\psi }_2$$ 其中C1、C2和C3为常数，${\psi }_1=\frac{1}{2}kD(sin\theta cos\phi +sin\theta sin\phi )$，${\psi }_2=\frac{1}{2}kD(-sin\theta cos\phi +sin\theta sin\phi )$。补充信息中对上述表达式的分析表明，在不同的编码模式下，正常入射波被分散为单个主要波束、两个主要波束和四个主要波束，图2中的全波模拟证实了这一点。注意，分析预测（图2d-2f）在所有情况下都与全波模拟（图2g-2i）很好地保持一致。因此，我们可以利用式（1）和式（2）设计复杂的编码序列，实现编码超表面更高级的功能。
  在实际应用中，我们期望能够通过适当编码“0”和“1”单元来减少金属表面的RCSs。事实上，隐形斗篷运用了通过迫使电磁波在目标周围弯曲来减少RCSs的方法，而完美的吸收器则运用了通过吸收所有入射电磁波来减少RCSs的另一种方法。在这里，我们提出了一种通过使用特殊的“0”和“1”编码将电磁波的能量重新分散到各个方向，从而降低单基底和双基地RCSs的新机制。对于相同尺寸的金属板，编码超表面引起的RCS减小为
$$RCSreduction=\frac{{\lambda }^2}{4\pi N^2{D}^2}\underset{\theta ,\phi }{\mathrm{Max}}[Dir\left(\theta ,\phi \right)]$$   其中$\lambda$是自由空间中的波长。通过优化“0”和“1”单元格的编码序列，可以达到最佳的RCS降低效果，当D固定为$\lambda$时，不同方格数量（N）的优化后编码如表1所示，其中水平方向和垂直方向的编码序列相同。实际上，优化后的代码可以在宽带上运行。尽管这种编码受制于条件$D=\lambda$，但当$D/\lambda$从0.6变化到3.0时，RCS减少几乎保持不变，如图补充图S2(a)所示。请注意，N越大，RCS降低效果越好。当N=20时，在较宽的频带内对RCS的降低可达-23dB。为了进一步保证宽带性能，我们证明了当“0”和“1”单元之间的相位差在180°附近时，优化后的编码序列近似有效（如补充图S2(b)所示）。对于所有情况，当相位差在145°到215°之间变化时，可以保证RCS至少降低-10dB。

图4：2位编码超表面单元及其相位响应。(a) 由不同大小的方形金属贴片构成的“00”、“00”、“00”和“00”单元（从左到右）。(b) “00”、“00”、“00”和“00”单元的相位响应。

图5：2位编码超表面在不同编码序列下对电磁波波的控制。(a)编码序列为 0001101100011011时的周期性2位编码超表面。以及垂直于超表面的观察平面上的近场分布。(b) 周期2位编码超表面的三维远场散射模式。我们观察到随着“00”、“01”、“10”和“11”编码产生的梯度相位变化，正常的平面入射波被反射到一个倾斜的角度，这与广义Snell定律一致。(c) 使用优化后的2位编码序列构建的非周期性超表面。(d) 在7-16GHz的频率范围内，单基地RCS缩减的仿真结果。(e-h) 在8GHz(e)、10GHz(f)、13GHz(g)和15 GHz(h)下的三维双基地RCS模式的仿真结果。相比1位编码超表面，2位编码超表面可以在更宽的频带上提供显著的RCS缩减。

  为了验证上述物理现象，我们基于优化后的编码序列设计并制作了一个包含8×8个单元的超表面，如图3(a)和3(b)所示。超表面的边缘长度为280 mm，每个方格的宽度为35 mm，每个大的方格由7×7个“0”或“1”单元组成。图3(a)和3(b)中的图案是根据N=8时的优化编码序列00110101在水平和垂直方向上对称设计的。在制作过程中，使用了商用介质板（F4B），其参数与仿真中的完全相同。使用商业软件CST Microwave Studio仿真得到了正常入射波（虚线）下宽频带范围内的单基地RCS降低的结果如图3©所示。注意，反方向RCS的-10dB带宽范围为7.8-12 GHz，这与相位差一致。从测量系统中获得的实验结果（图3©中的实线）如图补充图S3所示，可证明在宽频带中单基地RCSs得到显著降低。为了观察双基地的散射特征，图3(d)-(f)给出了超表面在8GHz、10GHz和11.5 GHz三个代表性频率下的三维散射图。如图所示，散射场在各个方向上都被抑制在低电平，归一化双基地RCSs始终小于-10 dB。这是因为编码超表面被设计为将入射的电磁能量反射到各个方向，根据能量守恒原理，向每个方向反射的电磁能量都很小。在10GHz时，入射波方向的最小峰值（低于-10 dB）是由相对较大的相位差（约为203°）引起的（图1(b)）。

图6：用于实现数字超表面及其相位响应的超材料单元。(a) 当偏置二极管分别为“OFF”和“ON”时，超材料单元的结构表现为“0”和“1”编码。(b) 在不同频率下，当偏置二极管的状态分别为“OFF”和“ON”时，超材料单元的相位相应。

2位编码超材料

  编码超材料的概念可以从1位编码扩展到2位或更高位编码。在2位编码中，需要使用具有四种不同相位响应的单元格来模拟“00”、“01”、“10”和“11”编码。相比1位编码，2位编码在操控电磁波时具有更大的自由性，但需要更复杂的数字控制技术。与1位的情况类似，2位编码超材料中的四种单元格应具有$0$、$\pi /2$、$\pi$和$3\pi /2$的相位响应，分别对应于“00”、“01”、“10”和“11”编码。因此，相位相应${\phi }_n$可以简单定义为${\phi }_n=n\pi /2,(n=0,1,2,3)$。
  为了实现这些超材料单元，我们仍然利用在电介质衬底上印制不同尺寸的方形金属贴片的方法来设计宽带的“00”、“01”、“10”和“11”，如图4所示。使用2位编码的超材料或超表面，我们能够更灵活地设计编码单元，以获得更广泛的应用。例如，我们设计了一个简单的周期编码序列0001101100011011…，如图5(a)所示。由于相邻的“00”、“01”、“10”和“11”四个单元具有梯度相位变化，根据广义斯涅耳定律，正常入射波将被反射到一个倾斜的角度，其近场仿真结果和图5(a)和5(b)所示的三维远场散射方向图证实了这一点。在实际应用中，我们在与1位编码相同尺寸的超表面上优化了2位编码序列，以减少金属表面的RCSs，优化后的2位编码如图5©所示。单基地RCSs的仿真结果表明，2位编码超表面具有更好的性能（图5(d)），在更宽的7.5-15 GHz频段内RCS降低了-10 dB。图5(e)-5(h)所示的8GHz、10 GHz、13 GHz和15 GHz频点的三维散射图进一步证实了2位编码超表面抑制双基地RCSs的强大能力。

结果与讨论

  基于编码超材料的概念，我们不仅能够通过改变“0”和“1”（或“00”、“01”、“10”和“11”）数字编码的编码序列来控制电磁波，而且还能够创建实际的数字超材料和可编程超材料。

图7：(a-d) 频率为8.3GHz时，在不同编码序列：(a) 00000，(b) 11111，(c) 01010和(d) 00101下一维数字超表面散射模式的数值仿真结果。 (e-f) 频率为8.6GHz时，在不同编码序列：(e) 00000，(f) 11111，(g) 010101和(h) 001011下一维数字超表面散射模式的实验结果。(i) 实现FPGA硬件控制下的可编程超表面的流程图。

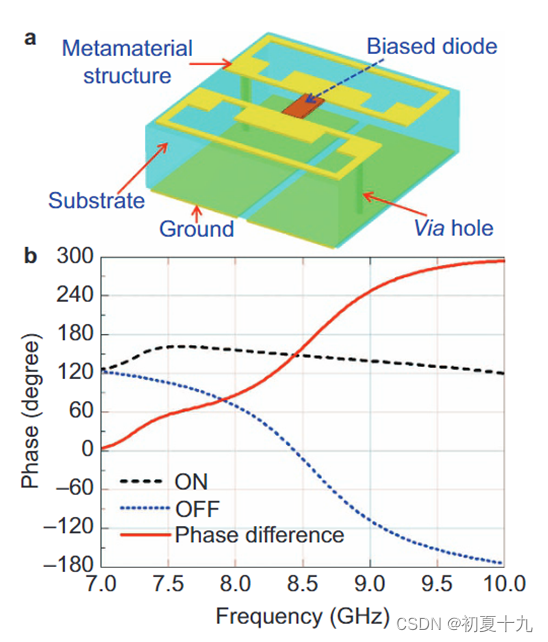
数字超材料

  在上一节中，我们使用两种单元来实现1位编码超表面中的“0”和“1”编码。为了数字化控制“0”和“1”的响应，我们提出了一种独特的超材料单元结构，如图6(a)所示。在介电常数为2.65、损耗角正切为0.001的F4B衬底上表面印制了两个平面对称金属结构（补充图S4），两个结构通过偏置二极管连接。通过钻两个金属孔将超材料结构与两片地平面连接起来，用于输入偏置直流（DC）电压。单元的总尺寸为$6\times 6\times 2{mm}^3$，在中心频率处约为$0.172\times 0.172\times 0.057{\lambda }^3$。偏置二极管可以用直流电压控制。当偏置电压为3.3V时，二极管处于“ON”状态，相应的有效电路如图S5(a)所示；当无偏压时，二极管处于“OFF”状态，相应的电路模型如图S5(b)所示。在CST Microwave Studio中导入电路模型，得到的数值仿真结果表明，当二极管处于导通状态时，超材料单元表现为“1”编码，当二极管处于关闭状态时，超材料单元表现为“0”编码。如图6(b)所示，在8.3-8.9 GHz频段，相位差约为180°。在8.6 GHz时，相位差正好是180°。
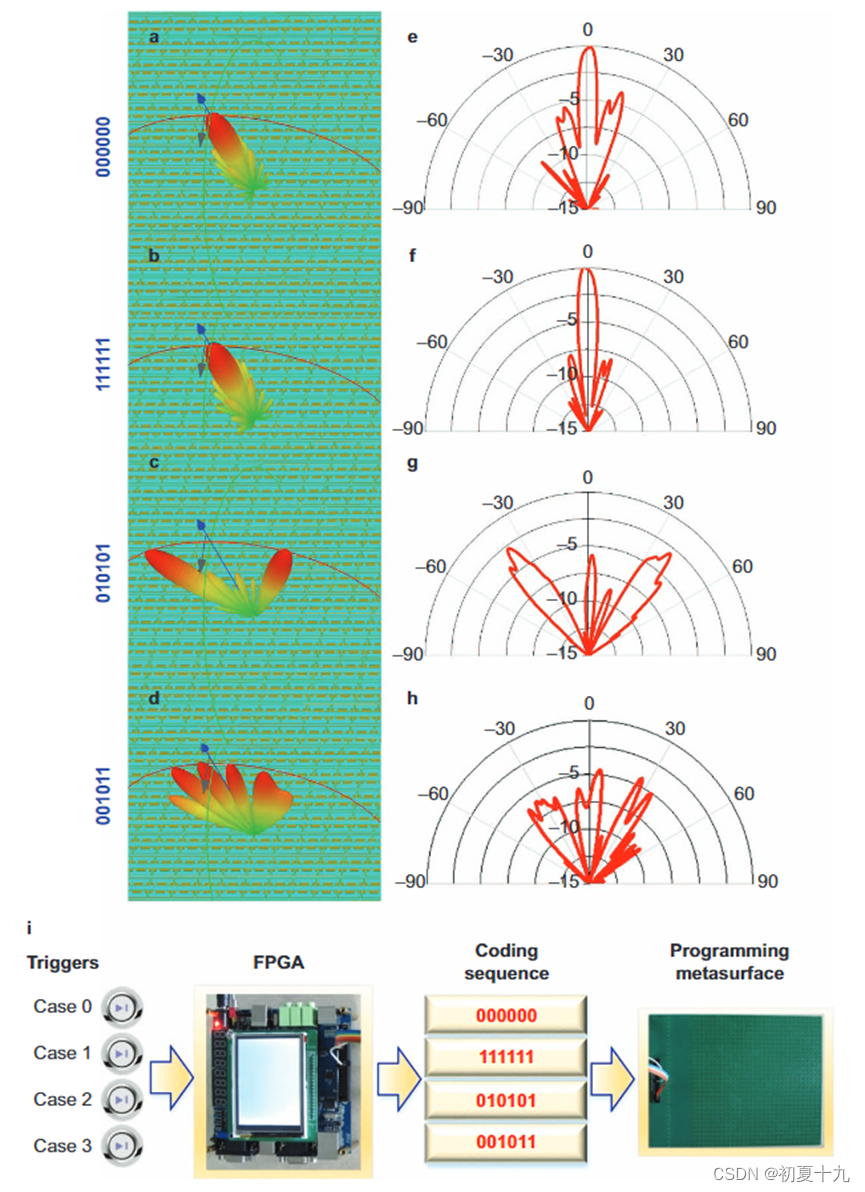
  基于超材料单元，我们设计并制作了一个1位数字超表面样本，如图补充图S6(a)、S6©和S6(d)所示。数字超表面包含30×30个相同的单元格，在每个单元中有一个偏置二极管（补充图S6(d)）。每五个相邻列的单元共享一个控制电压，对应于控制字的单个比特。因此，这是一个一维（1D）数字超表面，编码序列有六个控制字。作为示例，我们选择四个编码序列来验证上述概念：000000、111111、010101和001011。一维数字超表面的三维散射图仿真结果分别如图7(a)-7(d)所示。如图7(a)-7(d)所示，当编码序列为000000和111111时正常入射的波束被原路反射回去，因为它们完美地模拟了电导体和磁导体。当编码序列为周期序列010101时，超表面将正常入射的波束向两个主要的方向反射出去，如图7©所示。当编码序列为一般序列001011时，入射波束被散射成多个RCS值较低的波束，如图7(d)所示。

可编程超材料

  为了对编码序列进行数字控制，我们设计并实现了FPGA硬件，如补充图S6(b)所示。使用四个开关作为触发器，控制产生不同的编码序列。当一个开关被拨动时，FPGA将输出相应的编码序列。因此，我们可以通过切换不同的触发器以数字方式改变超表面上的电压分布，电压分布进一步控制偏置二极管的“ON”和“OFF”状态，从而产生数字超表面所需的所有“0”和“1”编码。因此，这种特殊的超表面拥有FPGA程序控制下的不同功能，从而实现可编程超表面。由FPGA触发的可编程超表面流程图如图7(i)所示。实验验证了单一超表面操纵电磁波的多种能力。FPGA产生编码序列000000、111111、010101和001011并得到一维数字超表面的实测散射模式如图7(e)-(h)所示，从这些图中，我们清楚地观察到多种不同的功能，这与图7(a)-(d)中所示的数值仿真很好地一致。

结论

  本文中，我们提出了编码超材料、数字超材料和可编程超材料的概念，给出了这些超材料的设计和实现，并使用超材料进行了相关实验验证。编码超材料仅由两种类型的单元组成，具有0和\pi相位响应，我们将其定义为“0”和“1”编码。通过控制序列编码“0”和“1”（即1位编码），我们可以操纵电磁波并实现不同的功能。编码超材料的概念可以从1位编码扩展到2位或更高位的编码。在2位编码中，需要使用具有四种类型的单元，其相位响应分别为$0$、$\pi /2$、$\pi$和$3\pi /2$，分别模拟“00”、“01”、“10”和“11”编码。相比1位编码超材料，2位编码超材料在调控电磁波时具有更大的自由性。
  我们还提出了一种独特的平面亚波长超材料单元结构，通过偏置二极管的控制，可以实现“0”和“1”编码。基于这种新型的超材料单元，我们设计并实现了一种数字超材料，其中每个元件都具有受偏置直流电压控制的“0”和“1”状态。我们构建了FPGA硬件来控制编码序列的产生，并将其输入到数字超材料中。因此，可以通过编写FPGA程序控制单个数字超材料来获得不同的电磁波操纵能力，从而实现了可编程超材料。
  所提出的编码超材料、数字超材料和可编程超材料对于控制天线的辐射波束（类似于相控阵天线，但使用不同的原理和成本极低的方法）、减少目标的散射特征和实现其他智能超材料等各种应用都非常有吸引力。所提出的工作可以扩展到毫米波和太赫兹频段。