MATLAB(simulink仿真)-PMSM电机模型-SVPWM-PI电流环-PI转速环的简易搭建

PMSM电机模型搭建

双击左键，搜索per（Permanent Magnet Synchronous Machine），第一个为PMSM电机模型

PMSM的电机模型中Tm为负载，ABC为三相线，m为电机内部的一些信息。

 提取m中的信息，通过Bus Selector模块来提取，选取电机信息（双击Bus Selector模块）：ABC相电流，转速，机械角度，转矩

注：机械角度指的是转子相对于定子旋转的实际空间角度，这是肉眼可见的角度。在无刷直流电机（BLDC）的FOC（磁场定向控制）中，Park变换就是使用电角度来进行的。这是因为在电机控制中，电角度能够准确地描述电动势和电流的变化周期，从而实现更精确的控制。

电角度与机械角度的关系可以用以下公式表示： 电角度 = 极对数 × 机械角度

 进行电机内部参数选择，电阻，电感，磁链，电机惯量J，摩擦系数，极对数等

 将机械角度进行转换--电角度*4，对电角度进行取余处理可以更直观的看到转了多少圈-选取常数模块（constant），取余模块（mod）-对2*pi进行取余即可；

转速由rad/s转化为rad/min----*60/（2*pi），MUX模块多接一；

SVPWM模块的搭建

选取逆变桥模块（Universal Bridge），并对其进行设置，选取IGBT，右键单击模块-格式-翻转模块-左/右；

左边为母线电压-选取DC Voltage Source，配置母线电压的值-311V；再加上接地-Ground。添加powergui模块。

选取SVPWM模块，配置参数--控制周期5000，matlab自带的SVPWM模块没有母线电压（这是一个标幺化的值），在dq与Alpha-Beta间加上一个增益（sqrt（3）/311）来解除 

选取反park变换模块（dq to Alpha-Beta-Zero），dq处用MUX引出3个，demux模块引出；wt周期部分，常数模块（constant），积分模块（Integrator）；dq轴直接给定制

注：在模型复杂后，仿真会变慢，修改建模-模型设置-求解器类型修改为定步长，求解器-ode3；步长<采样周期<控制周期 且最好是整数倍关系；

        注：封装技巧---以增益为例

选中增益，按住ctrl+G ；就将其进行了一个封装；

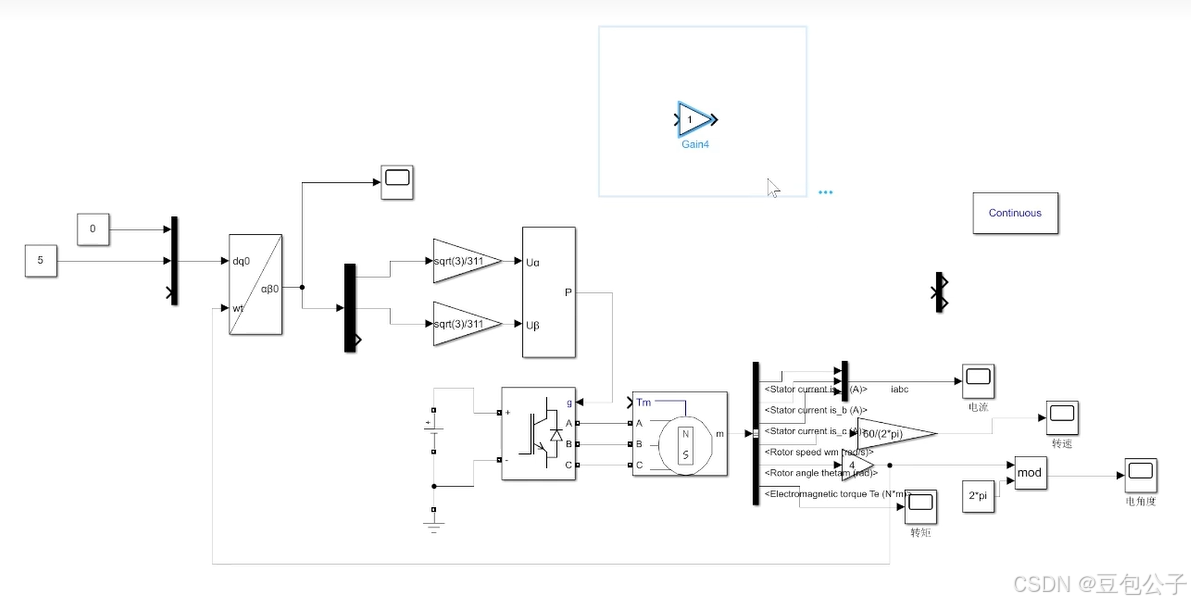
电流环的搭建

  添加PID模块（PID Controller）；选择pi，KP,KI暂时不设置，设置输出饱和-进行限幅输出-311/sqrt（3），与母线电压有关

再添加一个SUM模块，作为给定信号与反馈信号的一个比较器；添加park模块（abc to dp），翻转一下（快捷键-ctrl+r-翻转90°），添加一个转矩常数-暂时给0，连接各个信号，ID=0,IQ=2;

调节KP=50,KI=2000（随便调）,仿真时间加到2s，进行仿真调试；可以看到，转速到达一定后，就平稳，上不去了---由于电压已近到达一个限幅值，要再大就要进入非线性调节的区域了；电流IQ可以看到，由于电压被反电动势拉了下去，IQ也起不来了。

转速环的添加

        再添加一个PID模块，转速给500（其单位取决于反馈速度的单位），并对其PID进行限流（10A），KP=0.5,KI=10（大概的调一下，主要是实现整体架构）;后续再对各个模块实现的原理与参数的选取进行说明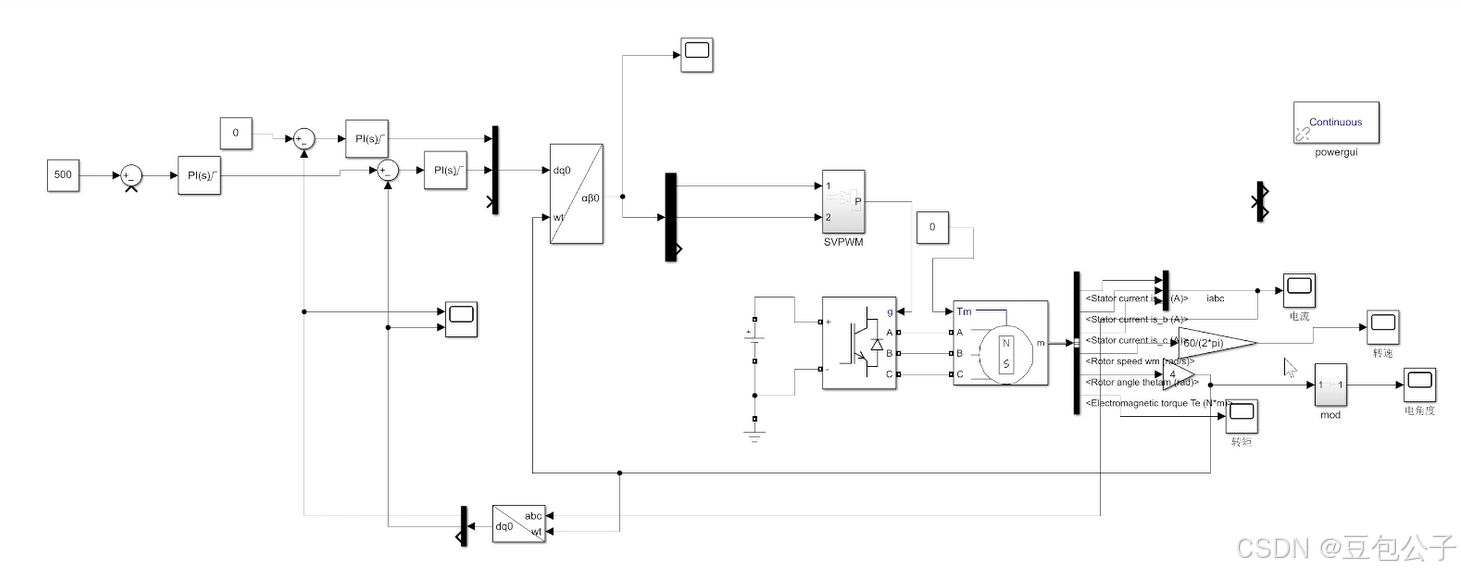

补充：

提取信息模块：Bus Selector模块来提取

合成信息：