支持向量机——JMU作业

最新推荐文章于 2024-07-09 16:57:56 发布

Heimdall.

最新推荐文章于 2024-07-09 16:57:56 发布

阅读量711

点赞数 17

文章标签：支持向量机算法机器学习

本文链接：https://blog.csdn.net/weixin_60732906/article/details/135374804

版权

本文介绍了支持向量机的基本概念、分类方法（包括线性可分、软间隔和硬间隔）、核函数的应用以及在鸢尾花数据集上的分类预测，包括线性SVM和RBF非线性SVM的模型构建、参数调优和性能评估。通过实例展示了如何使用SVM进行数据分类和模型优化。

摘要由CSDN通过智能技术生成

三、实验步骤——基于SVM实现鸢尾花分类预测

四、总结

一、概述

1.1 支持向量机的定义：

支持向量机（support vector machines，SVM）是一种分类模型，其基本定义为特征空间上的间隔最大化的线性分类器，本质上是一个求解凸二次规划的问题。

支持向量机是求解特征空间上的最大间隔（软间隔、硬间隔），是一个线性分类器，为了支持非线性的分类，引入了核技巧，用于将输入从输入空间映射到特征空间。相比较而言，核变换方法算是比支持向量机用得更广泛的一种机器学习方法。

1.2 基本思想

1.寻找最优的超平面：SVM 的目标是在特征空间中找到一个最优的超平面，以能够将不同类别的样本正确地分开。超平面是一个 d-1 维的子空间，其中 d 是特征空间的维度。

2.最大化间隔：SVM 在寻找超平面时，会尽可能地将不同类别的样本分开，并且使得支持向量（离超平面最近的样本点）到超平面的距离最大化。这个距离被称为间隔（margin），因此 SVM 也被称为最大间隔分类器。

3.核函数技巧：当样本数据线性不可分时，SVM 通过引入核函数来将数据映射到高维特征空间，从而使得非线性问题在高维空间中变得线性可分。常用的核函数有线性核、多项式核、高斯径向基函数（RBF）核等。

4.支持向量：在 SVM 中，只有少数关键的样本点对确定超平面起作用，这些样本点被称为支持向量。SVM 的决策边界只与支持向量有关，而与其他样本点无关，这也是 SVM 算法高效的原因之一。

5.正则化参数 C：SVM 中的正则化参数 C 控制了模型的复杂度与容错能力之间的权衡。较小的 C 值会使得分类器更加允许出现错误分类，使得决策边界更加平滑；而较大的 C 值会强制分类器尽可能正确分类所有样本，可能导致过拟合。

1.3 主要分类

线性可分支持向量机
线性支持向量机
非线性支持向量机

假设一个分类问题的输入空间于特征空间不同，则线性可分向量机和线性支持向量机假设这两个空间的元素可以一一对应，非线性支持向量机则利用一个非线性核技巧完成映射。支持向量机的学习都是基于特征空间进行的。

二、简介

2.1线性可分与线性不可分问题

在线性可分问题中，SVM 的目标是找到一个超平面，能够完全将不同类别的样本正确地分开。这意味着存在一个超平面，使得所有正样本都在超平面的一侧，而负样本都在另一侧。

数学上，对于一个线性可分的二分类问题，可以用以下形式的方程表示超平面：

$w^t*x+b=0$

其中，w 是法向量（normal vector）, x 是样本特征向量，b 是偏置（bias），w^T 表示向量 w 的转置与向量 x 的点积。

在线性可分问题中，可以通过求解一个凸优化问题来寻找最优的超平面。这个问题的目标是最大化间隔，并且要满足所有正样本和负样本的约束条件。

然而，实际应用中，许多问题并不是线性可分的，即使使用直线或平面也无法完全将不同类别的样本分开。这时候就需要引入一些方法来处理线性不可分问题。

一种常用的方法是引入松弛变量（slack variable），它允许样本出现错误分类。通过引入松弛变量，可以允许一些样本位于超平面的错误一侧，从而使得分类器具有容错能力。

线性不可分问题可以通过引入软间隔 SVM（Soft Margin SVM）来解决。软间隔 SVM 允许一些样本位于超平面的边界区域，同时尽可能地减小松弛变量的数量。这样可以在保持分类器简单性和泛化能力的同时，允许一些错误的分类。

另外，当线性不可分问题无法通过低维空间的超平面进行划分时，可以使用核函数。核函数可以将样本映射到高维特征空间，使得非线性问题在高维空间中变得线性可分。常用的核函数有线性核、多项式核、高斯径向基函数（RBF）核等。

2.2最大间隔与分类

当超平面（决策分界面）方程等于0的时候，x便是位于超平面上的点，而f(x)大于0的点对应 y=1 的数据点，f(x)小于0的点对应y=-1的点。也就是正样本在分隔超平面“上方”，负样本在分隔超平面”下方“。这也就意味着超平面函数需要等于0，SVM就是能将两类数据正确划分并且间隔最大的直线。

2.3软间隔与硬间隔

在SVM中，硬间隔（hard margin）和软间隔（soft margin）是用于处理线性不可分问题的两种方法。

硬间隔SVM只适用于线性可分问题，即存在一个超平面能够完全将不同类别的样本正确地分开。硬间隔SVM的目标是要找到一个最优的超平面，使得所有的样本都满足约束条件，即正样本位于超平面一侧，负样本位于另一侧，并且不存在任何样本位于超平面上或距离超平面非常接近。

然而，在实际问题中，很多数据集是线性不可分的，即无法通过一个超平面完全将不同类别的样本分开。这时就需要引入软间隔SVM。

软间隔SVM允许一些样本位于超平面的边界区域或错误分类。它通过引入松弛变量（slack variable）来实现容错能力。松弛变量表示了样本与其真实分类之间的误差程度，可以理解为对错误分类的惩罚项。软间隔SVM的目标是找到一个最优的超平面和最小化松弛变量，同时使得间隔尽可能大。

在软间隔SVM中，通过控制一个正则化参数C来平衡间隔的大小和错误分类的容忍度。较小的C值会允许更多的错误分类，使得决策边界更加平滑；而较大的C值会强制分类器尽可能正确分类所有样本，可能导致过拟合。

2.4拉格朗日乘子法

拉格朗日乘子法（Lagrange Multiplier Method）是一种用于求解约束最优化问题的数学方法。通过引入拉格朗日乘子，将约束条件融入目标函数中，从而将原始问题转化为一个无约束的优化问题。

假设我们要求解如下形式的最优化问题：

最小化（或最大化）目标函数 f(x)，满足约束条件 g(x) = 0。

其中，x 是待求解的变量。

为了使用拉格朗日乘子法求解这个问题，我们引入一个拉格朗日乘子 λ，构建拉格朗日函数：

L(x, λ) = f(x) + λg(x)。

然后，我们可以将原始问题转化为一个无约束的优化问题，即求解拉格朗日函数 L(x, λ) 的极值问题：

最小化（或最大化）L(x, λ)。

为了找到 L(x, λ) 的极值点，我们需要对 x 和 λ 分别求导，并令导数等于零：

∂L(x, λ)/∂x = 0， ∂L(x, λ)/∂λ = 0。

通过求解这个方程组，我们可以得到关于 x 和 λ 的解。其中，x 就是原始问题的最优解，而 λ 则对应着约束条件的乘子。

2.5核函数

基本思想：

SVM核函数是用于处理非线性问题的一种技术。其基本思想是将低维输入空间中的样本通过非线性映射转换到高维特征空间，使得在高维特征空间中的样本可以通过线性超平面进行有效的分割。

核函数的作用是在不显式计算高维特征空间的情况下，隐式地将样本映射到高维空间。这样可以避免直接计算高维特征空间的复杂性，而只需要在低维空间中进行计算。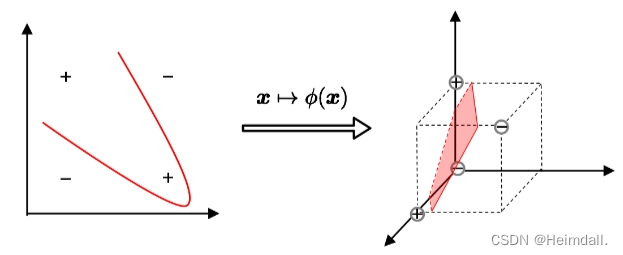

三、实验步骤——基于SVM实现鸢尾花分类预测

import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score
 
 
# 导入数据，分离特征与输出
iris = load_iris()
iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)
target = pd.Series(iris.target)
print('特征和目标的大小', iris_df.shape, target.shape)
 
# 画布属性设置
mpl.rcParams['font.family'] = ['sans-serif']
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
 
# 散点图
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
scatter = plt.scatter(iris_df.iloc[:, 0], iris_df.iloc[:, 1], c=target, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('鸢尾花特征分析散点图')
a, b = scatter.legend_elements()
print('散点对象及其标签', a, b)
b = ['setosa', 'versicolor', 'virginica']  # 原标签0，1，2分别对应以下三种
plt.legend(a, b)
 
plt.subplot(1, 2, 2)
scatter = plt.scatter(iris_df.iloc[:, 2], iris_df.iloc[:, 3], c=target, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('鸢尾花特征分析散点图')
a, b = scatter.legend_elements()
print('散点对象及其标签', a, b)
b = ['setosa', 'versicolor', 'virginica']  # 原标签0，1，2分别对应以下三种
plt.legend(a, b)
plt.show()
 
# 划分训练和测试数据
X_train, X_test, y_train, y_test = train_test_split(iris_df, target, test_size=0.2, random_state=5)
 
# 线型SVM模型训练
linear_svm = SVC(kernel='linear', C=1, random_state=0)
linear_svm.fit(X_train, y_train)
 
# 基于RBF非线性SVM模型训练
rbf_svm = SVC(kernel='rbf', C=1, gamma=0.1, random_state=0)
rbf_svm.fit(X_train, y_train)
 
# 模型评估
linear_y_pred = linear_svm.predict(X_test)
linear_accuracy = accuracy_score(y_test, linear_y_pred)
 
rbf_y_pred = rbf_svm.predict(X_test)
rbf_accuracy = accuracy_score(y_test, rbf_y_pred)
 
print()
print('线性SVM模型模型评估：')
print('参数C:', linear_svm.C)
print('分类准确度accuracy: ', linear_accuracy)
print()
print('RBF非线性SVM模型评估：')
print('参数C:{:d},gamma:{:.1f}'.format(rbf_svm.C, rbf_svm.gamma))
print('分类准确度accuracy: ', rbf_accuracy)
 
# print('真实分类：', list(y_test))
# print('预测分类', list(linear_y_pred))
 
 
# 线型模型分类结果展示
plt.figure(figsize=(8, 8))
plt.subplot(2, 2, 1)
plt.scatter(X_test.iloc[:, 0], X_test.iloc[:, 1], c=y_test, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('真实散点图')
plt.subplot(2, 2, 2)
plt.scatter(X_test.iloc[:, 0], X_test.iloc[:, 1], c=linear_y_pred, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('预测散点图')
plt.subplot(2, 2, 3)
plt.scatter(X_test.iloc[:, 2], X_test.iloc[:, 3], c=y_test, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('真实散点图')
plt.subplot(2, 2, 4)
plt.scatter(X_test.iloc[:, 2], X_test.iloc[:, 3], c=linear_y_pred, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('预测散点图')
plt.suptitle('线性模型分类结果对照图')
plt.show()
 
# rbf非线型模型分类结果展示
plt.figure(figsize=(8, 8))
plt.subplot(2, 2, 1)
plt.scatter(X_test.iloc[:, 0], X_test.iloc[:, 1], c=y_test, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('真实散点图')
plt.subplot(2, 2, 2)
plt.scatter(X_test.iloc[:, 0], X_test.iloc[:, 1], c=rbf_y_pred, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('预测散点图')
plt.subplot(2, 2, 3)
plt.scatter(X_test.iloc[:, 2], X_test.iloc[:, 3], c=y_test, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('真实散点图')
plt.subplot(2, 2, 4)
plt.scatter(X_test.iloc[:, 2], X_test.iloc[:, 3], c=rbf_y_pred, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('预测散点图')
plt.suptitle('rbf非线性模型分类结果对照图')
plt.show()
 
# 参数调优
print()
print('模型调优')
linear_params = {'C': [0.1, 0.5, 1, 5, 10]}
linear_gridsearch = GridSearchCV(SVC(kernel='linear'), linear_params, scoring='accuracy', cv=5)
linear_gridsearch.fit(X_train, y_train)
print('线性SVM参数调优结果：', linear_gridsearch.best_params_)
linear_svm.C = linear_gridsearch.best_params_['C']
 
rbf_params = {'C': [0.1, 0.5, 1, 5, 10], 'gamma': [0.001, 0.01, 0.1, 1, 10]}
rbf_gridsearch = GridSearchCV(SVC(kernel='rbf'), rbf_params, cv=5)
rbf_gridsearch.fit(X_train, y_train)
print('RBF非线性SVM参数调优结果：', rbf_gridsearch.best_params_)
rbf_svm.C = rbf_gridsearch.best_params_['C']
rbf_svm.gamma = rbf_gridsearch.best_params_['gamma']
 
# 模型评估
linear_y_pred = linear_svm.predict(X_test)
linear_accuracy = accuracy_score(y_test, linear_y_pred)
 
rbf_y_pred = rbf_svm.predict(X_test)
rbf_accuracy = accuracy_score(y_test, rbf_y_pred)
 
print()
print('参数调优后的模型性能：')
print('C:', linear_svm.C)
print('线性SVM模型准分类确度: ', linear_accuracy)
print('C,gamma:', rbf_svm.C, rbf_svm.gamma)
print('RBF非线性SVM模型准分类确度:  ', rbf_accuracy)

四、总结

本次实验主要是使用SVM模型对鸢尾花数据集进行分类，并使用可视化的方法展示训练集、测试集和决策边界的情况。

首先，通过加载数据集得到特征向量X和目标变量y，并将其划分为训练集和测试集（70%的数据作为训练集）。

然后，定义了一个SVM模型，使用径向基函数核（kernel='rbf'）并设置C=1.0。径向基函数核常用于处理非线性问题，并且具有一定的容错能力。同时，C参数控制了模型的错分惩罚，C越大则惩罚越强，可能会导致过拟合。

接下来，使用plot_scatter函数可视化训练集，其中按照目标变量y的不同取值对应不同的颜色和标记。同时，通过legend函数添加图例，方便展示。

最后，使用plot_decision_boundary函数可视化测试集和决策边界。该函数首先根据X的范围定义了网格点的坐标，然后使用SVM模型进行预测，得到对应的决策边界。最后，将预测结果和测试集的实际取值进行比较，并绘制出来。其中，plt.contourf函数用于绘制等高线区域，由于SVM分类是一个二分类问题，因此使用cmap=plt.cm.Paired来指定颜色映射。

在实验中数据集不平衡：如果训练集和测试集中的样本数量差异较大，可能会导致模型的性能下降。因此，在实验中需要进行合理的样本划分和调整，以保证数据集的平衡性。

Heimdall.

关注

17
点赞
踩
21

收藏

觉得还不错? 一键收藏
1
评论
支持向量机——JMU作业

支持向量机（support vector machines，SVM）是一种分类模型，其基本定义为特征空间上的间隔最大化的线性分类器，本质上是一个求解凸二次规划的问题。支持向量机是求解特征空间上的最大间隔（软间隔、硬间隔），是一个线性分类器，为了支持非线性的分类，引入了核技巧，用于将输入从输入空间映射到特征空间。相比较而言，核变换方法算是比支持向量机用得更广泛的一种机器学习方法。在线性可分问题中，SVM 的目标是找到一个超平面，能够完全将不同类别的样本正确地分开。
复制链接

扫一扫