深度学习入门基于python的理论与实现-第三章神经网络（个人向笔记）

激活函数

激活函数是连接感知机和神经网络的桥梁

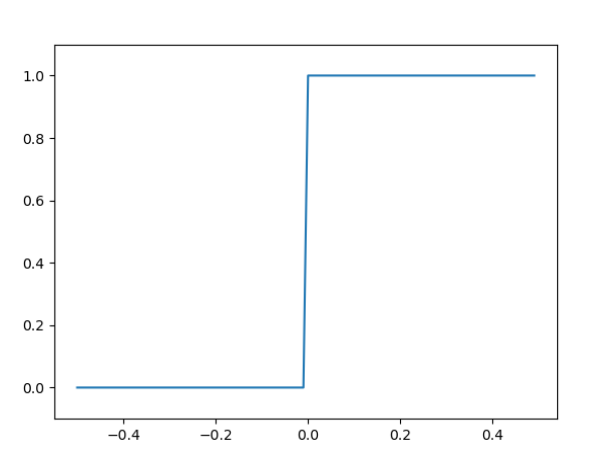
阶跃函数

阶跃函数是在感知机中使用的激活函数。
$$h(x)=\{\begin{array}{l}0x<0\\ 1x>=0\end{array}$$

图像：

实现

import numpy as np


def step_function(x):
    y = x > 0
    return y.astype(np.int)


print(step_function(np.array([1, -1, 1, 3, -3, -4])))

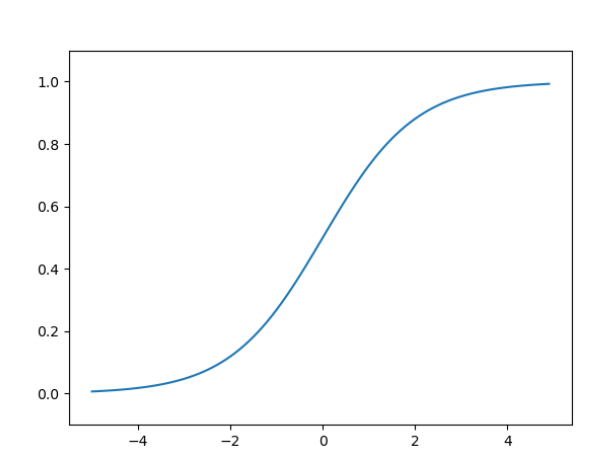
sigmoid函数

$$h(x)=\frac{1}{1+e^{-x}}$$
其中$e=\mathrm{2.7182...}$是纳皮尔常数。
图像：

实现

import numpy as np
import matplotlib.pyplot as plt


# numpy array具有广播功能
def sigmoid(x):
    return 1 / (1 + np.exp(-x))


# x = np.arange(-5, 5, 0.1)
# y = sigmoid(x)
# plt.plot(x, y)
# plt.ylim(-0.1, 1.1)
# plt.show()

在感知机中使用的是阶跃函数，在神经网络中我们引入了sigmoid函数。
可以先比较两种函数
从两方面去比较
不同点：

1. 平滑性：阶跃函数是不平滑的，sigmoid函数是平滑的
2. 返回值：阶跃函数只能返回两种值0|1，sigmoid可以返回的值是[0,1]之间的实数
   相同点：
3. 从宏观上去看，两者的趋势比较一致或者说形状吧
4. 两者均属于非线性函数

神经网络中的激活函数必须使用非线性函数。
为什么呢？
可以考虑使用线性函数，我们知道神经网络是一层一层这样叠加下去，使用线性函数的话，无论叠加多少层，到最后我们的函数都可以等价为只使用一个等价的线性函数

ReLU函数

h ( x ) = { 0 x < 0 x