目录
一.特殊矩阵
1.通用的特殊矩阵
1)zeros函数:产生全0矩阵,即零矩阵。
2)ones函数:产生全1矩阵,即幺矩阵。
3)eye函数:产生对角线为1的矩阵。当矩阵为方阵时,得到一个单位矩阵。
4)rand函数:产生(0,1)区间均匀分布的随机矩阵。
5)randn函数:产生均值为0,方差为1的标准正态分布随机矩阵。
zeros函数调用格式:
1)zeros(m):产生m*m零矩阵/
2)zeros(m,n):产生m*n零矩阵。
3)zeros(size(A)):产生与矩阵A同样大小的零矩阵。
>>A=zeros(2,3)
A=
0 0 0
0 0 0
>>zeros(size(reshape(A,3,2)))
ans=
0 0
0 0
0 0 %reshape函数:将A转换为3行两列;size函数:输出改变后A的行列数例1.首先产生5阶两位随机整数矩阵A,在产生均值为0.6,方差为0.1的5阶正态分布随机矩阵B,最后验证(A+B)I=IA+BI(I为单位矩阵)
a.rand函数:产生(0,1)开区间均匀分布的随机数x。
b.fix(a+(b-a+1)*x):产生[a,b]区间上均匀分布的随机整数。
c.randn函数:产生均值为0,方差为1的标准正态分布随机数x。
d.
:得到均值为
,方差为
的随机数。

rand函数取值范围小于1,如果不加上1就无法取到99
(1)randi : 产生均匀分布的随机整数(i = int)
产生一个1至10之间的随机整数矩阵,大小为2x5;
s1 = randi(10,2,5)
产生一个-5至5之间的随机整数矩阵,大小为1x10;
s2 = randi([-5,5],1,10)(2) rand: 产生0至1之间均匀分布的随机数
产生一个0至1之间的随机矩阵,大小为1x5;
s3 = rand(1,5)
产生一个a至b之间的随机矩阵,大小为1x5; % a + (b-a) * rand(1,5); 如:a,b = 2,5
s4= 2 + (5-2) * rand(1,5)(3)normrnd:产生正态分布的随机数
产生一个均值为0,标准差(方差开根号)为2的正态分布的随机矩阵,大小为3x4;
s5 = normrnd(0,2,3,4)(4)roundn—任意位置四舍五入
0个位 1十位 2百位 -1小数点后一位
a = 3.1415
roundn(a,-2) % ans = 3.1400
roundn(a,2) % ans = 0
a =31415
roundn(a,2) % ans = 31400
roundn(5.5,0) %6
roundn(5.5,1) %10
fix函数
用于取近于0的整数,可以去掉随机数产生的小数部分
B:产生均值为0.6,方差为0.1的5*5矩阵
C:产生5阶单位阵
2.用于专门学科的特殊矩阵
(1)魔方矩阵
n阶魔方阵由1,2,3——
共
个整数组成,且每行列以及主副对角线上各n个元素之和都相等。
n阶魔方阵每行每列元素之和为
.
例2.产生8阶魔方阵,求其每行每列元素之和。

(2)范德蒙矩阵
(3)希尔伯特矩阵
在matlab中生成n阶希尔伯特矩阵的函数为hilb(n).
>>format rat %设置输出格式为有理数
>>H=hilb(4) %4阶输出
H =
1 1/2 1/3 1/4
1/2 1/3 1/4 1/5
1/3 1/4 1/5 1/6
1/4 1/5 1/6 1/7 病态矩阵:
如果一个元素发生变化,整个矩阵和逆矩阵均会变化,病态程度与矩阵阶数相关,阶数越高,病态更加严重
(4)伴随矩阵
MATLAB使用compan(p)生成矩阵,其中p为一个多项式的系数向量,高次幂系数排在前,低次幂系数排在后。
例如生成多项式
的伴随矩阵
>> p=[1,-2,-5,6];
>> A=compan(p)
A =
2 5 -6
1 0 0
0 1 0 (5)帕斯卡矩阵
二.矩阵变换
1.对角阵
1)分类
(1)对角矩阵:只有对角线上有非0元素的矩阵。
(2)数量矩阵:对角线上的元素相等的对角矩阵。
(3)单位矩阵:对角线上的元素都为1的矩阵。
2)提取矩阵的对角元素
D = diag(v)返回包含主对角线上向量v的元素的对角矩阵。
D = diag(v,k)将向量v的元素放置在第k条对角线上。k=0表示主对角线,k>0位于主对角线上方,k<0位于主对角线下方。
3)构造对角阵
x = diag(A)返回A的主对角线元素的列向量。
x = diag(A,k)返回A的第k条对角线上元素的列向量。PS.用对角阵左乘一个矩阵时相当于对角阵的对角线第一个元素乘上该矩阵的第一行,以此类推(类似的当对列实施操作应右乘)
2.三角阵
1)上三角阵:矩阵的对角线以下元素全为0的矩阵。
U = triu(A)返回矩阵A的上三角部分。
U = triu(A,k)返回位于A的第 k 条对角线上以及该对角线上方的元素。2)下三角阵:对角线以上的元素全为0的矩阵。
L = tril(A)返回矩阵A的下三角部分。
L = tril(A,k)返回A的第 k 个对角线上以及该对角线下方的元素。
3.矩阵的转置
1)转置操作以矩阵形式切换行和列。它由单引号(.')表示。
2)共轭转置,其运算符为单引号('),它在转置的基础上还要取每个数的复共轭。
4.矩阵的旋转
B = rot90(A)将数组A逆时针旋转 90 度。对于多维数组,rot90在由第一个和第二个维度构成的平面中旋转。
B = rot90(A,k)将数组A按逆时针方向旋转k*90度,其中k是一个整数。
5.矩阵的翻转
B = flip(A)返回的数组B具有与A相同的大小,但元素顺序已反转。B中重新排序的维度取决于A的形状:
如果
A为向量,flip(A)将沿向量的长度方向反转元素顺序。如果
A为矩阵,flip(A)将反转每列元素的顺序。如果
A为 N 维数组,flip(A)将按A的大小值不等于1的首个维度上进行运算。
B = flip(A,dim)沿维度dim反转A中元素的顺序。例如,如果A为矩阵,flip(A,1)将反转每一列中的元素,flip(A,2)将反转每一行中的元素。
6.矩阵的求逆
1)对于一个方阵A,如果存在一个与其同阶的方阵B,使得AB=BA=E,则称B为A的逆矩阵,当然A也是B的逆矩阵
2)
Y = inv(X)计算方阵X的 逆矩阵。
X^(-1)等效于inv(X)。
x = A\b的计算方式与x = inv(A)*b不同,建议用于求解线性方程组。
三.矩阵求值
1.方阵的行列式
1)把一个方阵看作一个行列式,并对其按行列式的规则求值,这个值称为方阵所对应的行列式的值。
2)
d = det(A)返回方阵A的行列式。PS.det(A^-1)=1/det(A)
2.矩阵的秩
1)矩阵线性无关的行数或列数成为矩阵的秩。
2)
k = rank(A)返回矩阵A的秩。使用 sprank确定稀疏矩阵的结构秩。
k = rank(A,tol)指定在秩计算中使用另一个容差。秩计算为A中大于tol的奇异值的个数。PS.(1)奇数阶魔方阵秩为n,即奇数阶魔方矩阵为满秩矩阵。
(2)一重偶数阶魔方矩阵为n/2+2(n是2的倍数,非4的倍数)
(3)双重偶数阶魔方矩阵秩均为3(阶数为4的倍数)
3.矩阵的迹
1)矩阵的迹等有矩阵的对角线元素之和,也等于矩阵的特征值之和。
2)trace(A):求矩阵A的迹。
4.向量和矩阵的范数
n = norm(vv)返回向量v的欧几里得范数。此范数也称为 2-范数、向量模或欧几里德长度。
n = norm(v,p)返回广义向量 p-范数。
n = norm(X)返回矩阵X的 2-范数或最大奇异值,该值近似于max(svd(X))。
n = norm(X,p)返回矩阵X的 p-范数,其中p为1、2或Inf:
如果
p = 1,则n是矩阵的最大绝对列之和。如果
p = 2,则n近似于max(svd(X))。这相当于norm(X)。如果
p = Inf,则n是矩阵的最大绝对行之和。
n = norm(X,'fro')返回矩阵X的 Frobenius范数。
5.矩阵的条件数
1)矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积。
2)条件数越接近1,矩阵的性能越好,反之,矩阵的性能越差。
C = cond(A)
C = cond(A,p)
C = cond(A)returns the 2-norm condition number for inversion, equal to the ratio of the largest singular value ofAto the smallest.
C = cond(A,p)returns thep-norm condition number, wherepcan be1,2,Inf, or'fro'.
四.矩阵的特征值与特征向量
1.矩阵的特征值
设A是n阶方阵,如果数λ和n维非零列向量x使关系式Ax=λx成立,那么这样的数λ称为矩阵A特征值,非零向量x称为A的对应于特征值λ的特征向量。式Ax=λx也可写成( A-λE)X=0。这是n个未知数n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式| A-λE|=0。
2.求矩阵的特征值和特征向量
函数调用格式:
e = eig(A)
[V,D] = eig(A)
[V,D,W] = eig(A)
e = eig(A,B)
[V,D] = eig(A,B)
[V,D,W] = eig(A,B)
[___] = eig(A,balanceOption)
[___] = eig(A,B,algorithm)
[___] = eig(___,eigvalOption)
说明:
- e = eig(A) 返回一个列向量,其中包含方阵 A 的特征值。
- [X,D] = eig(A) 返回特征值的对角矩阵 D 和特征值的矩阵 X,其列是对应的右特征向量,使得 A*X(:,1) = D(1)*X(:,1)。
- [V,D,W] = eig(A) 还返回满矩阵 W,其列是对应的左特征向量,使得 W'*A = D*W'。 特征值问题是用来确定方程 Av = λv 的解,其中,A 是 n×n 矩阵,v 是长度 n 的列向量,λ 是标量。满足方程的 λ 的值即特征值。满足方程的 v 的对应值即右特征向量。左特征向量 w 满足方程 w’A = λw’。
- e = eig(A,B) 返回一个列向量,其中包含方阵 A 和 B 的广义特征值。
- [V,D] = eig(A,B) 返回广义特征值的对角矩阵 D 和满矩阵 V,其列是对应的右特征向量,使得 A*V = B*V*D。
- [___] = eig(A,balanceOption)(其中,balanceOption 为 'nobalance')禁用该算法中的初始均衡步骤。balanceOption 的默认值是 'balance',表示启用均衡步骤。eig 函数可以返回先前语法中的任何输出参数。
- [___] = eig(A,B,algorithm)(其中,algorithm 为 'chol')使用 B 的 Cholesky 分解计算广义特征值。algorithm 的默认值取决于 A 和 B 的属性,但通常是 'qz',表示使用 QZ 算法。
- 如果 A 为 Hermitian 并且 B 为 Hermitian 正定矩阵,则 algorithm 的默认值为 'chol'。
- [___] = eig(___,eigvalOption) 使用先前语法中的任何输入或输出以 eigvalOption 指定的形式返回特征值。将 eigvalOption 指定为 'vector' 可返回列向量中的特征值,指定为 'matrix' 可返回对角矩阵中的特征值。
3.特征值的几何意义
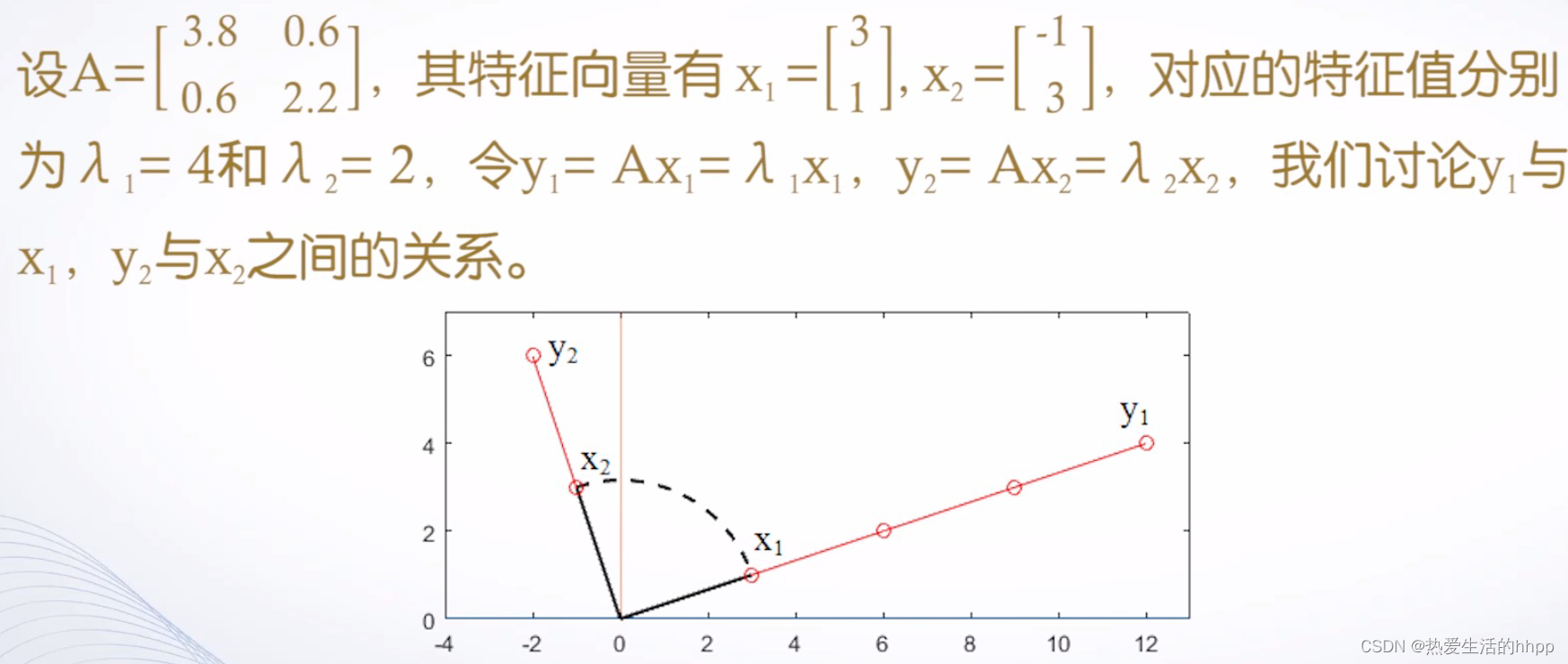
y1和y2是由x1和x2变换而来,A为变换矩阵,
为伸缩因子
五.稀疏矩阵
零元素的个数远远多于非零元素的矩阵,为了减少内存消耗,我们选择减少0的存储
1.矩阵的存储方式
- 完全存储:将所有元素按列存储
- 稀疏存储:只存储矩阵的非零元素的值以及位置,即行号和列号
2.稀疏矩阵存储方式的产生
- 完全存储方式与稀疏存储方式的转化
A=sparse(S): 将矩阵S转化为稀疏存储方式的矩阵A。 S=full(A): 将矩阵A转化为完全存储方式矩阵S
- 直接建立稀疏存储矩阵
sparse(m,n): 生成一个m*n的所有元素都是零的稀疏矩阵 sparse(u,v,S): 其中u,v,S是三个登场的向量。S是要建立的稀疏存储矩阵的非零元素,u(i),v(i)分别是S(i)的行和列下标 B=spconvert(A) A为一个m*3或m*4的矩阵,其每行表示一个非零元素,m是非零元素的个数 A(i,1)表示第i个非零元素所在行 A(i,2)表示第i个非零元素所在列 A(i,3)表示第i个非零元素值的实部 A(i,4)表示第i个非零元素值的虚部
3.带状稀疏矩阵的稀疏存储
- 稀疏矩阵有两种基本类型:无规则结构的稀疏矩阵与有规则结构的稀疏矩阵
- 带状稀疏矩阵是指所有非零元素集中在对角线上的矩阵
[B,d] = spdiags(A) : 从带状稀疏矩阵A中提取全部非零对角线元素赋给矩阵B及其这些非零对角线的位置向量d。 A = spdiags(B,d,m,n): 产生带状稀疏矩阵的稀疏存储矩阵A,其中m,n为原带状系数矩阵的行数和列数,矩阵B的第i列即为原带状稀疏矩阵的第i条非零对角线,向量d为原带状稀疏矩阵所有非零对角线的位置
- 单位矩阵的稀疏存储:speye (m,n)返回一个m*n的系数存储单位矩阵
六.对矩阵的处理
(1)分析矩阵中的数据
any(a > 0.3) %%每一个列向量是否存在一个数大于0.3 all(a > 0.3) %%每一个列向量是否均大于0.3(2)寻找矩阵变化的位置
diff: 将相邻两位做差
































 599
599











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








