考研数学二 2011-2024年 真题积累总结【数列与导数篇】_单调有界准则_导数定义_二阶导数

数列

1.单调有界准则+积分的拆分

在本题中，核心的一点是，通过积分的拆分变形得出a_n的单调性，然后思考单调有界准则，考虑有界性。

题目来源:2025李林六套卷 卷1 选择7

2 单调有界准则

2013年 单调有界准则

思路:这道题问的是数列{a_n}收敛，又有有界。思路肯定是用单调有界准则

题目来源:2012年 数学二 3题

2024年 单调有界准则

3.1单调有界准则 证明题

3.1.1 2012年单调有界准则证明大题

难在第二问这种抽象的难以捋清思路

有且仅有一个实根---->零点定理+单调性
零点定理：f(a)f(b)<0,则说明f(a)和f(b)异号，存在一个f( c )在a到b之间，使得f( c )=0，一般来说取的这两点都是端点。
有且仅有也就是单调性，a到b之间是单调的，也就是说有且仅有一个实根

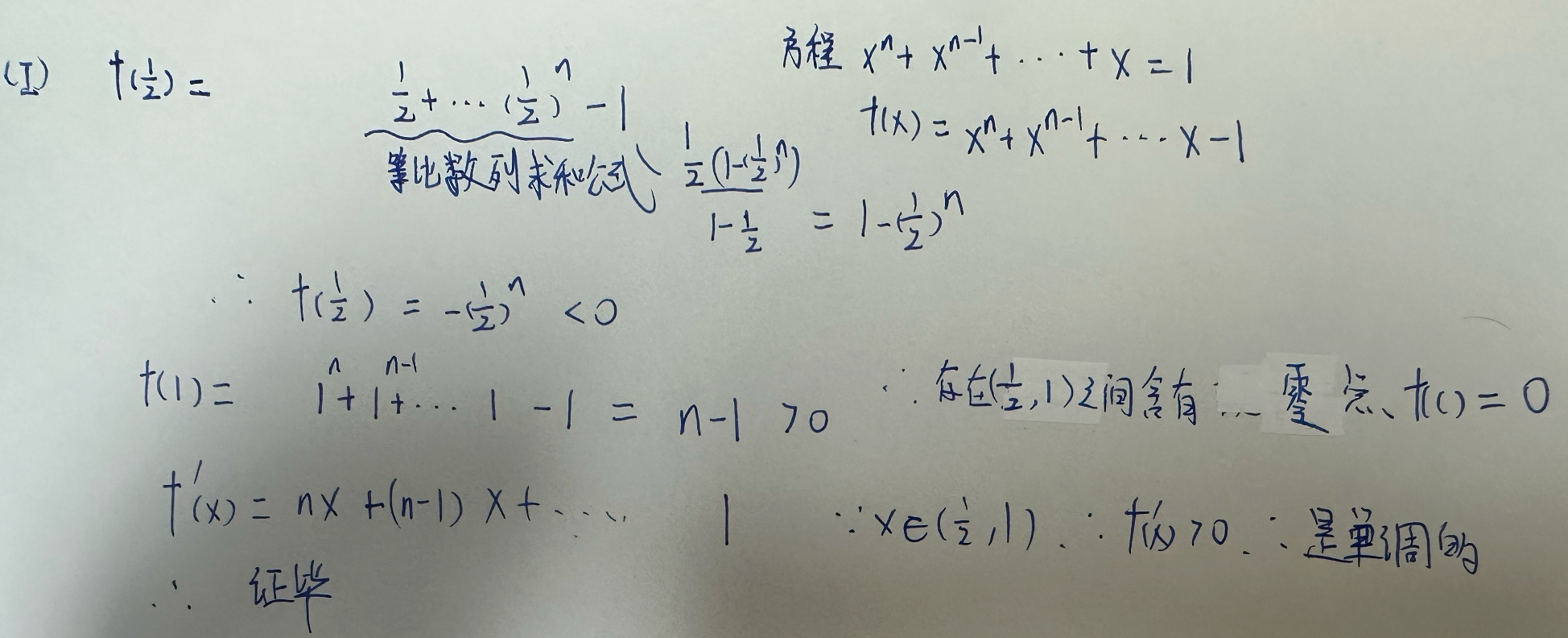
一般这种抽象的数列极限证明存在，都是用单调有界准则

3.1.2 2013年单调有界准则证明大题

本题中给的条件是一个不等式，而不是一个递推数列的形式，故用预求的方法，或是数学归纳法都不行。这种题的思路，其实是比较简单的，用数列的单调有界准则，无非是证明x_n<啥或>啥，单调性 无非是x_n-<x_n+1或x_n->x_n+1,根据给出的不等式和第一问中得到的结论的不等式，向这两个目的前进。

在最终计算极限的过程中，由于给的是不等式，想要求值，肯定要是等式才能求值，所以就是再找一个不等式，一个大于等于，一个小于等于，夹到=号成立，计算值。

导数

1.高阶导数的计算 牛顿莱布尼兹 泰勒公式

题目来源:2015年 数学二 第10题

2. 曲率相关（待更新）

2.1 2024 曲率圆

3.给出x趋近于0，实则求x趋近于1判断某点是否为驻点，是否为极值点

驻点就是该点的导数值是否为0
极值点这里用的脱帽法，已知某点在该点上=0，在邻域上>0，即可得到该点是极小值，周围的值都比它大

题目来源:2025李林六套卷 卷2 选择4

4.某点处导数定义和二阶导数定义

题目来源:2025李林六套卷 卷2 选择5

5.可导的定义，含有绝对值

可导的定义：

6.选择题排除法技巧或泰勒公式不等式证明

7. 实际应用转换数学模型，积分学与微分学的结合

8. 微积分可导连续

9.参数方程转化为直角坐标系下的方程，函数连续性，可导性判断

如何将参数方程转化为直角坐标系下的方程：
核心：用参数方程其中一个方程把参数表示出来，然后代入进另一个参数方程中

判断连续性，极限值是否=函数值
判断导数存在性，左导数是否=右导数，间断点用导数定义判断。