概率论与数理统计学习：随机事件（二）——知识总结与C语言实现案例

Hello，大家好。

这是第二期概率论与数理统计的学习，我将用这篇博客来整理我所学习的内容，及用C语言去做例题的过程。

那么话不多说，先梳理一下这期的知识点👇：

💦 条件概率

啥是条件概率？

把它分开读就是，“有条件的概率”，也就是这个概率有前提条件。

$P(A|B)$：读作在事件B发生的条件下，事件A发生的条件概率。

☁️ 相关性质

设A和B是两个事件，且$P(B)>0$,则称$$P(A|B)=\frac{P(AB)}{P(B)}$$
为在事件B发生的条件下，事件A发生的概率。同时，条件概率也叫概率，那么它应该满足概率定义的三个条件，即👇：

🌱 对每个事件A，均有$P(A|B)\ge 0$

🌱 $P(\Omega |B)=1$

🌱 若$A_1,A_2,\cdot \cdot \cdot$是两两互斥事件，则有$$P((A_1\cup A_2\cup \cdot \cdot \cdot )|B)=P(A_1|B)+P(A_2|B)+\cdot \cdot \cdot$$

因为条件概率也是概率，所以概率的所有性质，也都适用于条件概率。例如👇：$$P((A_1\cup A_2)|B)=P(A_1|B)+P(A_2|B)-P(A_1{A}_2|B)$$

☁️ 乘法公式

设A和B是两个事件，由前面☝️条件概率的定义可以知道，若$P(B)>0$，有$$P(AB)=P(B)\cdot P(A|B)$$
同理，当$P(A)>0$时，有$$P(AB)=P(A)\cdot P(B|A)$$
那么推广到多个事件的情况，有$$P(A_1{A}_2\cdot \cdot \cdot A_n=P(A_1)\cdot P(A_2|A_1)\cdot P(A_3|A_1{A}_2)\cdot \cdot \cdot P(A_n|A_1{A}_2\cdot \cdot \cdot A_{n-1})$$

☁️ 全概率公式

在学习全概率公式之前，我们需要引入样本空间划分的概念。

设$\Omega$为试验$E$的样本空间，$B_1,B_2,\cdot \cdot \cdot ,B_n$为一组事件，若$B_1,B_2,\cdot \cdot \cdot ,B_n$两两互斥，且$B_1\cup B_2\cup \cdot \cdot \cdot \cup B_n=\Omega$，则称$B_1,B_2,\cdot \cdot \cdot ,B_n$为样本空间$\Omega$的一个划分。例如👇：

图上的缝隙就请大家忽略哈（这个图在WPS我也没法继续搞了）

那么在引入了样本空间划分的概念后，我们就可以给出全概率公式了，设A为一个事件，$B_1,B_2,\cdot \cdot \cdot ,B_n$为$\Omega$的一个划分。👇：$$P(A)=\sum _{i=1}^{n}P(B_i)P(A|B_i)$$

☁️ 贝叶斯公式

设$\Omega$是样本空间，A为一个事件，$B_1,B_2,\cdot \cdot \cdot ,B_n$为$\Omega$的一个划分，且$P(A)>0$，$P(B_i)>0，i=1,2,...,n$，则👇：$$P(B_i|A)=\frac{P(B_i)P(A|B_i)}{{\sum }_{j=1}^{n}P(B_j)P(A|B_i)}$$

仔细一看就会发现，该分式的分子是乘法公式，分母就是全概率公式。关于乘法公式、全概率公式和贝叶斯公式的关系会在后续做题中逐步总结。

💦 事件的独立性

设A和B为两个事件，由条件概率可知，$P(A|B)$表示在事件B发生的条件下，事件A发生的概率；$P(A)$表示不管事件B发生与否，事件A发生的概率。

那么，若$P(A|B)=P(A)$，则表示事件B的发生并不影响事件A发生的概率，这时称事件A和B相互独立。那么乘法公式就可以写成如下公式👇：$$P(AB)=P(A|B)P(B)=P(A)P(B)$$，所以这个公式就可以用来表示事件的独立性。

所以，若$P(AB)=P(A)P(B)$成立，则称事件A与B相互独立。

❗️：在实际应用中，两个事件是否相互独立，是根据这两个事件的发生是否相互影响来判断的。例如：甲乙两人向同一目标射击，彼此互不相干，那么甲乙两人是否击中目标这两事件是相互独立的。

☁️ 定理

若事件A与B相互独立，则$A$与$\overline{B}$、$\overline{A}$与$B$、$\overline{A}$与$\overline{B}$也都相互独立。

关于事件的独立性，也可推广到多个事件的情况。这里就不再叙述了噢。

下面开始用C语言实现例题！

🌊 C语言案例实现

1. 有外观相同的三极管6只，4只属于甲类，2只属于乙类。不放回地抽取三极管两次，每次只抽一只，求在第一次抽到是甲类三极管的条件，第二次又抽到甲类三极管的概率。

设$A_i=$ {第$i$次抽到甲类三极管}，$i=1,2$。

#include <stdio.h>
int Combination(int n,int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}
	return sum/p;
}

void Abbreviation(long int *a)
{
	while(a[0] % 2 == 0 && a[1] % 2 == 0)
	{
		a[0] /= 2;
		a[1] /= 2;
	}
	for(int i = 3 ;i < a[1] / 2 ; i += 2)
	{
		while(a[0] % i == 0 && a[1] % i == 0)
		{
			a[0] /= i;
			a[1] /= i;
		}
	}
}

int main()
{
	// use A1 to denote the probability of drawing the transistor of class A for the first time
	// use A2 to denote the probability of drawing the transistor of calss A for the second time
	//用A1、A2别代表第一次抽到甲类和第二次抽到甲类的概率
	int A1,A1A2;
	A1 = Combination(4,1) * Combination(5,1);
	A1A2 = Combination(4,1) * Combination(3,1);
	// owing to the conditional probability,we can conclude that
	//由条件概率可知
	printf("The probability of drawing one from class A under the condition that we've already drawn one from the class A.\n");
	long int a[2] = {A1A2,A1};
	Abbreviation(a);
	printf("%d/%d",a[0],a[1]);
	return 0;
}

写完代码我发现，上面约分的函数还需要设一个数组来存储分子和分母，是在是有点不合理
于是我想一开始就用指针来表示分子分母得了，再传它们的地址给约分函数，并在约分函数中用指针来接收，这样就方便多了。

2. 验收100件产品的方案如下：从中任取3件进行独立地测试，如果至少有一件被断定为次品，则拒绝接收该批产品。设一件次品经测试后被断定为次品的概率为0.95，一件正品经测试后被断定为正品的概率为0.99，并已知这100件产品中恰有4件次品，求该批产品能被接收的概率。

分析：首先由题目可以知道，任取三件产品，选取的正品有那么一丢丢可能是次品，而选取的次品也可能是正品，那么在选取三件产品时正品次品的判断不在于选取，而在于选取后的测试。而它们的测试又是独立的，所以它们的结果互不干扰。

我们可以将选取的三件产品的情况进行样本空间划分，然后每种情况是测试通过被接收的前提。那么最后就用全概率公式即可。

#include <stdio.h>
long int Combination(long int n,long int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}	
	return sum/p;
}

int main()
{
	// use A to denote the total probability
	//用A代表产品被接收的概率
	double A = 0;
	// use m to denote the number of quality goods
	// 用m代表正品的个数
	long int m = 0;
	while(m <= 3)
	{
		// four cycles represent four conditions
		// 4次循环代表4次情况
		double a = (Combination(96,m) * Combination(4,3 - m)) * 1.0 / Combination(100,3);
		// test the goods
		//开始测试
		int i = m;
		int j = 3 - m;
		while(i > 0)
		{
			a *= 0.99;
			i--; 
		}
		while(j > 0)
		{
			a *= 0.05;
			j--;
		}
		A += a;
		m++;
		printf("%.20f\n",a);
	}
	printf("The probability of A is :%.4f.",A);
	return 0;
}

运行结果如下：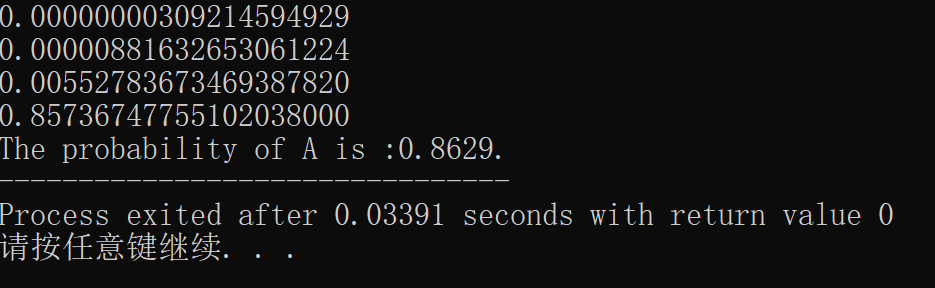

3. 若干人独立地向一游动目标射击，每人击中目标的概率都是0.6，问至少需要多少人，才能以0.99以上的概率击中目标？

分析：注意仔细理解题目，它的意思是n个人中只要有一个人击中即可。例如有甲乙两个人射击，求它们击中目标的概率就是，甲击中的概率加乙击中的概率加它们同时击中的概率。两个人以上求概率也是这样求。同时也可以由公式来表示$P(甲\cup 乙)=P(甲)+P(乙)-P(甲乙)=P(甲)+P(乙)-P(甲)P(乙)$。

但是，这样做用不光计算量很大，用C语言也很难实现啊
不过，换位思考一下，题目要求的是n个人中至少有一个击中目标，那么它的对立事件就是都没击中。
然后再用1减去对立事件的概率即可！请看👇：

#include <stdio.h>
int main()
{
	// the probability we need
	float A = 0;
	// the probability of people failing to shoot the goal
	float no = 1.0;
	// the number of people
	int n = 0;
	// the conditon
	while(A < 0.99)
	{
		no *= 0.4;
		A = 1 - no;
		n++;
	}
	printf("the number of person we need is :%d.",n);
	return 0;
}

4. 甲、乙、丙三人独立地向同一目标各射击一次，他们击中目标的概率分别为0.7，0.8和0.9，求目标被击中的概率。

分析：同样，这个题的思路跟上面的一样，但这次已经规定了人数，所以我们可以用C语言试试直接求击中的概率。

#include <stdio.h>
int main()
{
	// use a,b,c to denote the probability of 甲、乙、丙 hitting the goal
	float a = 0.7,b = 0.8,c = 0.9;
	// use 1 to denote hitting the goal
	// use 0 to denote failing to hit the goal
	// the total probability
	float A = 0;
	// use pos to denote the number of 1
	int pos = 0;
	float sum = 1.0;
	
	// the conditions of a
	for(int i = 0 ; i < 2 ; i++)
	{
		if(i == 0)
			sum *= 1 - a;
		else
		{
			pos++;
			sum *= a;
		}
		// the conditions of b
		for(int j = 0 ; j < 2 ; j++)
		{
			if(j == 0)
				sum *= 1 - b;
			else
			{
				pos++;
				sum *= b;
			}
			// the conditions of c
			for(int k = 0 ; k < 2 ; k++)
			{
				if(k == 0)
					sum *= 1 - c;
				else
				{
					pos++;
					sum *= c;
				}
				
				if(pos > 0)
					A += sum;
				// after every cycle finished,we need to divide the variable in this cycle
				// the same as below
				sum /= (k == 0 ? (1 - c) : c);
			}
			sum /= (j == 0 ? (1 - b) : b);
			pos--;
		}
		sum /= (i == 0 ? (1 - a) : a);
		pos--;
	}
	printf("The probability of incident A is : %f",A);
	return 0;
}

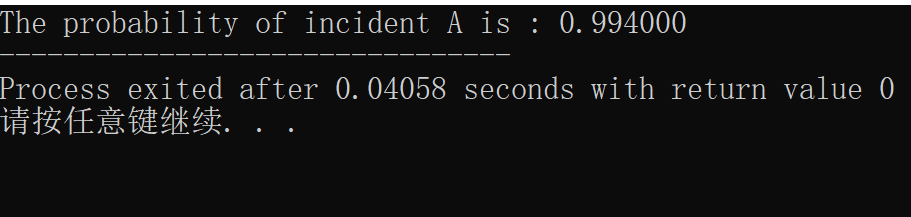
5. 8支步枪中有5支已校准过。一名射手用校准过的枪射击时，中靶的概率为0.8；用未校准过的枪射击时，中靶的概率为0.3。现从8支枪中任取一支用于射击，结果中靶。求所用的枪是校准过的概率。

分析：一般来说我们是求的中靶（事件A）的概率，但事件A的结果已经告诉你了，而我们要求的在中靶的前提下，枪是校准过的概率，如果用$B_1$表示使用校准过的枪中靶，$B_2$表示使用未校准过的枪中靶，那么我们要求的则是$P(B_1|A)$。

又因为$B_1,B_2$是样本空间的一个划分，所以我想到了全概率公式，再由已知结果，反过来求条件，则是贝叶斯公式。那么有$P(B_1|A)=\frac{P(B_1)P(A|B_1)}{P(B_1)P(A|B_1)+P(B_2)P(A|B_2)}=\frac{P(B_{1}A)}{P(A)}$
其中：
$P(B_1)=\frac{5}{8}$
$P(B_2)=\frac{3}{8}$
$P(A|B_1)=0.8$
$P(A|B_2)=0.3$
则$P(B_1|A)=\frac{40}{49}$

因为这个题我感觉C语言实现起来没啥意义，因为在C语言中也相当于是上述步骤的一个简单计算。（也可能是我还没学到家）

6. 在四次独立试验中，事件A至少发生一次的概率未0.5904，求在三次独立试验中，事件A发生一次的概率。

分析：这个题呢跟上面那个很相似，也是知道结果，不知道A试验一次发生的概率。那么首先我们需要找到A试验一次发生的概率。但由于是4次试验，如果去找它发生的概率的话计算量就有点大，不如去找它的对立事件，也就是A一次都不发生的概率。然后再求在三次独立试验中事件A发生一次的概率。

#include <stdio.h>
#include <math.h>
int main()
{
	// a denotes the probability of that A will happen at least once in four tests
	// a_ denotes the opposite incident of a
	float a = 0.5904;
	float a_ = 1 - a;
	// A denotes the probability that A will happen in one test
	float A = 1 - sqrt(sqrt(a_));
	printf("The probability of A is : %.1f\n",A);
	// then calculate the probability of that A only happens once in three tests
	// 0 denotes A do not happen
	// 1 denotes A happens
	// pos denotes the number of that A happens
	int pos = 0;
	// pro denotes the probability of one condition 
	float pro = 1;
	// tt denotes the final probability
	float tt;
	for(int i = 0 ; i < 2 ; i++)
	{
		if(i == 0)
			pro *= 1 - A;
		else
		{
			pos++;
			pro *= A;
		}
		for(int j = 0 ; j < 2 ; j++)
		{
			if(j == 0)
				pro *= 1 - A;
			else
			{
				pos++;
				pro *= A;
			}
			for(int k = 0 ; k < 2 ; k++)
			{
				if(k == 0)
					pro *= 1 - A;
				else
				{
					pos++;
					pro *= A;
				}
				if(pos == 1)
					tt += pro;
				pro /= (k == 0 ? 1 - A : A);
			}
			pro /= (j == 0 ? 1 - A : A);
			pos--;
		}
		pro /= (i == 0 ? 1 - A : A);
		pos--;
	}
	printf("The probability of incident tt is :%.3f",tt);
	return 0;
}

差不多了，好累~

最后说明一下❗️：用C语言实现不是拿到题就直接用C语言去做题，而是先在纸上完成，有个思路有个过程，用C语言实现只是去实现我们在纸上做题的这个过程，这个过程又可以用不同的方法来实现。

好了，这一次的学习就到这里，也希望能对大家有所帮助~下次再见。