支持向量机--处理非线性模型

支持向量机–处理非线性模型

如果样本集不是线性可分的，那么我们就不能像上面的处理方式一样求出$w$和$b$。

1.最小化：
$$\{\begin{array}{c}min\frac{1}{2}{\Vert W\Vert }^2+C{\sum }_{i=1}^N{\sigma }_i\cdots (1)\\ s.t.y_i[W^{\top }{\mathbf{X}}_{\mathbf{i}}+b]\ge 1-{\sigma }_i\\ {\sigma }_i\ge 0\end{array}$$
其中，${\sigma }_i$为松弛变量（Slack variable），C为事先设定的参数，i=1~N。此时，$y_i$和$x_i$是已知的，$W$,$b$,${\sigma }_i$是未知的。

2.高维映射$\phi (x)$
$$\underset{低维}{X}\stackrel{\phi }{\to }\underset{高维}{\phi (X)}$$
例：

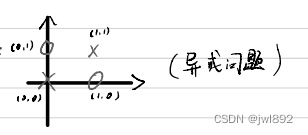
在上图坐标轴中，存在四个点，这四个点分为两类，我们怎么做才能把他们分开呢？
$$\begin{gathered} X_1=\left[\begin{array}{c}0\\ 0\end{array}\right]\in C_1{X}_2=\left[\begin{array}{c}1\\ 1\end{array}\right]\in C_1 \\ {X}_3=\left[\begin{array}{c}1\\ 0\end{array}\right]\in C_2{X}_4=\left[\begin{array}{c}0\\ 1\end{array}\right]\in C_2 \end{gathered}$$
下面我们令一种映射方式，至于为什么要这么设置，咱后面谈论
$$\phi (x):X=\left[\begin{array}{c}a\\ b\end{array}\right]\stackrel{\phi }{\to }\phi (X)=\left[\begin{array}{c}{a}^2\\ b^2\\ a\\ b\\ ab\end{array}\right]$$
由此得到：
$$\begin{gathered} \phi (X_1)=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\end{array}\right]\in C_1\phi (X_2)=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\end{array}\right]\in C_1 \\ \phi (X_3)=\left[\begin{array}{c}1\\ 0\\ 1\\ 0\\ 0\end{array}\right]\in C_2\phi (X_4)=\left[\begin{array}{c}0\\ 1\\ 0\\ 1\\ 0\end{array}\right]\in C_2 \end{gathered}$$
规定
$$W=\left[\begin{array}{c}-1\\ -1\\ -1\\ -1\\ 6\end{array}\right],b=1$$
此时
$$\begin{gathered} W^{\top }\phi (X_1)+b=1 \\ {W}^{\top }\phi (X_2)+b=3 \\ {W}^{\top }\phi (X_3)+b=1 \\ {W}^{\top }\phi (X_4)+b=-1 \end{gathered}$$
$\phi$的选择是无限维

---

(1) 我们可以不知道无限维映射$\phi (X)$的显示表达，我们只要知道，一个核函数(Kernel Function)
$$K(X_1,X_2)=\phi (X_1{)}^{\top }\phi (X_2)$$
则(1)这个优化式仍然可解。

核函数(部分)：

①高斯核
$$K(X_1,X_2)=e^{-\frac{{\Vert X_1-X_2\Vert }^2}{2{\sigma }^2}}$$

$$=\phi (X_1{)}^{\top }\phi (X_2)$$

②
$$K(X_1,X_2)=({X_1}^{\top }{X}_2+1{)}^d$$

$$=\phi (X_1{)}^{\top }\phi (X_2)$$

(2) $K(X_1,X_2)$能写成$\phi (X_1{)}^{\top }\phi (X_2)$的充要条件(Mercer’s Theorem)：

①$K(X_1,X_2)=K(X_2,X_1)$；

②对任意$C_i(常数),{\mathbf{X}}_{\mathbf{i}}(向量)$，$(i=1\sim N)$，有(半正定性)：
$$\sum _{i=1}^N\sum _{j=1}^N{C}_i{C}_{j}K({\mathbf{X}}_{\mathbf{i}},{\mathbf{X}}_{\mathbf{j}})\ge 0$$

---

**优化问题：**训练样本集 { ( X i , y i ) } i = 1 ∼ N \left \{ (\boldsymbol{X_i},y_i) \right \} _{i=1 \sim N} {(Xi​,yi​)}i=1∼N​

(其中${\mathbf{X}}_{\mathbf{i}}$为向量，$y_i$为标签)
$$\{\begin{array}{c}min\frac{1}{2}{\Vert W\Vert }^2+C{\sum }_{i=1}^N{\sigma }_i\\ s.t.y_i[W^{\top }\phi (X_i)+b]\ge 1-{\sigma }_i\\ K(X_1,X_2)=\phi (X_1{)}^{\top }\phi (X_2)\end{array}$$

---

在此之前，简单说一下优化理论–原问题和对偶问题。

(1)原问题(Prime Problem)
$$\begin{gathered} minf(w) \\ s.t{g}_i(w)\le 0(i=1\sim k) \\ s.t{h}_i(w)=0(i=1\sim m) \end{gathered}$$
(2)对偶问题(Dual Problem)

①定义
$$\begin{gathered} L(w,\alpha ,\beta ) \\ =f(w)+\sum _{i=1}^k{\alpha }_i{g}_i(w)+\sum _{i=1}^m{\beta }_i{h}_i(w) \\ =f(w)+{\alpha }^{\top }g(w)+{\beta }^{\top }h(w) \end{gathered}$$
②对偶问题定义
m a x Θ ( α , β ) = i n f { L ( w , α , β ) } s . t α i ≥ 0 ( i = 1 ∼ k ) max\Theta (\alpha,\beta)=inf\left \{ L(w,\alpha,\beta) \right \}\\ s.t \qquad \alpha_i \ge 0 \qquad (i=1 \sim k) maxΘ(α,β)=inf{L(w,α,β)}s.tαi​≥0(i=1∼k)
(其中$inf$为求所有$w$的最小值)

定理：

如果$w^{\ast }$是原问题的解，而${\alpha }^{\ast },{\beta }^{\ast }$是对偶问题的解，则有：
$$f(w^{\ast })\ge \Theta ({\alpha }^{\ast },{\beta }^{\ast })$$
证：
Θ ( α ∗ , β ∗ ) = i n f { L ( w , α ∗ , β ∗ ) } ≤ L ( w ∗ , α ∗ , β ∗ ) = f ( w ∗ ) + ∑ i = 1 k α i ∗ g i ( w ∗ ) + ∑ i = 1 m β i ∗ h i ( w ∗ ) ≤ f ( w ∗ ) \Theta (\alpha^*,\beta^*)=inf\left \{ L(w,\alpha^*,\beta^*) \right\}\\ \le L(w^*,\alpha^*,\beta^*) =f(w^*)+\sum_{i=1}^k\alpha_i^*g_i(w^*)+\sum_{i=1}^m\beta_i^*h_i(w^*)\\ \le f(w^*) Θ(α∗,β∗)=inf{L(w,α∗,β∗)}≤L(w∗,α∗,β∗)=f(w∗)+i=1∑k​αi∗​gi​(w∗)+i=1∑m​βi∗​hi​(w∗)≤f(w∗)

$$(其中{\alpha }_i^{\ast }\ge 0,g_i(w^{\ast })\le 0,h_i(w^{\ast })=0)，证毕$$

定义：
$$G=F(w^{\ast })-\Theta ({\alpha }^{\ast },{\beta }^{\ast })\ge 0$$
$G$叫做原问题与对偶问题的间距(Duality Gap)。（对于某些特定的优化问题，可以证明对偶间距$G=0$。)

强对偶问题：

​ 若$f(w)$为凸函数，且$g(w)=Aw+b,h(w)=Cw+d$，则此优化问题的原问题与对偶问题间距为0，即$f(w^{\ast })=\Theta ({\alpha }^{\ast },{\beta }^{\ast })$，
$$对\forall i=1\sim k,\underset{KKT条件}{\underbrace{{\alpha }_i^{\ast }=0,或g_i(w^{\ast })=0}}$$

---

接下来，试着把上述优化问题转化为对偶问题，以便求解

OK，现在把上面说的原对偶问题总结一下：

①原问题：
$$\begin{gathered} minf(w) \\ s.t{g}_i(w)\le 0(i=1\sim k) \\ s.t{h}_i(w)=0(i=1\sim m) \end{gathered}$$
②对偶问题：
$$L(w,\alpha ,\beta )=f(w)+\sum _{i=1}^k{\alpha }_i{g}_i(w)+\sum _{i=1}^m{\beta }_i{h}_i(w)$$

m a x Θ ( α , β ) = i n f { L ( w , α , β ) } s . t α i ≥ 0 ( i = 1 ∼ k ) max\Theta (\alpha,\beta)=inf\left \{ L(w,\alpha,\beta) \right \}\\ s.t \qquad \alpha_i \ge 0 \qquad (i=1 \sim k) maxΘ(α,β)=inf{L(w,α,β)}s.tαi​≥0(i=1∼k)

③KKT条件：
$$\forall i=1\sim k,有{\alpha }_i^{\ast }=0,或g_i(w^{\ast })=0$$

SVM是这样的：
$$min\frac{1}{2}{\Vert W\Vert }^2+C\sum _{i=1}^N{\sigma }_i(凸函数)\Rightarrow 对应原函数的f(w)$$

$$s.t\{\begin{array}{c}{y}_i[W^{\top }\phi (X_i)+b]\ge 1-{\sigma }_i\\ {\sigma }_i\ge 0(i=1\sim k)\end{array}$$

但是为了对应原问题，我们对他做一些改变：
$$min\frac{1}{2}{\Vert W\Vert }^2-C\sum _{i=1}^N{\sigma }_i$$

$$s.t\{\begin{array}{c}1+{\sigma }_i-y_i{W}^{\top }\phi (X_i)-y_{i}b\le 0\\ {\sigma }_i\le 0(i=1\sim k)\end{array}$$

对偶问题：
$$max\Theta (\alpha ,\beta )=\underset{所有(W,{\sigma }_i,b)}{\inf }\left\{\frac{1}{2}{\Vert W\Vert }^2-C\sum _{i=1}^N{\beta }_i{\sigma }_i+\sum _{i=1}^N{\alpha }_i\left[1+{\sigma }_i-y_i{W}^{\top }\phi (X_i)-y_{i}b\right]\right\}$$

$$s.t\{\begin{array}{c}{\alpha }_i\ge 0\\ {\beta }_i\ge 0\end{array}$$

令上面问题中大括号内的内容为$L(w,\sigma ,b)$
$$\frac{\partial L}{\partial W}=0\Rightarrow W=\sum _{i=1}^N{\alpha }_i{y}_i\phi (X_i)$$

$$\frac{\partial L}{\partial {\sigma }_i}=0\Rightarrow {\beta }_i+{\alpha }_i=C$$

$$\frac{\partial L}{\partial b}=0\Rightarrow \sum _{i=1}^N{\alpha }_i{y}_i=0$$

把上面得到的结果带入到对偶问题式子里，得
$$\begin{gathered} max\Theta (\alpha ,\beta )=\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(X_i,X_j) \\ s.t\{\begin{array}{c}0\le {\alpha }_i\le c\\ {\sum }_{i=1}^N{\alpha }_i{y}_i=0\end{array} \end{gathered}$$
下面是上面求导中的某两步，仅供参考：
$$\begin{gathered} \frac{1}{2}{\Vert W\Vert }^2=\frac{1}{2}{W}^{\top }W \\ =\frac{1}{2}{\left\{\sum _{i=1}^N{\alpha }_i{y}_i\phi (X_i)\right\}}^{\top }\left\{\sum _{j=1}^N{\alpha }_j{y}_j\phi (X_j)\right\} \\ =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\phi (X_i{)}^{\top }\phi (X_j) \\ =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(X_i,X_j) \end{gathered}$$

$$\begin{gathered} -\sum _{i=1}^N{\alpha }_i{y}_i{W}^{\top }\phi (X_i) \\ =-\sum _{i=1}^N{\alpha }_i{y}_i{\left\{\sum _{j=1}^N{\alpha }_j{y}_j\phi (X_j)\right\}}^{\top }\phi (X_i) \\ =-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\phi (X_j{)}^{\top }\phi (X_i) \\ =-\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(X_i,X_j) \end{gathered}$$

接下来要求b，要用到KKT条件：

对任意的$i=1\sim N$,

①要么${\beta }_i=0$，要么${\sigma }_i=0$；

②要么${\alpha }_i=0$，要么$1+{\sigma }_i-y_i{W}^{\top }\phi (X_i)-y_{i}b=0$。

取一个${\alpha }_i$，满足$0<{\alpha }_i<c$，$⟹{\beta }_i=c-{\alpha }_i>0,此时\{\begin{array}{c}{\beta }_i\ne 0\Rightarrow {\sigma }_i=0\\ {\alpha }_i\ne 0\Rightarrow 1+{\sigma }_i-y_i{W}^{\top }\phi (X_i)-y_{i}b=0\end{array}$,
$$\Rightarrow b=\frac{1-y_i{W}^{\top }\phi (X_i)}{y_i}=\frac{1-y_i{\sum }_{j=1}^N{\alpha }_j{y}_{j}K(X_i,X_j)}{y_i}$$

SVM算法：

①训练流程：

输入 { ( X i , y i ) } i = 1 ∼ N \left \{ (X_i,y_i) \right \} _{i=1\sim N} {(Xi​,yi​)}i=1∼N​

（解优化问题）

最大化：$\Theta (\alpha )={\sum }_{i=1}^N{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(X_i,X_j)$

限制条件：$\{\begin{array}{c}0\le {\alpha }_i\le c\\ {\sum }_{i=1}^N{\alpha }_i{y}_i=0\end{array}$

算b，找一个$0<{\alpha }_i<c$,$b=\frac{1-y_i{\sum }_{j=1}^N{\alpha }_j{y}_{j}K(X_i,X_j)}{y_i}$

②测试流程：

测试样本X

​ 若${\sum }_{i=1}^N{\alpha }_i{y}_{i}K(X_i,X)+b\ge 0，则y=+1$

​ 若${\sum }_{i=1}^N{\alpha }_i{y}_{i}K(X_i,X)+b<0，则y=-1$。

限制条件：$\{\begin{array}{c}0\le {\alpha }_i\le c\\ {\sum }_{i=1}^N{\alpha }_i{y}_i=0\end{array}$

算b，找一个$0<{\alpha }_i<c$,$b=\frac{1-y_i{\sum }_{j=1}^N{\alpha }_j{y}_{j}K(X_i,X_j)}{y_i}$

②测试流程：

测试样本X

​ 若${\sum }_{i=1}^N{\alpha }_i{y}_{i}K(X_i,X)+b\ge 0，则y=+1$

​ 若${\sum }_{i=1}^N{\alpha }_i{y}_{i}K(X_i,X)+b<0，则y=-1$。