容斥原理+简单博弈论（找个时间补充一下sg，希望我记得）

---

容斥原理

解析容斥原理

先说一下容斥原理：
在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。
容斥原理的公式：

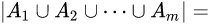
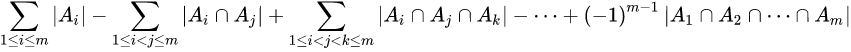
提到容斥原理肯定少不了韦恩图

如图2，4，6是任意两个圆的公共面积，5是三个圆的公共面积，设三个圆为A，B，C
那么三个圆构成的面积
=S_A+S_B+S_C-S_A+B-S_A+C-S_B+C+S_A+B+C
解释一下：起先三个完整的圆面积相加，因为任意两个圆之间都有公共面积，也就是说任意两个圆的公共面积被加了两次，那么就把这三块两个圆的公共面积各减一份，也就是S_A+S_B+S_C-S_A+B-S_A+C-S_B+C，但减去的三个面积都包含那一块三个圆叠加的面积，这一块面积在S_A+S_B+S_C出现了三次，在-S_A+B-S_A+C-S_B+C出现了三次，所以这一块面积就没算上，所以最终结果是S_总=S_A+S_B+S_C-S_A+B-S_A+C-S_B+C+S_A+B+C

同理，对于四个圆组成的图形求总面积
首先分别加上四个圆的面积
然后减去两个圆相交集合的面积，因为在进行四个圆面积相加的时候每一块两个圆的交集都出现了两次C（2，1）
再加上三个圆相交的面积，因为每个三个圆交集的面积都在减去两个圆交集的面积的时候被减去三次C（3，2），但是在分别加上四个圆面积时候每个三个圆集合都被加上了三次C（3，1），前两次加减抵消就得再加上
再减去四个圆相交的面积，四个圆的集合在第一次操作出现了四次C（4，1），第二次操作出现了六次C（4，2），第三次操作出现了四次C（4，3），所以4-6+4-1=1，所以第四步操作再对四个圆集合这部分再减一次C（4，4）。
可以发现：在对i个圆的交集进行处理时，n个圆的交集出现的次数是C（n，i），理解就是n个圆中任选i个圆作为i个圆交集的面积的构造者。

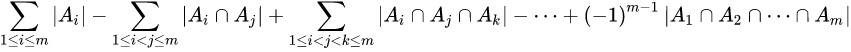
那么对于i个圆交集的面积在式子中为什么奇数个圆集合的面积前是加偶数个是减就可以证明了
C（i，1）-C（i，2）+C（i，3）…+(-1)^n-1C（i，i）=1；，满足i个集合的面积只出现一次。

(1-x)ⁿ=C(n,0)x⁰-C(n,1)¹x¹+C(n,2)x²…+(-1)ⁿ*C(n,n)xⁿ
把x=1代入也就是C(n,0)-C(n,1)+C(n,2) … +(-1)ⁿ*C(n,n)=0
所以C（i，1）-C（i，2）+C（i，3）…+(-1)^n-1C（i，i）=1。

任意k个圆的交集在式子中的结果是 (-1)^cnt-1 * n / t(cnt的参与的质数个数，t是因子）

芜湖~还好高中学的排列组合还没忘光。

题目

题目链接–能被整除的数

这道题其实就是先判断哪些因子相乘能比n小，那么这些相乘的结果都可以在1–n中找到倍数，那么怎么解决这些因子相乘的搭配问题，下面这种写法我感觉真的很好
for (int i = 1; i < 1 << m; i++) (1<<m=pow(2,m))
for (int j = 0; j < m; j++)

通过数的二进制来表示因子的搭配，因为二进制的每位只有1或者0，可以用来表示当前因子是否参与搭配
比如2=10，第0位为0，第1位为1就表示该因数搭配只有prime[1]
如果是3=11，第0位为1，第1位为1就表示该因数搭配只有prime[0]*prime[1]

在运算过程中记得判断该因子搭配的结果是否比n大，如果比n大就没有存在的可能

#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
int prime[20];
int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 0; i < m; i++)
		cin >> prime[i];
	int cnt = 0;
	ll res = 0, t;
	for (int i = 1; i < 1 << m; i++) {//列举搭配可能性
		cnt = 0, t = 1;
		for (int j = 0; j < m; j++) {
			if (i >> j & 1) {
				if (prime[j] * t > n) {
					t = -1;
					break;
				}
				t *= prime[j];//记录搭配后的因子
				cnt++;//记录参与因子搭配中质数的个数
			}
		}
		if (t == -1) continue;
		res += pow(-1, cnt - 1) * (int)(n / t);
	}
	cout << res;
	return 0;
}

简单博弈论

经典–Nim游戏

通常的Nim游戏的定义是这样的：有若干堆石子，每堆石子的数量都是有限的，合法的移动是“选择一堆石子并拿走若干颗（不能不拿）”，如果轮到某个人时所有的石子堆都已经被拿空了，则判负（因为他此刻没有任何合法的移动），假设两个人都绝顶聪明。

对于Nim游戏的玩家只有两种游戏结局，必败和必胜。

一般来说我们只对先手的游戏结局进行分析，这里有一个结论，假设有n堆石子，石子个数分别为a1,a2,a3…，如果满足a1^ a2^ a3^ …^ an=0 ,则先手必败，如果a1^ a2^ a3^… ^an!=0，则先手必胜。

接下来对这个结论进行一下证明：

证明先手必胜情况
首先因为0 ^ 0 ^ 0 ^ …^ 0=0得出需要对下面的式子进行证明（只有让式子最后变成0 ^ 0 ^ 0 ^ …^0=0才能实现胜利）

• 先证明a1 ^ a2 ^ a3 ^ … ^ an!=0，则先手必胜：
• （能确保是由先手实现0 ^ 0 ^ 0 ^ …^0=0，导致后手不能再进行操作）： 设a1^ a2^ a3^… ^an=x，x的第一位为1的数是第k位，那么一定存在ai第k位为1，那么ai
  ^x<ai(0与任何数异或，原数不变（二进制），所以ai第k位数之前的不变，异或之后第k位数变为0->ai
  ^x<ai），所以每次对第i堆（ai）取ai-ai ^x（ai-ai ^x>0,满足）个石子 ，ai-（ai-ai ^x)=ai
  ^x,所以取完石子式子变成了a1 ^ a2 ^a3 ^… ai ^x… ^an=x
  ^x=0，一直按这个方法取石子就可以使得后手局面一直处于必败状态直到所有石子被取完，所以先手胜。
• 再证明a1^ a2^ a3^ …^ an=0 ,则先手必败：
  那就证明无论怎么拿石子a1 ^ a2^ a3^ …^ Ai ^ … ^ an！=0， 我们用反证法证明，假设对ai取玩石子后ai变成Ai，如果可以是0，则a1^ a2^ a3^ …^ Ai ^ … ^ an=0 ,且a1 ^ a2^ a3^ …^ ai^… ^ an=0,两式子异或，则ai ^Ai=0,那么ai=Ai，就是一个石子都不拿，与题意矛盾（不能不拿石子）

游戏操作就是：当初始条件满足a1 ^ a2 ^ a3 ^ … ^ an!=0，先手操作，使得操作结果是a1 ^ a2 ^ a3 ^ … ^ an=0，也就是到后手的情况一定是0，这样无论后后手如何操作，先手都有办法让抛到后手手里的结果是a1 ^ a2 ^ a3 ^ … ^ an=0，那么最终0^ 0^ 0^… ^0=0一定是抛到后手手里的，所以先手胜。
如果开始a1 ^ a2 ^ a3 ^ … ^ an==0，那么无论如何操作抛到后手的都是a1 ^ a2 ^ a3 ^ … ^ an!=0局面，后手永远不可能数，所以只有先手会输，所以后手胜。

题目链接–简单Nim游戏

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int n;
    cin>>n;
    int res=0,k;//0^k=k;
    for(int i=0;i<n;i++)
    {
        cin>>k;
        res^=k;
    }
    if(res==0) cout<<"No";
    else cout<<"Yes";
    return 0;
}

集合–Nim游戏

这是一个有向图游戏，当前局面经过一定操作会变成新的局面，然后对于新的局面继续重复之前的操作，直至对新局面无法再进行操作。

Mex是找到不属于集合的最小自然数

对于sg函数，定义sg（终点）=0，如何求每一个状态x的sg（x）：看一下x这个局面通过我们的操作可以变成哪些局面y1，y2…yk，sg（x）=Mex{sg（y1），sg（y2）…sg（yk）}，sg（x）就是不属于它操作后的sg的集合的最小自然数

for (int i = 0;; i++) 
		if (!count(V.begin(), V.end(), i)) 
			return h[x] = i;

举个例子
终点有3和5（出度为0），4节点只指向5，所以sg（4）=1，2节点指向3和4，sg（3）=0，sg（4）=1，所以sg（2）=2，7节点只指向节点6，sg（6）=1，所以除了1以外的最小自然数是0，所以sg（7）=0.

这个只有一个有向图，那么这个有向图sg（起点）为0就是必败，sg（起点）不为0就是必败
为什么呢，简单证明一下：
终点状态是0。任意一个非0都可以只通过一步走到0，为啥？因为现状态是操作后状态集合外的最小自然数，既然现状态非0，那么操作后的状态就一定有0，和之前简单的nim游戏一样，只要先手当前状态不为0，那么下一步就一定可以让对手处在状态为0，经过若干次操作下一步对手都处于0位置，最终对手处于终点位置，对手无法再进行操作了，先手胜。处于0状态的选手没法到0，就是如果当前状态为0，下一步一定不能到终点。
如果是多个无向图，选手每次选择一个图进行操作，直到所有图都不能操作，那么就是sg(x₁)^sg(x~2~)… ^{sg(x~k~)=0，先手必败，sg(x~1~)}sg(x₂)^… ^sg(x_k)!=0先手必胜

证明类似简单nim游戏

• 每个局面都不能走，那么sg(x_i)=0,0^ 0^ …^0=0,必败状态
• 如果当前所有状态异或值不是0，设sg(x₁)^sg(x~2~)… ^sg(x_k)=x != 0,那么一定可以找到一个局面sg(x_i)^x<sg(x_i) ----(x第k位为1，那么sg(x_i)第k为一定是1），所以通过sg(x)变成sg(x_i)^{x一定是成立的，那么sg(x~1~)}sg(x₂)^… ^sg(x~k~) x=x^{x=0,也就是只有从sg(x~i~)走到sg(x~i~)}x就可以使局面变成0，使对手处于必败，此时先手胜。
• sg(x₁)^sg(x~2~)… ^{sg(x~k~)=0，怎么变sg(x~1~)}sg(x₂)^… ^sg(x~k~)都不会为0
  反证：假装将sg(x_i)变成Sg(x_i)后仍然为0，那么sg(x₁)^sg(x~2~)… ^Sg(i) ^… ^sg(x_k)=0, sg(x₁)^sg(x~2~)… ^sg(i) ^… ^sg(x_k)=0,两个式子异或，所以Sg(i) ^sg(i)=0, Sg(i)=sg(i)矛盾。

思路听听懂了，代码一写傻眼了…主要sg函数咋实现之前从来没接触过呜呜我好菜
上代码：
题目链接–集合-Nim游戏

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 105, M = 10005;
int n, k, s[N], h[M];
int sg(int x) {
	if (h[x] != -1) return h[x];//分配情况已经存在了，不用再次进行记忆化搜索
	vector<int>V;

	for (int i = 0; i < k; i++) {
		int t = s[i];
		if (x - t >= 0) V.push_back(sg(x - t));
	}
	
	for (int i = 0;; i++) {
		if (!count(V.begin(), V.end(), i)) 
			return h[x] = i;//找出不属于分配情况集合的最小自然数
	}
}
int main()
{
	cin >> k;
	for (int i = 0; i < k; i++)
		cin >> s[i];

	cin >> n;
	memset(h, -1, sizeof h);
	//用来判断这个树的分配情况是否已经存在了，减少时间复杂度
	int res = 0, x;
	for (int i = 0; i < n; i++) {
		cin >> x;
		res ^= sg(x);
	}
	if (!res) cout << "No" << endl;
	else cout << "Yes" << endl;
	return 0;
}

台阶–Nim游戏

先分析一下台阶Nim游戏：
台阶Nim游戏只要分析奇数台阶就行，如果各奇数台阶上石子数异或结果为0先手必败SG(x₁) ^ SG(x₃)^ … ^ SG(x_2k+1)=x!=0，，各奇数台阶上石子数异或结果不为0先手必胜。

证明一下：

• 当此时所有台阶的石子都为0时，选手无法再进行操作，游戏结束，也满足终止状态奇数台阶异或和为 0。

为什么只考虑奇数台阶而不考虑偶数台阶，因为任何一方对偶数台阶的拿走x石子移动到奇数台阶，另一方都可以将该奇数台阶的x个石子再推导下一级台阶，保证奇数台阶上各台阶石子数始终不变，所以不用考虑偶数台阶。

以下按照先手必胜情况分析：

• 当所有奇数台阶上石子数异或结果不为0，先手进行一定的操作可以使当前局面变成0，那么此时到后手手中所有奇数台阶上石子数异或结果为0，反复操作一直到所有台阶上石子都0，这种状态仍然是在后手手中，后手必败。
• 先手操作完后后手有两种操作情况，一种是移动偶数台阶上的石子，将偶数台阶上的石子移动到奇数台阶上，假设移动了x个石子，那么此时偶数台阶下一个的奇数台阶就多了x个石子，此时先手再将该奇数台阶的x个石子移动到下一级偶数台阶或者地面，那么奇数台阶上各台阶石子始终不变，所有奇数台阶上石子数异或结果不变，不为0；如果后手移动的是奇数台阶上的石子，使得所有奇数台阶上石子数异或结果为0，先手一定能通过一定操作使得所有奇数台阶上石子数异或结果不为0，这块参照经典Nim游戏。

其实结论挺好证明成立的，难在这个结论是怎么推导出来的。–例举+推理+证明

一顿分析猛如虎，一看代码十四行
芜湖博弈论的分析好难，想出博弈论的到底是什么能人Orrz

题目链接–台阶-Nim游戏

#include<iostream>
using namespace std;
int main()
{
	int n, res = 0, k;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> k;
		if (i % 2) res ^= k;
	}
	if (!res) cout << "No" << endl;
	else cout << "Yes" << endl;
	return 0;
}

拆分–Nim游戏

模型：n堆石子，任意拿走一堆然后放入两堆规模更小的，两堆石子总数可以大于拿走那堆的总数，但是单堆石子总数一定小于拿走那堆石子的总数
不管堆数的变化，一堆石子的石子数一定是不断变小的，不断变小就一定会变到0，所以所有石子堆最终都可能变成0，so游戏有结束时刻。

解题思路分析
给定n堆石子，可以把每堆看成一个独立的局面，求完每堆石子的sg将他们异或起来，如果所有石子堆的sg异或结果为0那么先手必败，如果所有sg异或结果不为0先手必胜。
那么每个局面的sg如何求(重点)
就是将当前状态变化为下一状态，类似上一次的无向图/集合–Nim游戏，不断的分解，取任意情况下的当前局面Sg(x),分解成a，b，那么sg(x)=sg(x)^sg(b),后面已经是不断分解，不断重复上面求当前sg状态的操作，直至游戏结束是sg(终点)=0.

游戏终点的sg为0，如果当前局面为1，那么下一步操作一定可以到达0（终点），如果当前局面为0，无论怎么操作都不可能到达1，这一部分的证明可以仿照上面集合Nim游戏。
题目链接–拆分-Nim游戏

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 105;
int f[N];
int sg(int x) {
	if (f[x] != -1) return f[x];
	vector<int>V;
	for (int i = 0; i < x; i++)//默认第二堆石子数小于等于第一堆,i,j表示两堆石子分别的石子数
		for (int j = 0; j <= i; j++) {
			V.push_back(sg(i) ^ sg(j));//sg(i,j)=sg(i)^sg(j)  暂时先当个定理用，以后会证明了再补充
		}
	for (int i = 0;; i++)
		if (!count(V.begin(), V.end(), i)) return f[x] = i;
}
int main()
{
	int n, x, res = 0;
	cin >> n;
	memset(f, -1, sizeof f);
	for (int i = 0; i < n; i++) {
		cin >> x;
		res ^= sg(x);
	}
	if (!res) cout << "No";
	else cout << "Yes" << endl;
	return 0;
}

芜湖四种简单的博弈论游戏的模型总算整理完了