令人稀里糊涂的虚短虚断
想必好多人在学习硬件电路分析时,都会听到虚短虚断这个专业术语,但是对于新手玩家,这个术语不好理解,比如我自己,经常将这两个概念混淆。最近刷到大佬的视频,讲解的非常简洁易懂,特意做个小笔记!
1.电子小白学不会运放?一开始掌握这两个用法就够了!
2.如何理解运放的虚短虚断,他们有啥用?
运算放大电路的特点
对于如下运放结构图:
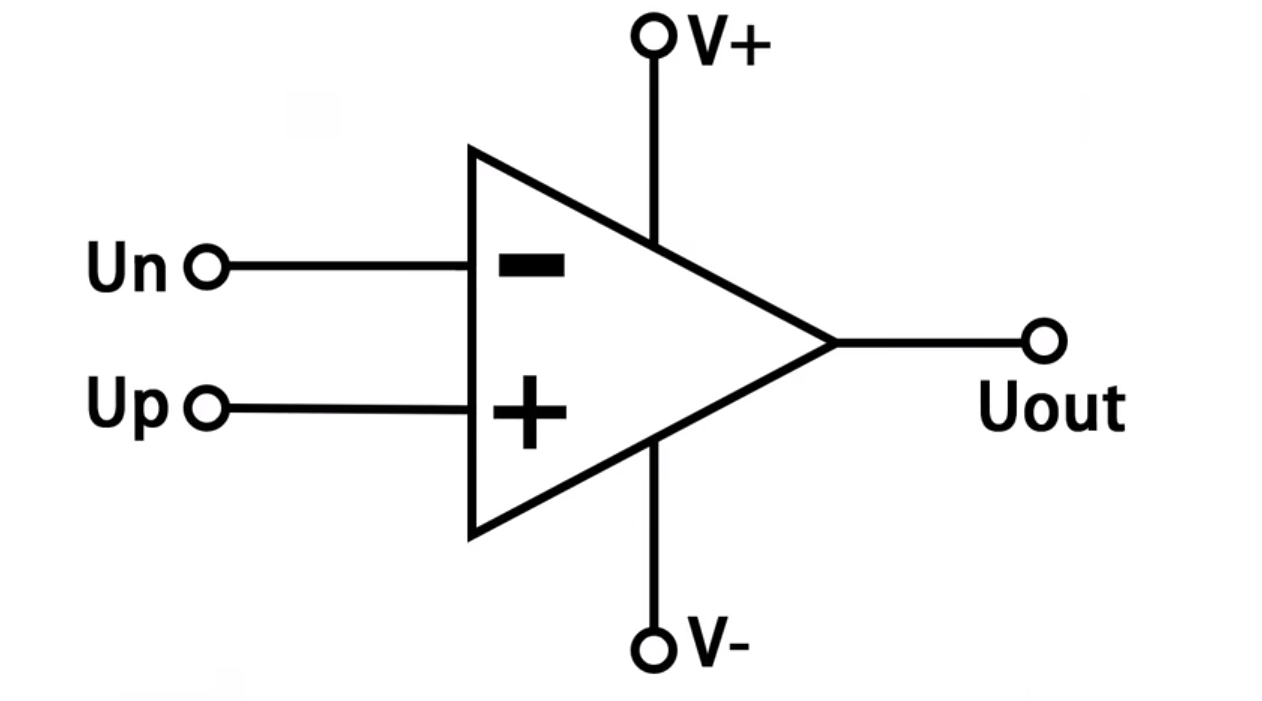
- 当 U p > U n U_{p}>U_{n} Up>Un时, U o u t = V + U_{out}=V_{+} Uout=V+
- 当 U p < U n U_{p}<U_{n} Up<Un时, U o u t = V − U_{out}=V_{-} Uout=V−
- 当 U p ≈ U n U_{p} \approx U_{n} Up≈Un时, U o u t = A ( U p − U n ) U_{out}=A(U_{p}-U_{n}) Uout=A(Up−Un)(A为放大倍数)
当引入负反馈时,如下所示:
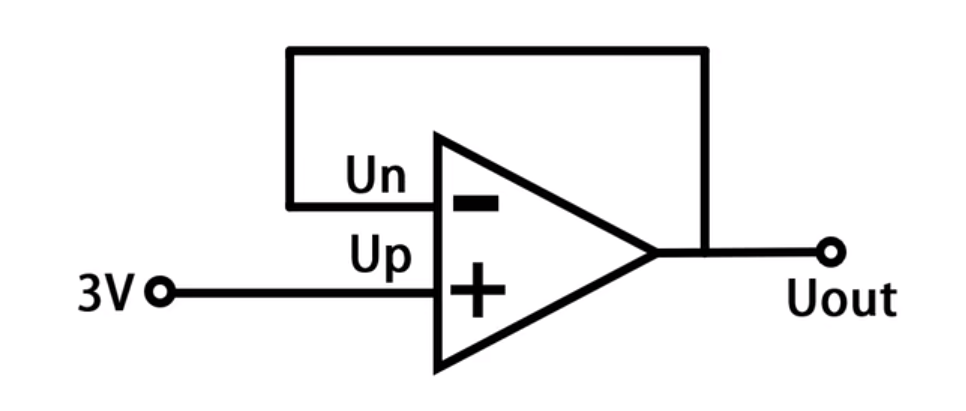
负反馈可以修正
U
n
U_{n}
Un的大小,使
U
n
U_{n}
Un无限逼近
U
p
U_{p}
Up的值,从而使运放进入线性放大区间,从而实现信号的放大
虚断----输入阻抗无穷大
如下所示:当一个信号接入到输入端,此时流过该线路中的电流为0
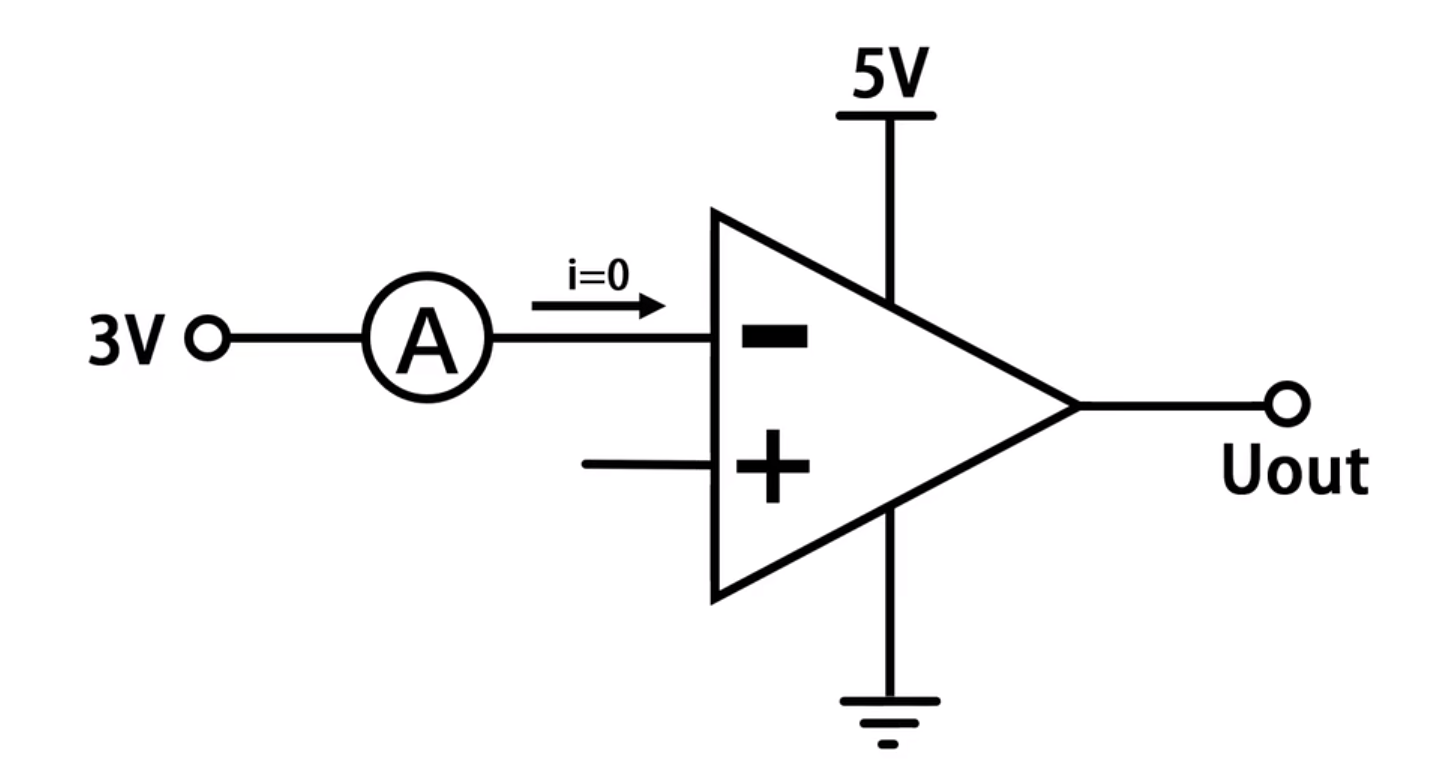
那为什么流过的电流为0呢?答案就是因为远算放大器的输入阻抗无穷大
正因为如此,流过的电流为0,如同断路的状态,故称之为“虚断”
虚短----负反馈的存在
如下所示:
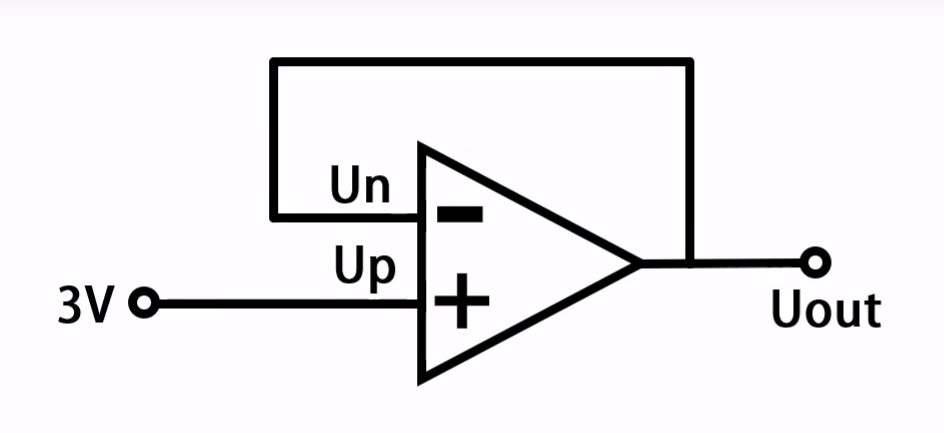
由于负反馈的存在,使 U n U_{n} Un无限逼近 U p U_{p} Up的值,从而使得 U n U_{n} Un与 U p U_{p} Up近似短路,故称之为“虚短”
电路分析步骤
对于如下的运算电路:
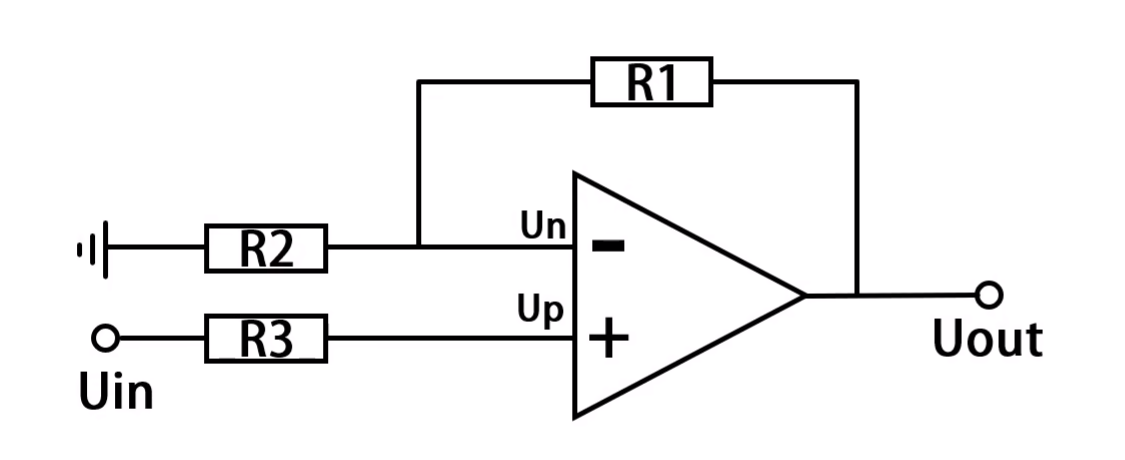
- 由于输入阻抗无穷大(即虚断),流过电阻 R 3 R_{3} R3进入正输入端的电流 I + = 0 I_{+}=0 I+=0,或记为 I 3 = 0 I_{3}=0 I3=0
- 电阻 R 3 R_{3} R3两端的电压 U 3 = I 3 × R 3 = 0 U_{3}=I_{3}\times R_{3}=0 U3=I3×R3=0
- U p = U i n − U 3 = U i n − 0 = U i n U_{p}=U_{in}-U_{3}=U_{in}-0=U_{in} Up=Uin−U3=Uin−0=Uin
- 由于负反馈的存在(即虚短),使得 U n = U p = U i n U_{n}=U_{p}=U_{in} Un=Up=Uin
- 在负反馈通路中,电流由 U o u t U_{out} Uout流向 U n U_{n} Un,故流过电阻 R 1 R_{1} R1的电流为 I 1 = U o u t − U n R 1 I_{1}=\frac{U_{out}-U_{n}}{R_{1}} I1=R1Uout−Un
- 流过电阻 R 2 R_{2} R2的电流 I 2 = U n − 0 R 2 I_{2}=\frac{U_{n}-0}{R_{2}} I2=R2Un−0
- 根据电流分流,可知 I 1 = I 2 + I − = I 2 I_{1}=I_{2}+I_{-}=I_{2} I1=I2+I−=I2(虚断,负输入端 I − = 0 I_{-}=0 I−=0)
- 所以根据 I 1 = I 2 I_{1}=I_{2} I1=I2,得出关系: U o u t = ( 1 + R 1 R 2 ) U n U_{out}=(1+\frac{R_{1}}{R_{2}})U_{n} Uout=(1+R2R1)Un
- 在第4步中有 U n = U i n U_{n}=U_{in} Un=Uin,故可得输出与输入之间的关系: U o u t = ( 1 + R 1 R 2 ) U i n U_{out}=(1+\frac{R_{1}}{R_{2}})U_{in} Uout=(1+R2R1)Uin

























 4070
4070

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










