【状态估计】【KF、DKF、SMDKF 、CI 、ICF、HCMCI】离散时间线性系统的基于共识的分布式滤波器的稳定性与最优性分析（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章下载

---

💥1 概述

摘要
本文研究了基于共识的分布式滤波器在离散时间设置中对有向图和无向图的稳定性和最优性如何取决于共识步数。通过引入两种新算法，一种基于估计的动态平均的简化版本，另一种更复杂的版本，其中还交换了本地误差协方差矩阵，我们能够得出完整的理论分析。特别是，我们表明仅通过动态平均就足以近似最优集中式估计，如果共识步数足够大，并且共识步数所需的稳定性可以通过分布式方式计算得出。这些结果揭示了在线性时不变系统的基本情况下，这类算法的所有现有提案所共享的优势以及基本限制，并且这对于分析更复杂情况具有相关性。

近年来，低成本传感器的可用性和无线网络的普及促进了基于无线传感器网络的应用的发展，这些应用涵盖了广泛的领域，如环境监测（Silva等，2015）、空中目标跟踪（Sun & Xin，2015）、空间态势感知（Jia等，2016）、航天器导航（Vu & Rahmani，2015）等。主要是由于人们对将无线传感器网络应用于大规模估计和控制问题的兴趣激增，分布式估计和滤波已成为滤波理论领域中最活跃的话题之一（He等，2020）。

分布式估计是基于多个传感器节点的合作进行大规模感知任务的使用，这些任务无法由单个设备完成。在完全分布式的架构中使用冗余和协作信息源可能增强部署的灵活性、效率、鲁棒性和估计的准确性。分布式算法规定了信息如何在网络的节点之间交换和处理，以便在每个节点只能与其邻居通信的约束下达到目标系统状态的共享估计。额外的挑战包括单个节点的有限处理能力，通常是低成本设备，有限的通信带宽，动态网络拓扑，不可靠通信信道和/或通信延迟的存在，传感器相对于其对目标系统的测量的异质性以及有限的能量（He等，2020）。通常假设节点可以是通信节点，只具有通信和处理能力，或者是传感器节点，除了具有感知能力外还具有（Battistelli等，2015）。

鉴于此，分布式估计算法评估了以下几个方面：（a）估计的准确性，线性高斯系统的最佳参考是使用所有传感器的测量值的集中式卡尔曼滤波器；（b）节点之间估计的一致性，在估计用于控制目的时尤为重要；（c）通信成本，表示相邻节点之间交换的信息量；（d）能够在最小的网络连接和系统集体可观测性要求下保证稳定性的能力。

在共识滤波器中，相邻节点之间交换的信息可以是本地状态估计（估计一致性，CE），如卡尔曼共识滤波器（KCF）（Olfati-Saber，2007），也可以是信息（矩阵-向量）对（信息一致性，CI（Battistelli等，2015）），或者创新信息对（测量一致性，CM）。 CI滤波器（Battistelli和Chisci，2014，He等，2018，Hlinka等，2014）在执行一个共识步骤时退化为协方差交集方法（Julier＆Uhlmann，2017），它们通常不会收敛到最优的集中式估计，无论共识步骤和融合策略的数量如何，因为它们未充分考虑创新项，但具有良好的稳定性属性，并且即使对于有限数量的共识迭代，也会生成无偏差和一致的局部估计。 CM滤波器包括最初在Olfati-Saber（2005）中提出的CM卡尔曼滤波器（CMKF）及其相关变体（Kamgarpour和Tomlin，2008，Li等，2018，Wu等，2018）和流言版本（Wan等，2018），以及迭代共识滤波器（ICF，Kamal等，2013）。 当共识步骤的数量趋于无穷大时，这些滤波器恢复了最优的集中式性能，但不保持局部估计的一致性。 为了解决这个问题，Battistelli等人（2015）的混合CM和CI（HCMCI）滤波器在先验估计和新测量上提出了双重共识迭代，从而实现了错误稳定性和任意数量的共识步骤的一致性。 最后，在分布式优化的视角下，Ryu和Back（2019）推导出了一个CI滤波器，该滤波器收敛到最优的集中式估计。

受到文献中完整理论结果缺乏的启发，本文探讨了共识滤波器的一些基本属性，即（i）当共识步骤数量增加时收敛到最优估计；（ii）协方差矩阵交换对性能及相关稳定性问题的影响；（iii）计算达到错误稳定所需的最小共识步骤数。 这种分析突出了适用于更一般系统类别的基本限制和权衡。

以下是论文的贡献和创新的总结：

（1）我们描述了两种CE滤波器。在简单的一种中（分布式卡尔曼滤波器，DKF），只交换估计值。在另一种（稳态修改的分布式卡尔曼滤波器，SMDKF）中，还交换协方差矩阵。通过仿真，我们展示了SMDKF产生的性能与CM滤波器相同，从而建立了CE和CM共识滤波器之间的等价性。

（2）我们对这些滤波器进行了完整的理论分析：稳定性和性能以及它们与共识步骤数量的依赖关系。由于我们表明文献中提出的算法没有一个在只有一个共识步骤时具有可接受的性能，我们认为在实践中，这个结果比仅仅建立任意数量的共识步骤的错误的稳定性更为重要。

（3）本文分析的一个突出而新的结果是，对于大量的共识步骤，仅交换估计值的简单算法趋向于最优的集中式估计，类似于连续时间情况（Battilotti等人，2020）。

（4）我们证明了，与预期相符，交换协方差矩阵的算法减少了估计误差均方稳定所需的最小共识步骤数。

（5）我们证明了，对于静态网络，可以分布式计算出实现稳定所需的最小共识步骤数。

该问题在第2节中形式化。DKF及其属性是第3节的对象。我们在第4节考虑了有向图，在第5节考虑了确定性情况。第6节介绍并研究了SMDKF。在第7节，针对一个边缘稳定和一个不稳定的系统，我们通过仿真对几种分布式共识滤波器进行了比较。这个比较验证了理论分析，并突显了现有方法的共同局限性。

📚2 运行结果

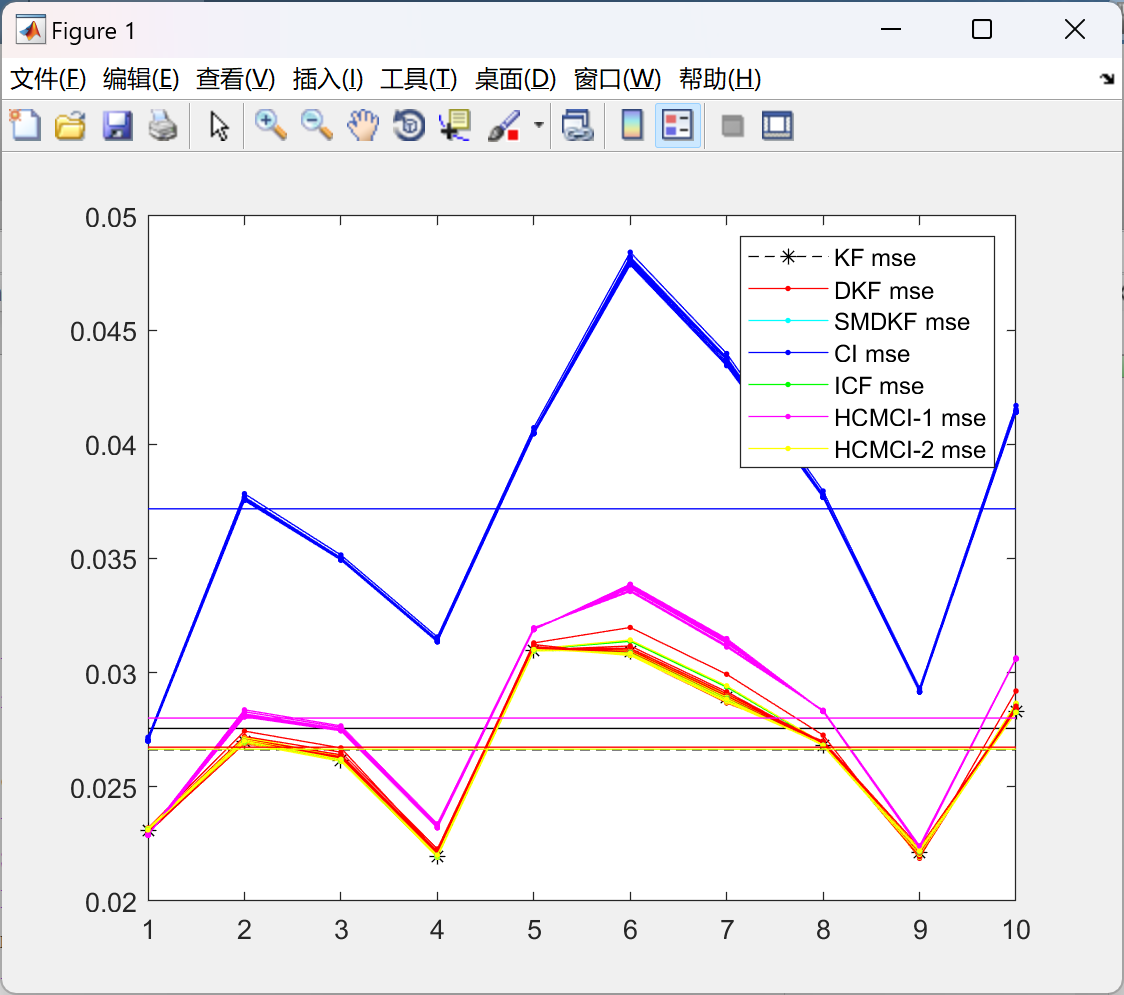
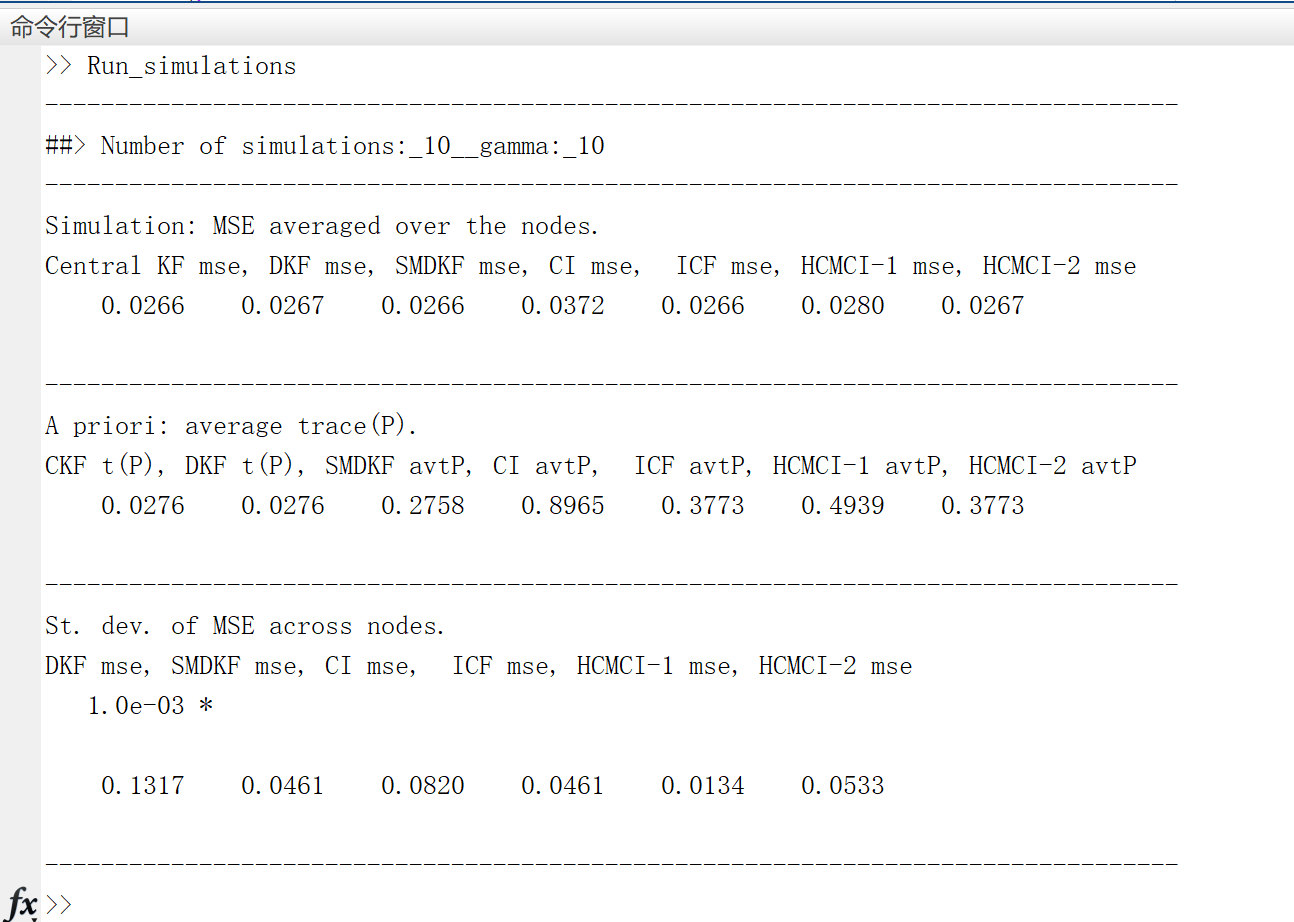
主函数代码：

%% Simulation script for:
% - DKF  (stationary, no exchange of matrices, single consensus cycle)
% - SMDKF  (information form, exchange of matrices offline, stationary)
% - ICF    [Kamal, 2013]
% - CI_filter (CIKF)
% - HCMCI-1 [Battistelli, 2015]
% - HCMCI-2 [Battistelli, 2015]
% - centralized Kalman Filter 
% rev 24.09.20 Filippo Cacace
%% initialize system & graph
init_ADKF;
%============================================
% Number of simulations
nsim= 1e1; %###
%============================================
% IMPORTANT: number of consensus iterations
gamma= 1e1; 
%====================================================================
% IMPORTANT: weight matrix for DKF, SMDKF
pig= max(diag(Lap)); % best uniform choice
%============================================
mseK= zeros(nsim,1);
mseA= zeros(nsim,N);    % DKF filter 
mseD= zeros(nsim,N);    % SMDKF filter
mseC= zeros(nsim,N);    % CIKF
mseICF= zeros(nsim,N);  % ICF, consensus on measurements filter
mseH1= zeros(nsim,1);   % HCMCI-1 filter
mseH2= zeros(nsim,1);   % HCMCI-2 filter
tra= round(tf/5); % transient
tp= zeros(1,N);

%% Main simulation cycle
for i=1:nsim
    [x,yN,ytot]= sistemaN(N,A,B,Q,qi,Ctot,Rtot,Ex0,Psix0,uk,tf,seed+i);
    [t,xh,Kf,P]= KF(A,B,Ctot,Q,Rtot,Ex0,Psix0,uk,tf,ytot);
    [~,xha,K,Pinf]= DKF(A,B,Ctot,Q,Rtot,Ci,Ri,N,Lap,qi,pig,gamma,Ex0,uk,tf,ytot);
    [~,xhd,PDKF,ZigD]= SMDKF(A,B,Q,Ci,Ri,N,Lap,qi,pig,gamma,Ex0,uk,tf,ytot); 
    [~,xhc,Omega]= CI_filter(A,B,Q,Ci,Ri,N,Lap,qi,gamma,Ex0,Psix0,uk,tf,ytot);
    [~,xhicf,Ji]= ICF_filter(A,B,Q,Ci,Ri,N,Lap,qi,gamma,Ex0,Psix0,uk,tf,ytot);
    [~,xhh1,Omegah1]= HCMCI1_filter(A,B,Q,Ci,Ri,N,Lap,qi,gamma,Ex0,Psix0,uk,tf,ytot);
    [~,xhh2,Omegah2]= HCMCI2_filter(A,B,Q,Ci,Ri,N,Lap,qi,gamma,Ex0,Psix0,uk,tf,ytot);
     % errors, without transient
     mseK(i)= mean(sum((x(:,tra:end)- xh(:,tra:end)).^2)); 
     for j=1:N
         mseA(i,j)= mean(sum((x(:,tra:end)- squeeze(xha(:,j,tra:end))).^2));
         mseD(i,j)= mean(sum((x(:,tra:end)- squeeze(xhd(:,j,tra:end))).^2));
         mseC(i,j)= mean(sum((x(:,tra:end)-xhc(:,tra:end,j)).^2));
         mseICF(i,j)= mean(sum((x(:,tra:end)-xhicf(:,tra:end,j)).^2));
         mseH1(i,j)= mean(sum((x(:,tra:end)-xhh1(:,tra:end,j)).^2));
         mseH2(i,j)= mean(sum((x(:,tra:end)-xhh2(:,tra:end,j)).^2));         
     end
end % for
tC= 0;
tH1= 0;
tH2= 0;
tICF= 0;
tIDKF= 0;
for i=1:N
    tC= tC + trace(inv(Omega((i-1)*n+1:i*n,:)));
    tICF= tICF+ trace(inv(Ji{i}));
    tIDKF= tIDKF+ trace(PDKF(:,(i-1)*n+1:i*n));
    tH1= tH1 + trace(inv(Omegah1((i-1)*n+1:i*n,:)));
    tH2= tH2 + trace(inv(Omegah2((i-1)*n+1:i*n,:)));
end

%% plot MSE
figure(1);
pkf=plot(1:nsim,mseK,'k*--');
hold on;
    % plot a priori error variance
plot(1:nsim,trace(P)*ones(1,nsim),'k-');
plot(1:nsim,mean(mseK)*ones(1,nsim),'k--');
for j=1:N
    padkf= plot(1:nsim,mseA(:,j),'r.-');    % DKF filter
    pidkf= plot(1:nsim,mseD(:,j),'c.-');    % SMDKF filter
    pcf= plot(1:nsim,mseC(:,j),'b.-');      % CI filter
    picf= plot(1:nsim,mseICF(:,j),'g.-');   % ICF filter
    phcmci1= plot(1:nsim,mseH1(:,j),'m.-'); % HCMCI-1 filter
    phcmci2= plot(1:nsim,mseH2(:,j),'y.-'); % HCMCI-2 filter
end
plot(1:nsim,mean(mean(mseA))*ones(1,nsim),'r-');
plot(1:nsim,mean(mean(mseD))*ones(1,nsim),'c-');
plot(1:nsim,mean(mean(mseC))*ones(1,nsim),'b-');
plot(1:nsim,mean(mean(mseICF))*ones(1,nsim),'g-');
plot(1:nsim,mean(mean(mseH1))*ones(1,nsim),'m-');
plot(1:nsim,mean(mean(mseH2))*ones(1,nsim),'y-');
legend([pkf, padkf, pidkf, pcf, picf, phcmci1,phcmci2],...
    'KF mse','DKF mse','SMDKF mse','CI mse','ICF mse','HCMCI-1 mse','HCMCI-2 mse');
saveas(gcf, '../results/mse.png')
disp('---------------------------------------------------------------------------------');
disp(strcat('##> Number of simulations:_',num2str(nsim),'__gamma:_',num2str(gamma)));
disp('---------------------------------------------------------------------------------');
disp('Simulation: MSE averaged over the nodes.')
disp('Central KF mse, DKF mse, SMDKF mse, CI mse,  ICF mse, HCMCI-1 mse, HCMCI-2 mse');
mK= mean(mseK);
mA= mean(mseA);
mID= mean(mseD);
mC= mean(mseC);
mICF= mean(mseICF);
mH1= mean(mseH1);
mH2= mean(mseH2);
disp([mK, mean(mA), mean(mID), mean(mC), mean(mICF), mean(mH1), mean(mH2)]);
disp('---------------------------------------------------------------------------------');
disp('A priori: average trace(P).');
disp('CKF t(P), DKF t(P), SMDKF avtP, CI avtP,  ICF avtP, HCMCI-1 avtP, HCMCI-2 avtP');
disp([trace(P), trace(Pinf), mean(tIDKF), mean(tC), mean(tICF), mean(tH1), mean(tH2)]);
disp('---------------------------------------------------------------------------------');
disp('St. dev. of MSE across nodes.');
disp('DKF mse, SMDKF mse, CI mse,  ICF mse, HCMCI-1 mse, HCMCI-2 mse');
disp([std(mA), std(mID), std(mC), std(mICF), std(mH1), std(mH2)]);
disp('---------------------------------------------------------------------------------');
out_p=[gamma, trace(P), mK,...
    mean(mA), mean(mID), mean(mC), mean(mICF), mean(mH1), mean(mH2),...
    std(mA), std(mID), std(mC), std(mICF), std(mH1), std(mH2)];

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、文章下载